《固体物理学》课程教学课件（PPT讲稿）Chapter 7 The electronic theory of metal（supplement - Sommerfield expansion）

7-1 supplement:Sommerfield expansion Set O(E)is continuously diffrentiated between (-co,+o), (0)=0,and lime afEy≥IfkeT<Er, prove that 1-r(E)0'(e)证=Q(e,)+石k,7Q'(E,) where f(E)=- F-D function E-EE

7-1 supplement: Sommerfield expansion Set Q(E) is continuously diffrentiated between（-，+）， Q(0)＝0 ，and ，α>0。If kBT << EF， prove that lim 0 ( ) E E e Q E − → = ( ) ( ) ( ) ( ) ( ) 2 2 0 d 6 F B F I f E Q E E Q E k T Q E   =  +    where ( ) 1 exp 1 F B f E E E k T =   −   +   F－D function

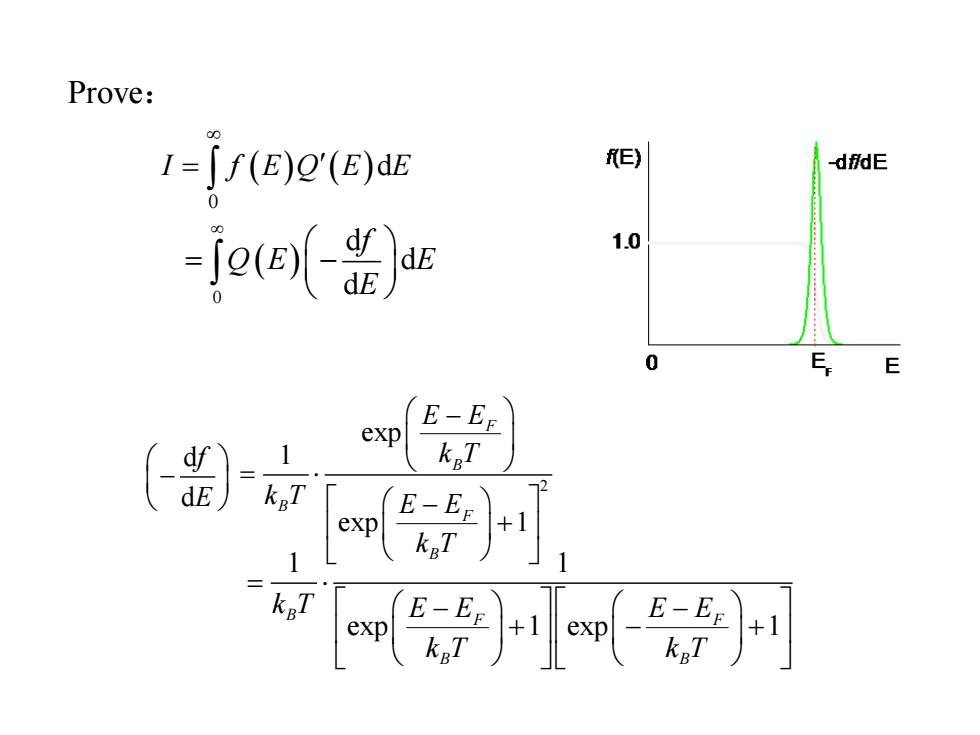
Prove: I=Jf(E)0(E)dE f(E) -dfdE -j()r 1.0 0 E E E-Eg exp kgT kgT exp E-EE +1 kgT kgT

Prove： ( ) ( ) 0 I f E Q E Ed  =   ( ) 0 d d d f Q E E E    = −     d d f E     −   2 exp 1 exp 1 F B B F B E E k T k T E E k T   −     =      −     +     1 1 exp 1 exp 1 B F F B B k T E E E E k T k T =          − −         + − +        

We find that (-df7dE)is a even function of (E-E), the value of (-dfdE)is mainly focused nearby the scope of E-EF~kBT,if E-EFl>n kBT,the value of the function is approaching 0 rapidly,similar to the function of δ So,the contribution to the integral is mainly focused in the small scope of E~Er,because Er>>kBT,the lower limit of the integral is replaced by -oo from 0,and the integral value is supposed not to be changed. 1=joae

(-df/dE) is a even function of（E－EF）, the value of (-df/dE) is mainly focused nearby the scope of  E－EF  kBT，if  E－EF > n kBT，the value of the function is approaching 0 rapidly, similar to the function of δ So, the contribution to the integral is mainly focused in the small scope of E ~ EF，because EF >> kBT，the lower limit of the integral is replaced by -∞ from 0，and the integral value is supposed not to be changed. ( ) d d d f I Q E E E  −    = −     We find that

perform the Taylor expansion on O(E)nearby E=EE (E)=(E)+E)(E-E)+"(Er)(E-E)'+. =iee,〔}r+jQ(Ee-,〔ur +5Q(,6-R,{)c+ wherej()()

perform the Taylor expansion on Q(E) nearby E=EF ( ) ( ) ( )( ) ( )( ) 1 2 2! Q E Q E Q E E E Q E E E F F F F F = + − + − +   ( ) ( )( ) d d d d d d F F F f f I Q E E Q E E E E E E   − −      = − + − −            ( )( ) 2 d 1 d 2 d F F f Q E E E E E  −   + − − +        ( ) ( ) 0 d d d F F f I Q E E Q E E  −   = − =      where

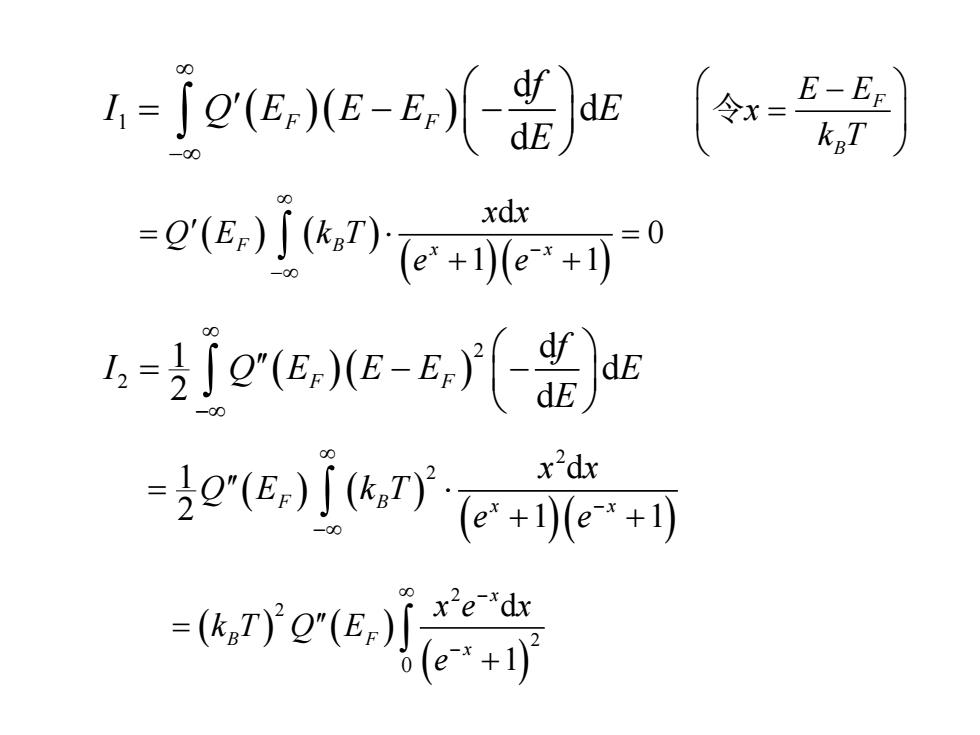
4-eec-￥s〔尝 -eie德可0 4=fQe,E-,（) g7可 xdx -i

( )( ) 1 d d d F F f I Q E E E E E  −   = − −       ( ) ( ) ( )( ) d 0 1 1 F B x x x x Q E k T e e −  − =  =  + +  F B E E x k T   −   =   令 ( )( ) 2 2 d 1 d 2 d F F f I Q E E E E E  −   = − −       ( ) ( ) ( )( ) 2 2 d 1 2 1 1 F B x x x x Q E k T e e −  − =   + +  ( ) ( ) ( ) 2 2 2 0 d 1 x B F x x e x k T Q E e − −  =  + 

Perform Taylor expansion 0-1(,on-e,-g 3 -旷ga,订r02a4ja -eryos+s+ -T（k,Q(E) 1,11 1-+3 π2 12 [f(E)0'(E)dEQ(E,)+石(，T)'Q(E,)

( ) ( ) ( )( 1 1 2 ) 2 3 ( )( )( ) 1 1 2! 3! n n n n n n     n − − − − − − − − − + = + − + + +  Perform Taylor expansion ( ) ( ) 2 2 2 3 2 0 1 2 3 4 x x x x B F I k T Q E x e e e e dx − − − −   = − + − +        ( ) ( ) 2 2 2 2 1 1 1 2! 1 2 3 4 B F k T Q E     = − + − +           ( ) ( ) 2 2 6 B F k T Q E  =  2 2 2 2 1 1 1 1 2 3 4 12  − + − +  = ( ) ( ) ( ) ( ) ( ) 2 2 0 d 6 F B F f E Q E E Q E k T Q E      + 

7-2 supplement:the calculation of systematical energy at T>0 (EE-CI E2 dE rw-e y'dy F;(o)I(j+1)exp(o) Rw- %>1

3 2 0 0 ( ) ( )d d 1 exp F B E U EN E f E E C E E E k T   = =   − +       0 0 0 0 0 1 2 0 0 2 0 d ( ) 1+exp(y-y ) ( ) ( 1)exp( ) ( 1) ( ) 1 ( 1) 6 j j j j j y y F y F y j y y j j F y j y   + =   +   +  + +    +    0 ( ) 2 −  y 0 y  1 7-2 supplement: the calculation of systematical energy at T>0

3 5 E2 2 Er>>kgT 1+exp E-Ee 门 +会j] .j T<<Eg/kg

3 5 2 2 2 0 2 5 d 1 - 5 8 1+exp F B F F B E E k T E E E E k T        +                  E k T F B  5 2 2 0 2 0 5 2 0 2 0 2( ) 5 5 1 1 5 24 8 2( ) 5 1 5 12 F B B F F F B F E k T k T E E E k T E             − +                          +           ( ) 5 3 0 2 2 2 2 2 0 2 2 2 0 0 2 5 1 5 12 4 F B F B F E m k T U E n k T U E           +                 = +     0 / T E k  F B

7-3 supplement:the DOS at Fermi surface 3 n 2 322 一k,=(3 2m .N(E)= 3 n 2 E

7-3 supplement: the DOS at Fermi surface ( ) 3 3 1 2 2 0 0 0 2 2 2 2 2 2 2 2 2 3 2 2 2 1 2 1 2 ( ) 2 2 2 1 1 3 2 3 2 F F F F F F F F m m k N E C E E m m m n n k k k k m          = = =          = = = 0 0 3 ( ) 2 F F n N E E  = ( ) 1 2 3 3 F k n = 