《固体物理学》课程教学课件（PPT讲稿）Chapter 3 Interatomic Bonding 3.3 The cohesive energy for ionic crystal

3.3 The cohesive energy for ionic crystal For NaCl,the interaction energy for two ionics could be written a尽无法显示该国片， u(r)=± e+ b 4πEor For crystal with N atoms,the interactionenergy could be wy Positive for the same charge,and negative for opposite charge If 1 The shortest distance between two ionics,taken as the unit distance U=-N e 4πEo6j

3.3 The cohesive energy for ionic crystal For NaCl, the interaction energy for two ionics could be written as 2 0 ( ) 4 ij n e b u r  r r =  + 0 ij ij 2 j 1 (2 ) 2 4 n e b U N  r r   =  +        Positive for the same charge, and negative for opposite charge If ij ij 0 r a r = The shortest distance between two ionics, taken as the unit distance 0 r 2 0 0 0 1 1 4 n n j j ij ij e b U N  r a r a   = −  −         For crystal with N atoms, the interaction energy could be

Let's take a,B,are constants for crystals,dependent of the crystal structure,where Madelung constant B U=-N Qe2 4π8% The equilibrium constant could be determined by B、 ae 4πn 4πEonB ae2 The energy at stable state

2 0 0 0 4 n e B U N r r     = − −     2 0 0 0 1 1 4 e U N r n     = − −     0 0 2 2 1 0 d 0 d 4 n r r U e nB N r r r   +   = − − + =     2 1 0 0 1 1 0 0 2 4 4 n n e B r n nB r e     − − =   =     The energy at stable state 1 j ij a  =   n j ij b B a Let’s take =  are constants for crystals, dependent of the crystal structure，where Madelung constant The equilibrium constant could be determined by

*For a given crystal,the Madelung constant could be calculated *ionic distance ro could be determined by the XRD *the value of n could be determined by the experimental investigation of elastic modulus K All of these results show that the experimental results are consistent with the theoretical values,which supports the fact that the interaction between positive and negative ionics should be responsible for the ionic bonding

★For a given crystal, the Madelung constant could be calculated ★ionic distance r0 could be determined by the XRD ★the value of n could be determined by the experimental investigation of elastic modulus K All of these results show that the experimental results are consistent with the theoretical values, which supports the fact that the interaction between positive and negative ionics should be responsible for the ionic bonding

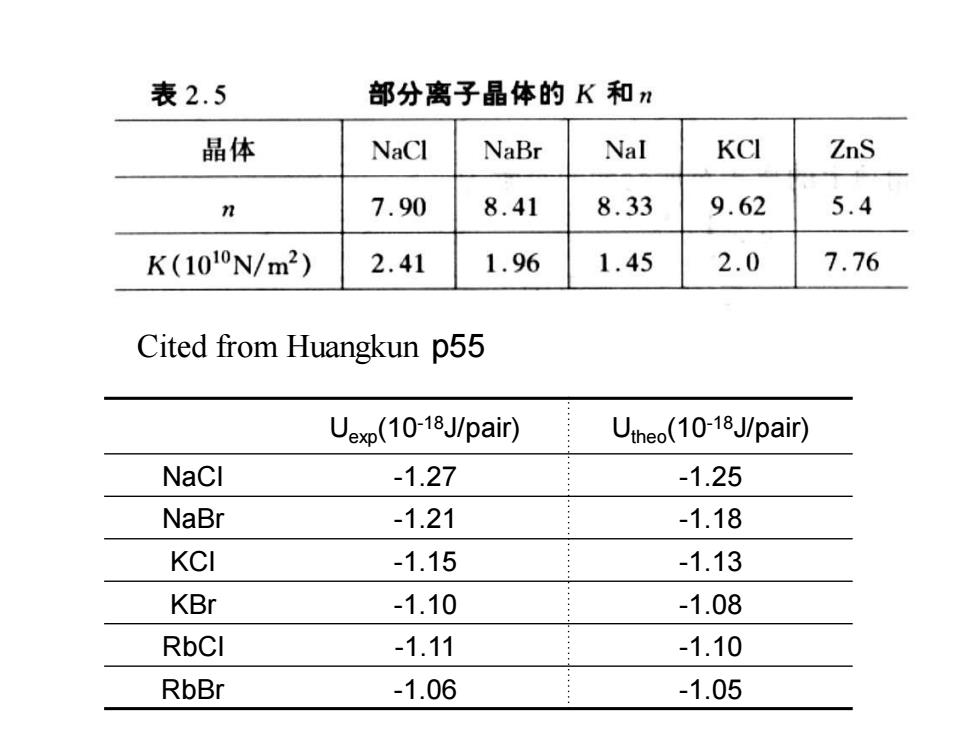
表2.5 部分离子晶体的K和n 晶体 NaCl NaBr Nal KCI ZnS n 7.90 8.41 8.33 9.62 5.4 K(1010N/m2) 2.41 1.96 1.45 2.0 7.76 Cited from Huangkun p55 Uexp(10-18J/pair）) Utheo(10-1J/pair) NaCl -1.27 -1.25 NaBr -1.21 -1.18 KCI -1.15 -1.13 KBr -1.10 -1.08 RbCI -1.11 -1.10 RbBr -1.06 -1.05

Uexp(10-18J/pair) Utheo(10-18J/pair) NaCl -1.27 -1.25 NaBr -1.21 -1.18 KCl -1.15 -1.13 KBr -1.10 -1.08 RbCl -1.11 -1.10 RbBr -1.06 -1.05 Cited from Huangkun p55

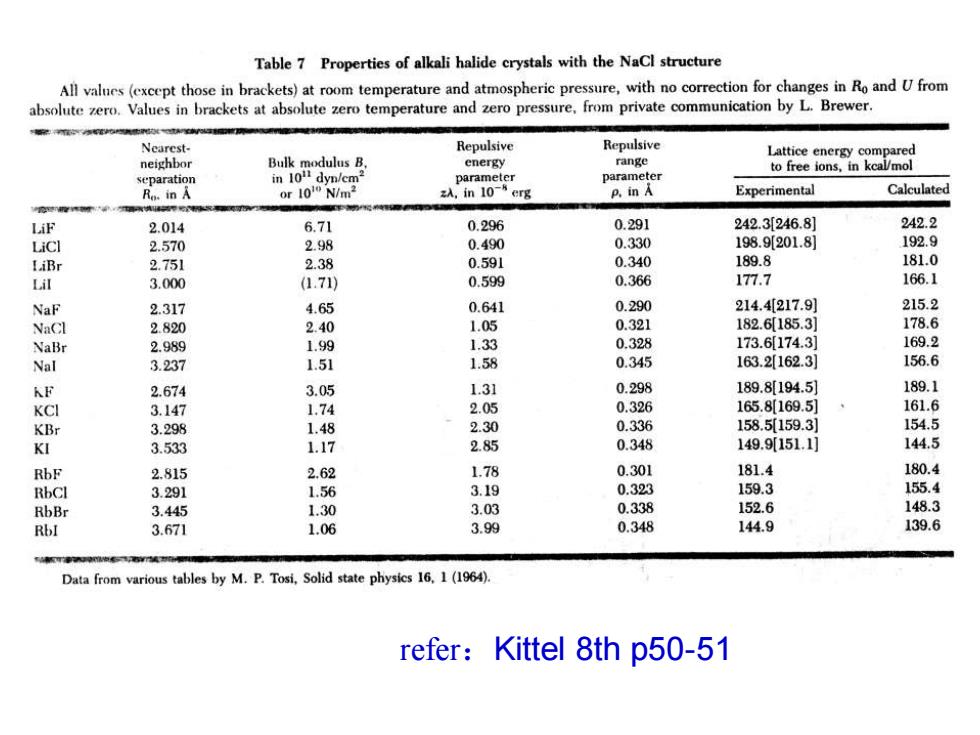
Table 7 Properties of alkali halide crystals with the NaCl structure All values(except those in brackets)at room temperature and atmospheric pressure,with no correction for changes in Ro and U from absolute zero.Values in brackets at absolute zero temperature and zero pressure,from private communication by L.Brewer. Nearest- Repulsive Repulsive Lattice energy compared neighbor Bulk modulus B. energy range to free ions,in kcal/mol in 1011 dyn/em? parameter parameter or 1010 N/m2 zA,in 10-"erg p.in A Experimental Calculated LiF 2.014 6.71 0.296 0.291 242.3[246.8] 242.2 LiC] 2.570 2.98 0.490 0.330 198.9[201.8] 192.9 LiBr 2.751 2.38 0.591 0.340 189.8 181.0 Lil 3.000 (1.71) 0.599 0.366 177.7 166.1 NaF 2.317 4.65 0.641 0.290 214.4[217.9 215.2 NaCl 2.820 2.40 1.05 0.321 182.6185.3] 178.6 NaBr 2.989 1.99 1.33 0.328 173.6174.3] 169.2 Nal 3.237 1.51 1.58 0.345 163.2162.3] 156.6 KF 2.674 3.05 1.31 0.298 189.8[194.5] 189.1 KCI 3.147 1.74 2.05 0.326 165.8169.5] 161.6 KBr 3.298 1.48 2.30 0.336 158.5[159.3] 154.5 KI 3.533 1.17 2.85 0.348 149.9151.1] 144.5 RbF 2.815 2.62 1.78 0.301 181.4 180.4 RbCl 3.291 1.56 3.19 0.323 159.3 155.4 RbBr 3.445 1.30 3.03 0.338 152.6 148.3 RbI 3.671 1.06 3.99 0.348 144.9 139.6 Data from various tables by M.P. Tosi, Solid state physics 16.1(1964) refer:Kittel 8th p50-51

refer：Kittel 8th p50-51

The relation between elastic modulus K and repulsive efficient n a'U sc: y=1 K=Vo Vo=yNi NaCl:Y=2 x=器=r器】 1 U K= 9YNr dr2 B= 4π8n d2U Nae2 (n-1) 4πe0 K= ae2 (n-1) n=1+ 72E2K 72π8oYT0 ae2

The relation between elastic modulus K and repulsive efficient n 0 2 0 2 ( )V U K V V  =  3 V Nr 0 0 =  sc: =1 NaCl: =2   0 2 2 0 1 d 9 d r U K  Nr r   =     ( ) ( ) 2 1 0 0 2 2 2 3 0 0 2 4 0 0 4 d 1 d 4 1 72 e n B r n U N e n r r e K n r        − = = − = − 4 0 0 2 72 1 r n K e    = + 2 2 2 2 2 U U r K V V V r V          = =             

The Lennard-Jones Potential j Contributions: The short range 1/r12 repulsive term The long range Dipole-dipole (including H-bonding) 1/attractive term Induced dipole London dispersion attraction u(r)/e : 0 : r/a 0 3

The Lennard-Jones Potential ( )                −      = 12 6 4 r r u r    The long range 1/r6 attractive term The short range 1/r12 repulsive term u(r)/ε r/σ 0 0 1 2 3 Contributions: Dipole-dipole (including H-bonding) Induced dipole London dispersion attraction ε

Interaction potential for atoms pair - a=480°，b=48o2,or:o 93 a 4b When there are N atoms or molecules in the crystal,the interaction energy should be: a The shortest distance between two atoms is ro,if= U(r）=2Nε

Interaction potential for atoms pair 6 12 ( ) a b u r r r = − + 12 6 u r( ) 4 r r          = −               6 12 a b = = 4 , 4 ,   1 2 6 , 4 b a a b     = =     or： When there are N atoms or molecules in the crystal, the interaction energy should be: 12 6 0 j j 4 2 N U r r               = −                          j The shortest distance between two atoms is r0 , if 0 r a r j j = 12 6 12 6 0 0 U r N ( ) 2 A A r r          = −               &

where are dependent of the crystal structures lattice summerary for three cubic Bravis lattices scc bec fee 8.40 12.25 14.45 6.20 9.11 12.13 Using equilibrium condition, aU(r) =0 6=0 2A2 ☐1.09g Or Ao The majority of molecular crystals possess fec structure.we can introduce the corresponding data into the above expression,and we can find that o represent the radius for atomic core repulsion At equilibrium state,the energy should be: U(6) 40= N =-8.66 reflects the binding energy For fcc structure,the energy of an atom on average U6)=-N82Ag

0 U r N ( ) = −   2 6 12 A 2A At equilibrium state, the energy should be: 0 0 ( ) 8.6 U r u N = = −  For fcc structure, the energy of an atom on average ε reflects the binding energy

At equilibrium state,the elastic modulus for fcc structure K- 4cAg =758 √2yo3A Solid binding energy for inert gas elements uexp (eV/atom) uthe(eV/atom) Ne -0.02 -0.027(-0.019) Ar -0.08 -0.089(-0.080) Kr -0.11 -0.120(-0.113) Xe -0.17 -0.172 Referred from huangkun p70

uexp (eV/atom) uthe (eV/atom) Ne -0.02 -0.027 (-0.019) Ar -0.08 -0.089 (-0.080) Kr -0.11 -0.120 (-0.113) Xe -0.17 -0.172 Referred from huangkun p70 Solid binding energy for inert gas elements 3 3 4 75 K     = 5 2 3 2 6 12 A 2 A At equilibrium state, the elastic modulus for fcc structure