
4-1 supplement Thermal Expansion of Glass Thermal expansion determines if a glass will be shock resistant,able to withstand high thermal stresses Small thermal expansion coefficient leads to high thermal shock resistance Large thermal expansion leads to low thermal shock resistance Most materials expand as they are heated Refractory metals and ceramics-Expand less Polymers-Expand more Some materials expand very little SiO2 glass;b-spodumene,Li2O.Al2O3.4SiO2 Complex systems with more than one material must have matched or compensated thermal expansions
4-1 supplement : Thermal Expansion of Glass • Thermal expansion determines if a glass will be shock resistant, able to withstand high thermal stresses • Small thermal expansion coefficient leads to high thermal shock resistance • Large thermal expansion leads to low thermal shock resistance Most materials expand as they are heated Refractory metals and ceramics-Expand less Polymers-Expand more Some materials expand very little SiO2 glass; b-spodumene, Li2O.Al2O3 .4SiO2 Complex systems with more than one material must have matched or compensated thermal expansions
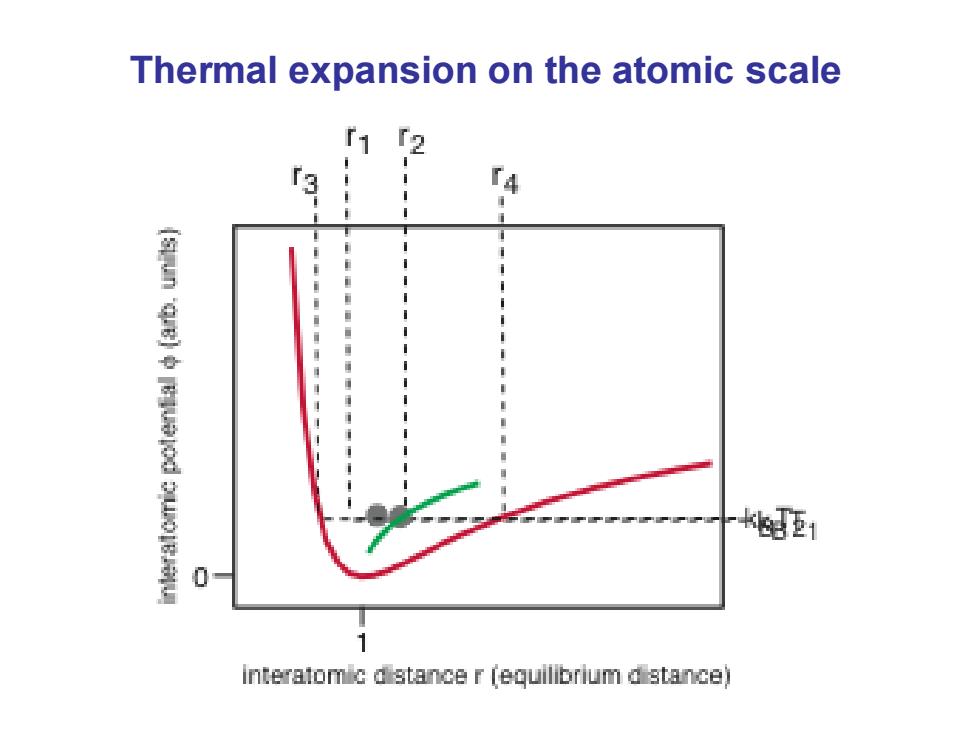
Thermal expansion on the atomic scale f1 更1 interatomic dstance r (equilibrium d stance)
Thermal expansion on the atomic scale
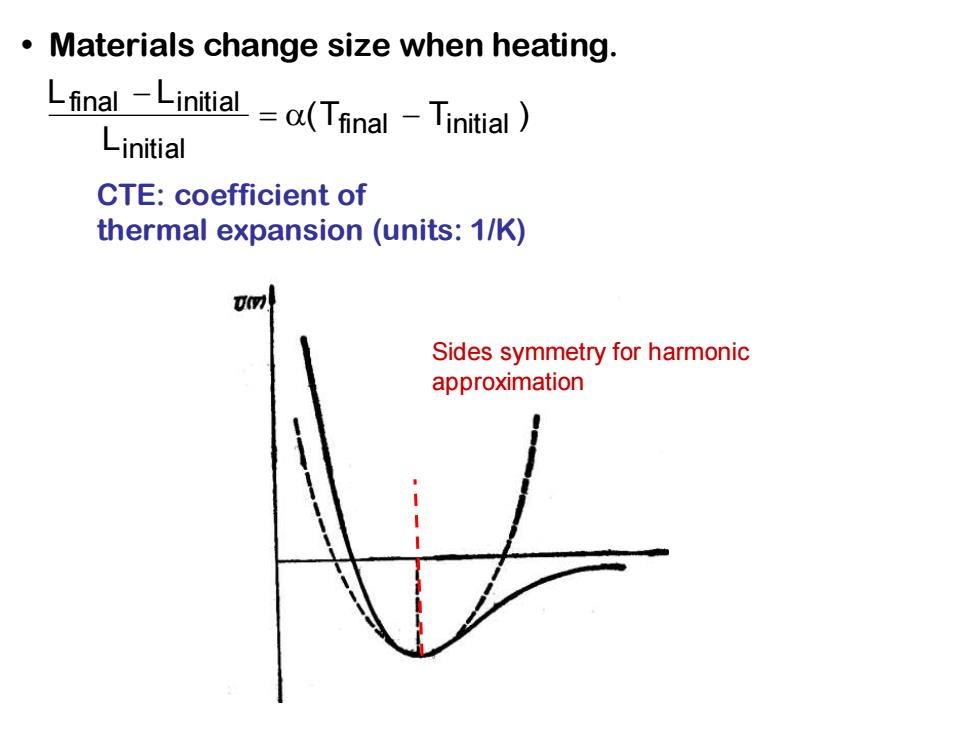
Materials change size when heating. Lfinal -Linitial =a(Tfinal-Tinitial Linitial CTE:coefficient of thermal expansion (units:1/K) Uov) Sides symmetry for harmonic approximation
• Materials change size when heating. Lfinal − Linitial Linitial = (Tfinal − Tinitial ) CTE: coefficient of thermal expansion (units: 1/K) Sides symmetry for harmonic approximation
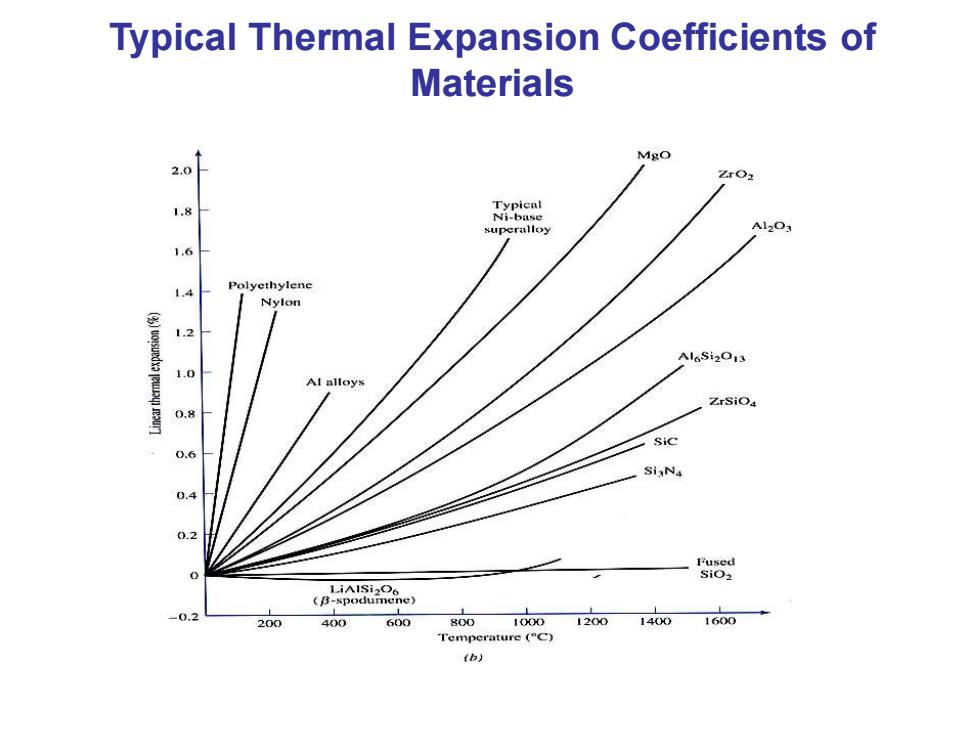
Typical Thermal Expansion Coefficients of Materials Mgo 20 1.8 Ni-base superalloy A12O3 1.6 1.4 Polyethylene Nylon (wotsuedxa eu 1.2 Al alloys ZrSiO 0.8 Sic 0.6 SiaNa 0.4 0.2 LiAlSi2O6 (B-spodumene) 0.2 200 400 600 800 1000 1200 1400 1600 Temperature (C) (b)
Typical Thermal Expansion Coefficients of Materials
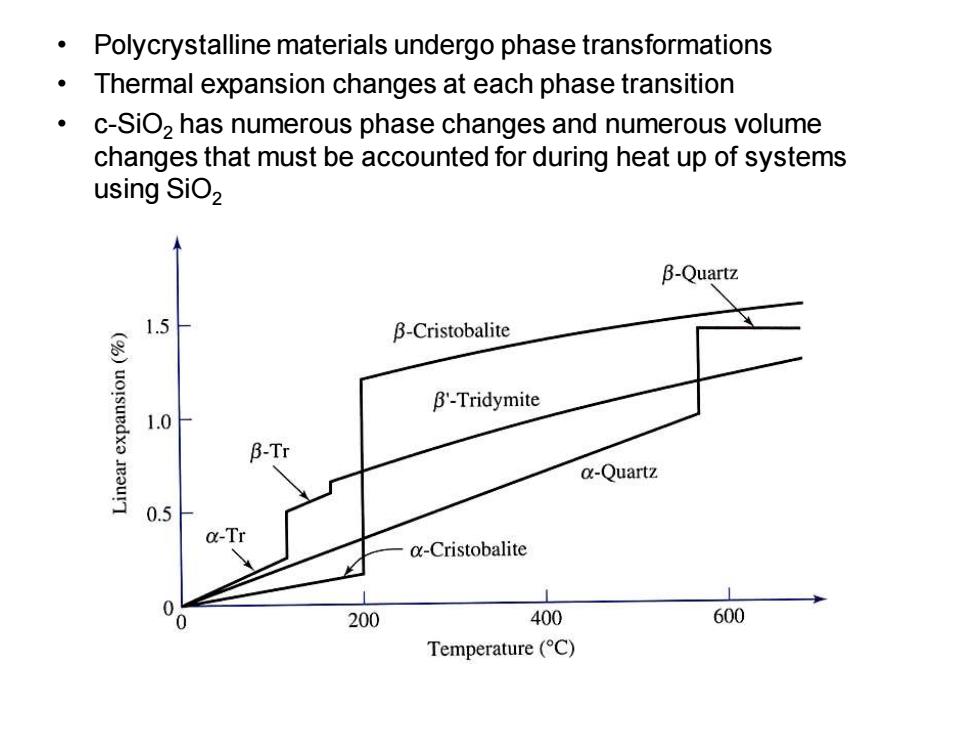
Polycrystalline materials undergo phase transformations Thermal expansion changes at each phase transition 。 c-SiO,has numerous phase changes and numerous volume changes that must be accounted for during heat up of systems using SiO2 B-Quartz 1.5 B-Cristobalite B'-Tridymite 1.0 B-Tr a-Quartz 0.5 a-Tr @-Cristobalite 0 200 400 600 Temperature (C)
• Polycrystalline materials undergo phase transformations • Thermal expansion changes at each phase transition • c-SiO2 has numerous phase changes and numerous volume changes that must be accounted for during heat up of systems using SiO2
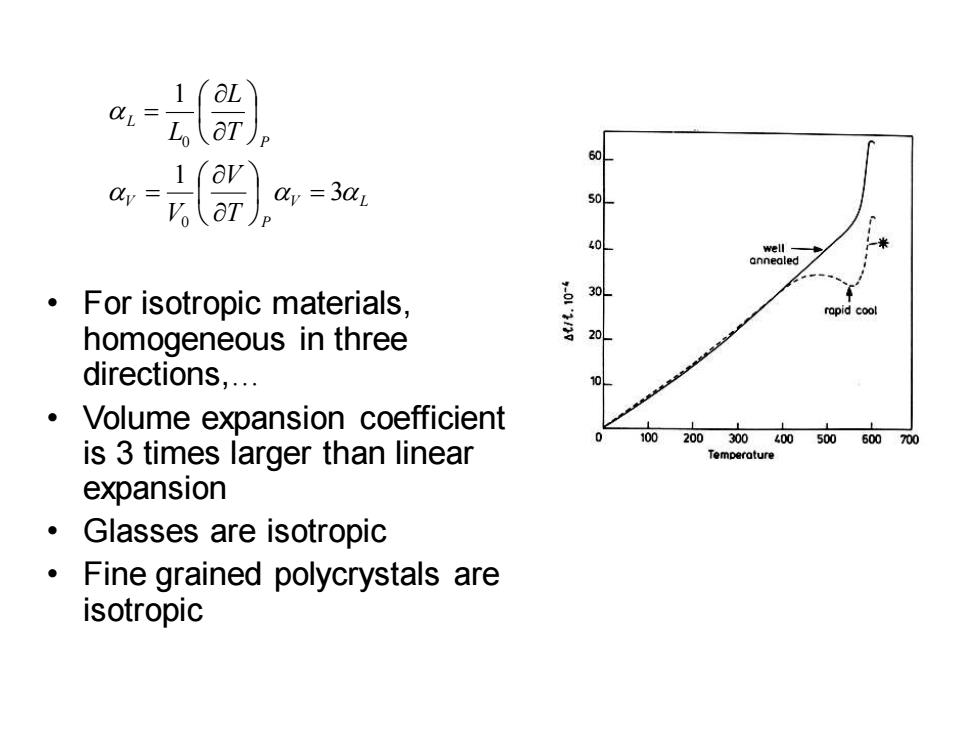
aL 1 =3z 50 40 well annealed For isotropic materials, 30 rapid cool homogeneous in three 20 directions,. Volume expansion coefficient 100 200300400500600700 is 3 times larger than linear Temperature expansion Glasses are isotropic Fine grained polycrystals are isotropic
• For isotropic materials, homogeneous in three directions,. • Volume expansion coefficient is 3 times larger than linear expansion • Glasses are isotropic • Fine grained polycrystals are isotropic V L P V P L T V V T L L 3 1 1 0 0 = = =

Thermal Expansion of Alkali Borate Glasses 27 oLi 口Ne OK 2 Rb NOISNYdX3 20 40 60 100 MOL%R,0 Addition of alkali modifier decreases thermal expansion coefficient in alkali borate glasses Modifier in low alkali borate glasses,cross links glass structure Creation of tetrahedral borons Adding bonds to boron,increasing connectivity of network Strengthening the network Rigidity of the glassy network increases Thermal expansion decreases with modifier
Thermal Expansion of Alkali Borate Glasses • Addition of alkali modifier decreases thermal expansion coefficient in alkali borate glasses • Modifier in low alkali borate glasses, cross links glass structure • Creation of tetrahedral borons • Adding bonds to boron, increasing connectivity of network • Strengthening the network • Rigidity of the glassy network increases • Thermal expansion decreases with modifier

4-2 supplement Morse shows another expression for the potential p(r) Any real crystal resists compression to a smaller ev) volume than its equilibrium value more strongly 10 than expansion due to a larger volume. 12 ao a(T)=a+δ Peter Bruesch Phonons:Theory and Experiments I P154
4-2 supplement : Morse shows another expression for the potential Peter Bruesch Phonons:Theory and Experiments Ⅰ P154 Any real crystal resists compression to a smaller volume than its equilibrium value more strongly than expansion due to a larger volume. 0 a T a ( ) = +

Morse potential 4r)=D[1-e-了 D deionization, 2>0 Expand it: u(a+6)=4(a)+ dr + Defined as 0 0,at equilibrium point Harmonic term anharmonic term A+后8+ ,1 h,64+. 24 64+
0 2 ( ) ( ) 1 r a u r D e− − = − D deionization, >0 Expand it: 0 0 0 2 3 2 3 0 0 2 3 2 3 4 0 0 0 d 1 d 1 d ( ) ( ) d 2 d 3! d 1 1 1 2 6 24 a a a u u u u a u a r r r g h + = + + + = + + + 0 4 4 4 1 d 4! d a u r + + Defined as 0 0, at equilibrium point Harmonic term Morse potential anharmonic term

B,80,h are force constant, Only consider the cubic term: B。=222D>0 1 80=-6λ3D0 0 □ Harmonic term anharmonic term Based on the Boltzman statistics With no cubic term u +0 δekrdδ 80=0,6=0 δ= +00 2 With cubic term,thermal expansion occurs and the coefficient is a constant 1dδ Deviation from the equilibrium point goke a,dT 2ao
are force constant, 0 0 0 , , g h 2 0 3 0 4 0 2 0 6 0 14 0 D g D h D = = − = Only consider the cubic term: 2 3 0 0 0 1 1 ( ) 2 6 u a g + + Harmonic term anharmonic term Based on the Boltzman statistics 0 2 0 d 1 2 d u kT u B kT e g k T e + − − + − − = = − Deviation from the equilibrium point 0 g = = 0, 0 With no cubic term 0 2 0 0 0 1 d d 2 B g k a T a = − With cubic term, thermal expansion occurs and the coefficient is a constant