《固体物理学》课程教学课件（PPT讲稿）Chapter 5 band theory 5.3 Nearly Free Electron 5.4 BZ and energy bands

5.3 Nearly Free Electron The potential of electron is weaker than the kinetics of electron, and the motion could be seen as almost free.So,free electron motion is supposed to be the zeroth order approximation and the influence of periodical potential is regarded as the perturbation.at the same time,the motion must also obeys the symmetry condition This model is called empty lattice model. potential U ion core 1D periodical potential field for the electrons in the crystal

5.3 Nearly Free Electron The potential of electron is weaker than the kinetics of electron, and the motion could be seen as almost free. So, free electron motion is supposed to be the zeroth order approximation and the influence of periodical potential is regarded as the perturbation. at the same time, the motion must also obeys the symmetry condition. This model is called empty lattice model. 1D periodical potential field for the electrons in the crystal

for the case of 1D,the state function and energy for the empty lattice model should be: 1 2m where 0 indicates the solution with no perturbation.The relation between energy and wave vector is parabolic.Considering the requirement of symmetry,it is splitted into many parts.The energy of any two equivalent points could be the same by translatingthe integer multi of reciprocal vector G= a The values ofk for free e is not limited and the energy is continuous

for the case of 1D, the state function and energy for the empty lattice model should be： 2 2 (0) (0) 1 , 2 ik r k k k e E L m   = = where 0 indicates the solution with no perturbation. The relation between energy and wave vector is parabolic. Considering the requirement of symmetry, it is splitted into many parts. The energy of any two equivalent points could be the same by translating the integer multi of reciprocal vector 2 Gh a  = The values of k for free e is not limited and the energy is continuous

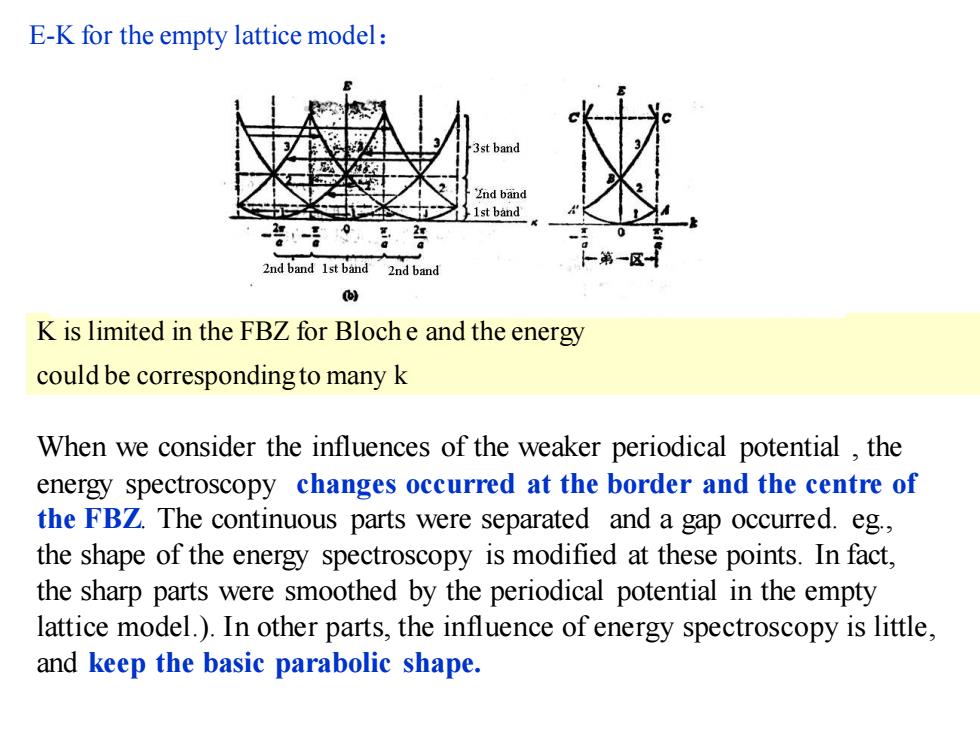
E-K for the empty lattice model: End band Ist band 24 2nd band Ist band 2nd band K is limited in the FBZ for Bloche and the energy could be corresponding to many k When we consider the influences of the weaker periodical potential,the energy spectroscopy changes occurred at the border and the centre of the FBZ.The continuous parts were separated and a gap occurred.eg., the shape of the energy spectroscopy is modified at these points.In fact, the sharp parts were smoothed by the periodical potential in the empty lattice model.).In other parts,the influence of energy spectroscopy is little, and keep the basic parabolic shape

E-K for the empty lattice model： K is limited in the FBZ for Bloch e and the energy could be corresponding to many k When we consider the influences of the weaker periodical potential , the energy spectroscopy changes occurred at the border and the centre of the FBZ. The continuous parts were separated and a gap occurred. eg., the shape of the energy spectroscopy is modified at these points. In fact, the sharp parts were smoothed by the periodical potential in the empty lattice model.). In other parts, the influence of energy spectroscopy is little, and keep the basic parabolic shape

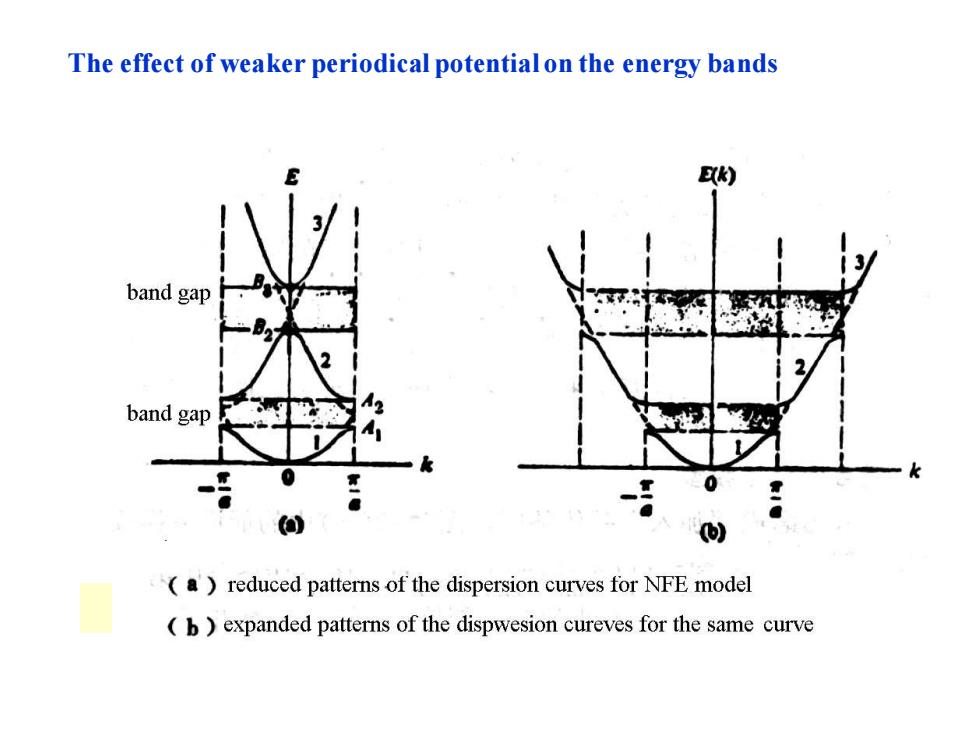
The effect of weaker periodical potential on the energy bands band gap band gap (a)reduced patterns of the dispersion curves for NFE model b expanded patterns of the dispwesion cureves for the same curve

The effect of weaker periodical potential on the energy bands

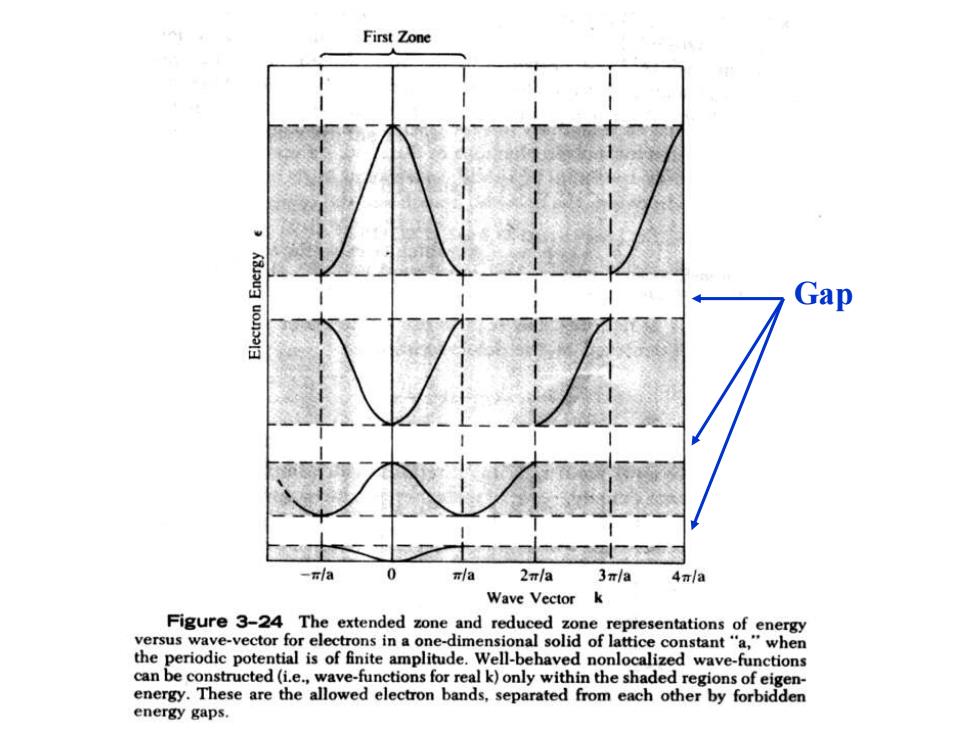
First Zone Gap -/a la2πla3πla4/a Wave Vector k Figure 3-24 The extended zone and reduced zone representations of energy versus wave-vector for electrons in a one-dimensional solid of lattice constant"a,"when the periodic potential is of finite amplitude.Well-behaved nonlocalized wave-functions can be constructed(i.e.,wave-functions for real k)only within the shaded regions of eigen- energy.These are the allowed electron bands,separated from each other by forbidden energy gaps

Gap

Perturbation method calculation:a 1D crystal L=Na 「-器e=vd U(x)=U(x+a) a is the lattice constant Fourier expansion: U(x)=U,+∑U,exp ,2πx a where U-U()dk average potential U =constant v.(es U minute term Potential is real term,not complex,so U(x)=U(x),UU

U x U x a ( ) = + ( ) a is the lattice constant Fourier expansion： ( ) 0 0 2 exp n n nx U x U U i a     = +      where ( ) 0 0 1 L U U x dx L =  —— average potential =constant ( ) 0 1 2 exp L n nx U U x i dx L a    = −     L Na = Un minute term Potential is real term, not complex，so U(x)=U* (x)， Un * =U-n 。 Perturbation method calculation: a 1D crystal ( ) ( ) ( ) 2 2 2 2 d U x x E x m dx     − + =     U

5.3.1.Nondegenerate perturbation H4=E(k)4H=- h2 d2 mdr+U(x) 品+-. 、 =H。+H n≠( H h2 d2 2m dx2 Zeroth order approximation r-22） Perturbationterm expand E(k)and v(k) E(k)=E0+E+E2+. 4=g0)+y0+y2)+

5.3.1. Nondegenerate perturbation ( ) H E k   k k = ( ) 2 2 2 d 2 d H U x m x = − + 2 2 2 0 0 0 d 2 exp 2 d n n nx U U i H H m x a     = − + + = +       2 2 0 0 2 d 2 d H U m x = − + Zeroth order approximation 0 2 exp n n nx H U i a      =      Perturbation term expand E(k) and (k) ( ) (0) (1) (2) E k E E E = + + +  k k k (0) (1) (2)     k k k k = + + + 

Substitute it in the Schrodinger equation Hw=E How+H'vEw+Eo How +Hv=EE+E HEZeroth order approximation 2k2 Energy eigenvalue Let Uo=0 2m = 1 The corresponding wave function e Orthogonal normalization: ∫yery9=k1k）=d The 1st order perturbation eq H"+Hy°=E0+Ey0

Substitute it in the Schrödinger equation (0) (0) (0) H E 0   k k k = (1) (0) (0) (1) (1) (0) H H E E 0     k k k k k k + = +  (2) (1) (0) (2) (1) (1) (2) (0) H H E E E 0      k k k k k k k k + = + +  Zeroth order approximation (0) (0) (0) H E 0   k k k = Energy eigenvalue 2 2 2 2 (0) 0 2 2 k k k E U m m = + = The corresponding wave function (0) 1 ikx k e L  = Orthogonal normalization： (0) (0) 0 L k k k k    dx k k    = =   The 1st order perturbation eq (1) (0) (0) (1) (1) (0) H H E E 0     k k k k k k + = +  Let U0=0

assume "-∑a"y9 ∑a"Ey0+Hy=E∑ap°+Ew° Lef-handed multiplicationrespectively and then integral aE0+Hk=Ega0+Eδ if k'=k E=H=∫*H'yk=kHlk) -e[Σ4，m2a产0 ifk≠k a E-E because E(1)=0,we need the second perturbation eq for the determination of perturbation energy

assume (1) (1) (0) k   = a (1) (0) (0) (0) (0) (1) (0) (1) (0) k k k k   a E H E a E     + = +  Left-handed multiplication respectively and then integral (0)  k   (1) (0) (0) (1) (1) k k k k k k k k k a E H E a E      + = +   if k’ = k (1) (0) (0) 0 L E H H dx k H k k kk k k    = = =     (1) 0 0 1 2 exp 0 L ikx ikx k n n nx E e U i e dx L a −       = =           if k’  k (1) (0) (0) k k k k k H a E E     = − because Ek (1)＝0，we need the second perturbation eq for the determination of perturbation energy

assume aSubstitute it into the second perturbation eq A=E”+-+a 2m E-E0 + 2mU, 2m 以1时+名” K'=k+2πn a 1得

assume (2) (2) (0) k   = a Substitute it into the second perturbation eq 2 2 2 (0) (2) (0) (0) 2 k k k k k k k k k k H E E E m E E    = + = + −  2 2 2 2 0 2 2 2 2 2 2 n n k m U m n k k a   = +   − +      (0) (1) (0) (0) (0) (0) k k k k k k k k k k k H E E           = + = + −  ( ) ( ) 2 2 2 2 0 1 2 exp 2 / 1 2 / ikx n n mU i nx a e L k k n a      = +     − +    2 n k k a  = +