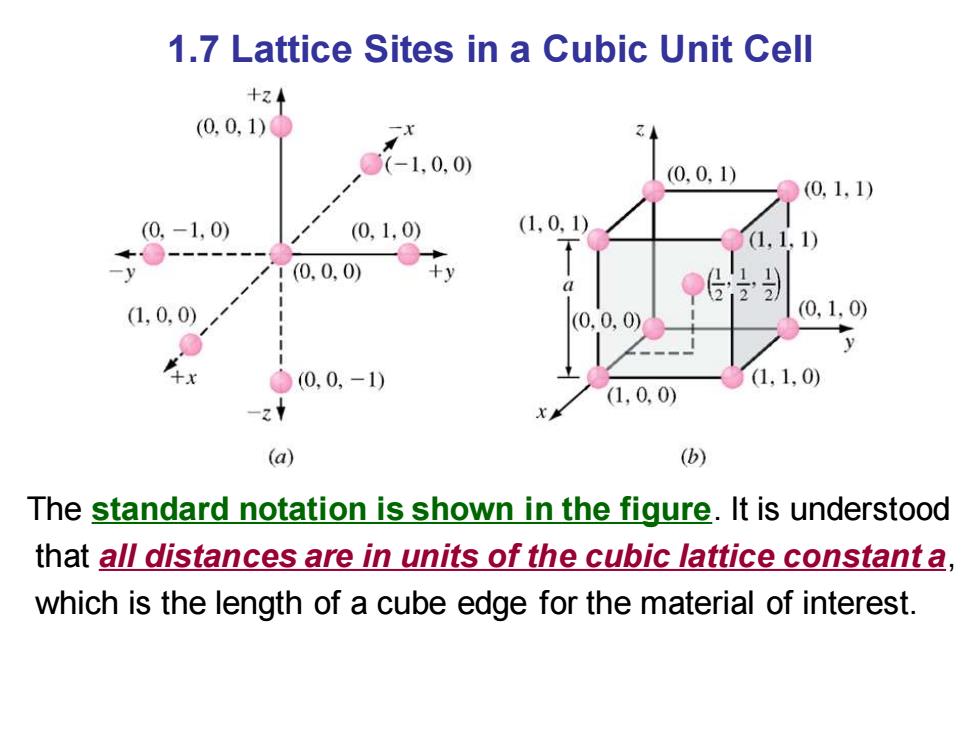
1.7 Lattice Sites in a Cubic Unit Cell +z (0,0,1) (-1,0,0) (0,0,1) (0,1,1) (0,-1,0) (0,1,0) (1,0,1) (1,1, 1) y 1(0.0,0) +y 0 (1,0,0) (0,0,0) (0,1,0) ●0,0,-1) (1,1,0) (1,0,0) (a) (b) The standard notation is shown in the figure.It is understood that all distances are in units of the cubic lattice constant a, which is the length of a cube edge for the material of interest
1.7 Lattice Sites in a Cubic Unit Cell The standard notation is shown in the figure. It is understood that all distances are in units of the cubic lattice constant a, which is the length of a cube edge for the material of interest

Directions in a Crystal:Standard Notation Choose an origin,O.consider the lattice vector joining o to any point in space,say point T in the figure.This vector can be written T=n a+n2a2+n3a3 [111 [111]direction In order to distinguish a Lattice Direction from a Lattice Point,(nin2n3),the 3 integers are enclosed in square brackets [.instead of parentheses (.)which are reserved to indicate a Lattice Point
Directions in a Crystal: Standard Notation • Choose an origin, O. consider the lattice vector joining O to any point in space, say point T in the figure. This vector can be written T = n1a1 + n2a2 + n3a3 [111] direction • In order to distinguish a Lattice Direction from a Lattice Point, (n1n2n3 ), the 3 integers are enclosed in square brackets [ .] instead of parentheses (.), which are reserved to indicate a Lattice Point
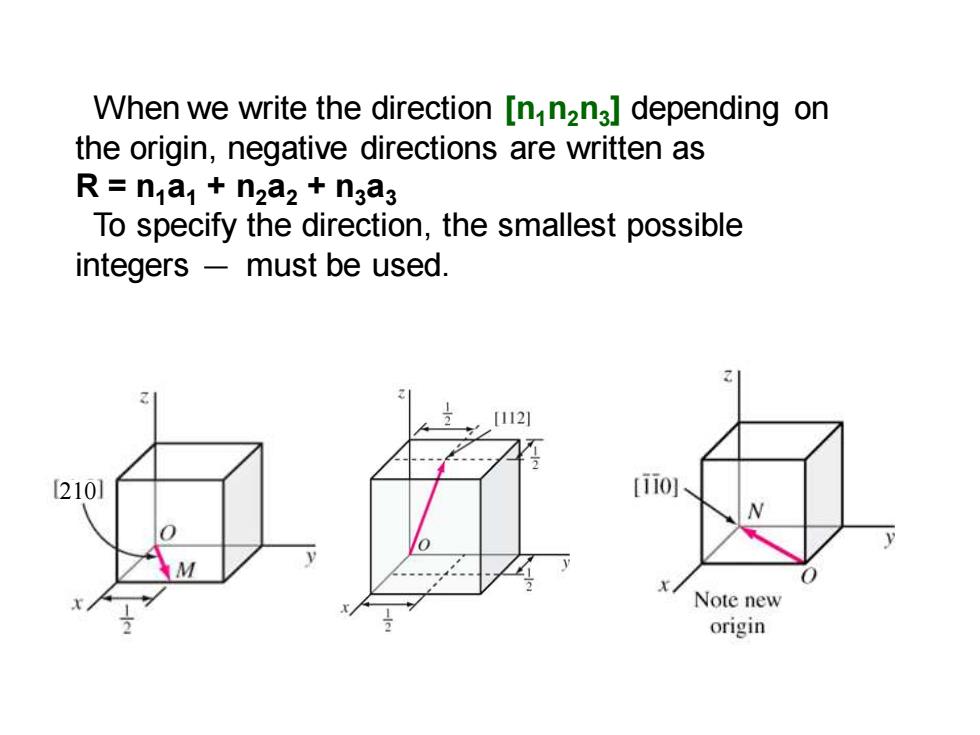
When we write the direction [nn2n3]depending on the origin,negative directions are written as R=n a1+n2a2+n3a3 To specify the direction,the smallest possible integers must be used. [112] [210] [ii01 Note new origin
210 When we write the direction [n1n2n3 ] depending on the origin, negative directions are written as R = n1a1 + n2a2 + n3a3 To specify the direction, the smallest possible integers must be used

1.8 crystal plane and miller index We can view a lattice as a stack of planes,instead of a collection of atoms The Miller index(h,k,I)for crystal planes rules: no need to be primitive vectors 1.取截距(以a1,a2,a3篇單位) 得(,y,z) 2.取倒數(1/x,1y,1/2) 3.通分成互質整數(h,k,) Figure 15 Thie pline interovpts the a ay ates at 3a 2ap 2a The the saue ratin are23.3.and thas the indices of the plane are
1.8 crystal plane and miller index
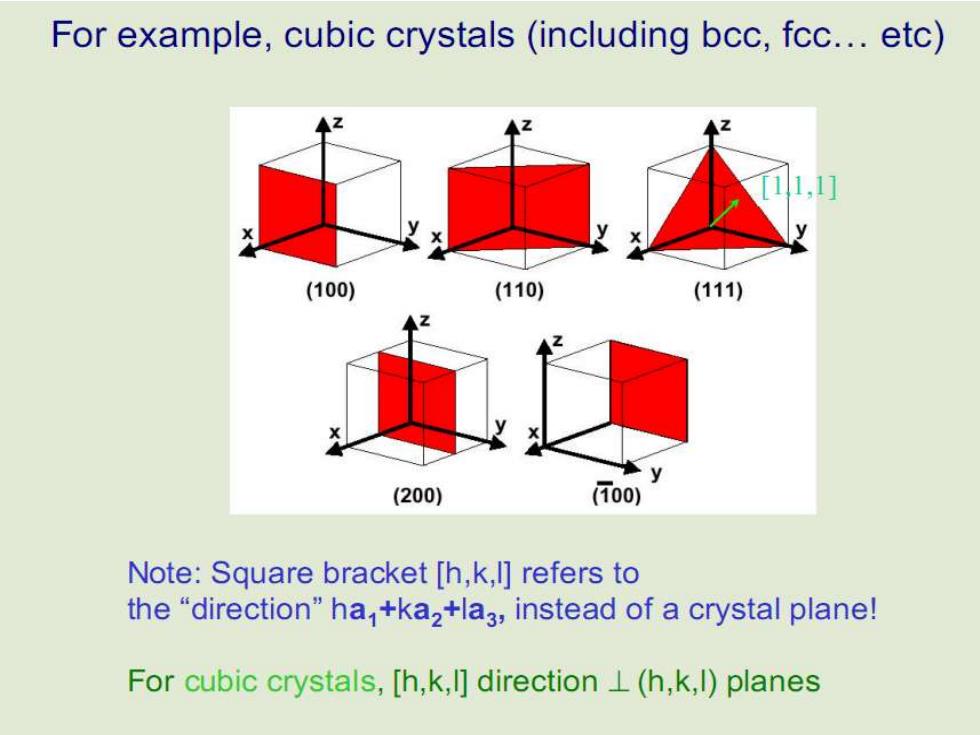
For example,cubic crystals (including bcc,fcc.etc) (100) (110) (111) (200) 00) Note:Square bracket [h,k,I]refers to the"direction"ha,+kaz+la3,instead of a crystal plane! For cubic crystals,[h,k,I]direction L(h,k,l)planes

Miller indices and intercepts a3 ∞a1:∞a2:1a3 ∞a1:1a2:1ag 1a1:∞a2:1a3 001 011 101 1a1:1a2:1a 111 100 010 110 ∞a1:1a2:a3 1a1:∞a2:∞a3 1a1 1a1:1a2:∞a3
Crystal Structure 6

Indices of a Family of Planes Sonetimes.when the unit cell has rotational symmetry, several nonparallel planes may be equivalent by virtue of this symmetry,in which case it is convenient to lump all these planes in the same Miller Indices,but with curly brackets. {100}=(100),(010),(001),(010),(001),(100) {111}≡(111),111),(111),(111),(111),(111),(11),(11I) Thus indices (h,k,1}represent all the planes equivalent to the plane (hkl)through rotational symmetry
7 • Sometimes. when the unit cell has rotational symmetry, several nonparallel planes may be equivalent by virtue of this symmetry, in which case it is convenient to lump all these planes in the same Miller Indices, but with curly brackets. Thus indices {h,k,l} represent all the planes equivalent to the plane (hkl) through rotational symmetry. {111} (111),(111),(111),(111),(1 1 1),(1 11),(111),(11 1) {100} (100),(010),(001),(010),(001),(100) Indices of a Family of Planes

Actual Si(001)surface under STM(Kariotis and Lagally,1991) Surface reconstruction(表面重構) Fig.4.16.Structural model for the Si(001)2x1 surface