《固体物理学》课程教学课件（PPT讲稿）Chapter 4 lattice dynamics and lattice capacity 4.5 Heat capacity of the lattice

4.5 Heat capacity of the lattice 6E Cy Dugong-Petit law,numerical value aT =3R independent of T Classical Statistical no numerical value at finite T Mechanics >k. For a vibrating atom: E=K+U .N =m+号mv2+m+号k,x2+k,y2+号k.z2 Classical statistical mechanics-equipartition theorem:in thermal equilibrium each quadratic term in the E has an average energy 5kg7,s0:E,=6kT)=3k7 Classically for a vibrator Cy

4.5 Heat capacity of the lattice Classical Statistical Mechanics Dugong-Petit law, numerical value independent of T no numerical value at finite T Classically for a vibrator 2 2 2 1 2 2 1 2 2 1 2 2 1 2 2 1 2 1 1 mv mv mv k x k y k z E K U = x + y + z + x + y + z m = + ky kx kz For a vibrating atom: Classical statistical mechanics — equipartition theorem: in thermal equilibrium each quadratic term in the E has an average energy , so: k T 2 B 1 E 6( kB T) 3kB T 2 1 1 = =

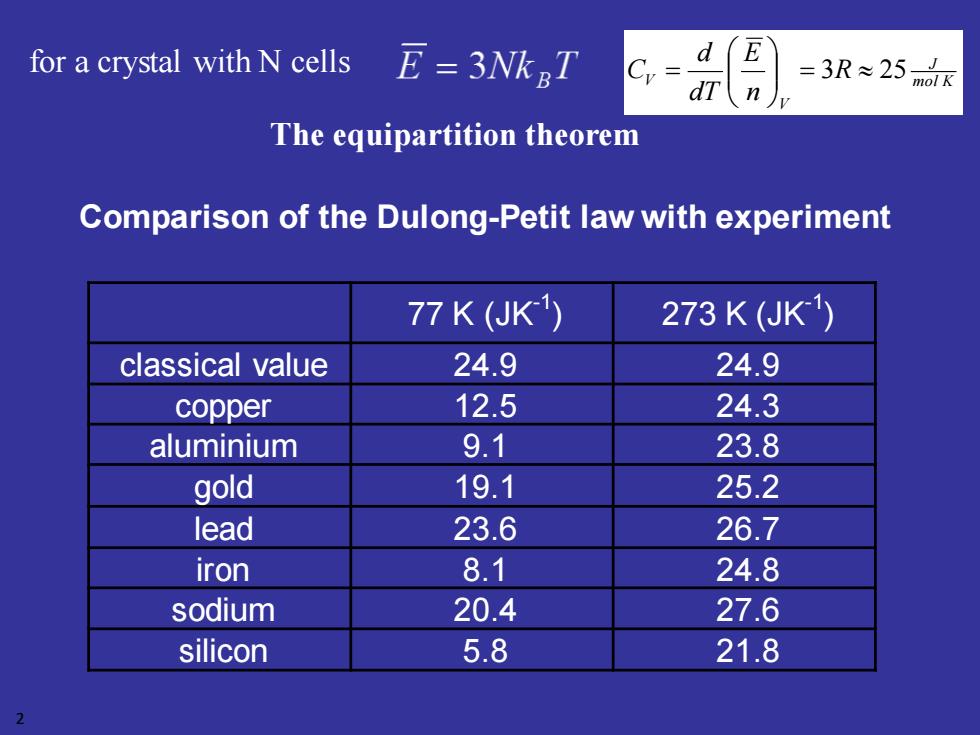
for a crystal with N cells E=3NkT d E =3R≈25 dT mol K n The equipartition theorem Comparison of the Dulong-Petit law with experiment 77K(UK1) 273K(JK1) classical value 24.9 24.9 copper 12.5 24.3 aluminium 9.1 23.8 gold 19.1 25.2 lead 23.6 26.7 iron 8.1 24.8 sodium 20.4 27.6 silicon 5.8 21.8 2

Comparison of the Dulong-Petit law with experiment 77 K (JK-1 ) 273 K (JK-1 ) classical value 24.9 24.9 copper 12.5 24.3 aluminium 9.1 23.8 gold 19.1 25.2 lead 23.6 26.7 iron 8.1 24.8 sodium 20.4 27.6 silicon 5.8 21.8 2 for a crystal with N cells The equipartition theorem mol K J V V R n E dT d C = 3  25         =

The vibration mode with frequency of is composed of subsystems 1 E,=(n,+ho, ThepmhabitoisuoyseanthegentmsaeorE-ah -n ho/kgT e P n ho/kgT P=e-eo)∑=-x Theavcrmgeprohabilit T'heaverngeenenyTor thivihrntionmoie E=∑PE ho e (eho,kar-1) the relation between lattice vibration frequency and temperature

The vibration mode with frequency of j is composed of subsystems The probability of subsystem in the quantum state of The average probability The average energy for this vibration mode / 1 ( ) 2 1 j B j E Tj j k T e   = +  − the relation between lattice vibration frequency and temperature / 2 / 2 ( ) ( 1) j B j B k T j V B k T B e C k k T e    = −

oj/kgT C,=k, e o,k-1） (e kgT >>ho ha, =1+ hightemperature ho Cy= Cr≈kB Dugong-Petit law 00088 kgT1 T→0 Cv→0 consistent with the experimental results

/ 2 / 2 ( ) ( 1) j B j B k T j V B k T B e C k k T e    = − 2 2 2 (1 ) ( ) 1 [ ( ) ] 2 j j B V B B j j B B k T C k k T k T k T     + + = + high temperature Dugong-Petit law 2 / 1 ( ) j B j V B k T B C k k T e   = —— consistent with the experimental results low temperature

4.5.1 Einstein model ho e isuWehecrlcopeselofNatomsvibrnteswiththesnme freuenyog 3N E= ho Nha+ 3Nh@ Total energy )=2 ehab/kgT eha/kgT capacity Cy=( (e C,=3Nk/.K hoo/kgT e -Einstein heat e capacity function

3 ( ) 0 k T C Nk f B V B B  = 4.5.1 Einstein model Assume the crystal composed of N atoms vibrates with the same frequency 0 / 1 ( ) 2 1 j B j E Tj j k T e   = +  − capacity Total energy / 2 / 0 0 2 ( 1) ( ) ( ) 0 0 − = k T k T B B B B B e e k T k T f         -Einstein heat capacity function

Einstein temperature h@o k2Og hoo eir g 0:=ka G,=3x,号 for the majority of solids (ee-12 0。=100K~300K 6×4.18 5×4.18 24×4.18 是3×418 G2×4.18 1×4.18 00.10.20.30.40.50.60.70.80.91.0 XCH003013 T/O Diamond 0E=1320K

Einstein temperature B E k 0   = / 2 / 2 ( 1) 3 ( ) − = T T E V B E E e e T C Nk    for the majority of solids Diamond

hightcmperature ho1k9e=h0, 0>T kgT er1C=3,2 xperimental Cy=AT3

CV  3NkB B E 0 k   = high temperature consistent with the experimental results low temperature k T B V B B e k T C Nk 0 0 2 3 ( )     − = B E 0 k   = Experimental

Despite its success in reproducing the approach of Cy->0 as T >0,the Einstein model is clearly deficient at very low T.What might be wrong with the assumptions it makes? 3N independent oscillators,all with frequency o Discrete allowed energies: En=nhon=0,l,2,. ● At high T the small spacing between the energy levels is irrelevant. At sufficiently low temperature,the energy level separation is much bigger than kBT. Eventually all the oscillators are "frozen"in the ground state.Increasing T a little does not change this,i.e.it does not change the energy

• At high T the small spacing between the energy levels is irrelevant. • At sufficiently low temperature, the energy level separation is much bigger than kBT. • Eventually all the oscillators are “frozen” in the ground state. Increasing T a little does not change this, i.e. it does not change the energy. Despite its success in reproducing the approach of CV → 0 as T → 0, the Einstein model is clearly deficient at very low T. What might be wrong with the assumptions it makes? • 3N independent oscillators, all with frequency  • Discrete allowed energies: E = n n = 0,1, 2, . n 

Debye developed a more sophisticated treatment of atomic vibrations in solids Debye's model of a solid: 3N normal modes (patterns)of oscillations 。 Spectrum of frequencies from=0tomax Treat solid as continuous elastic medium (ignore details of atomic structure) 1)3 independent polarizations(L,T1,T2)with equal propagation speeds 2)continuous,elastic solid:=vk 3)x given by the value that gives the correct number of modes per polarization (N) This changes the expression for Cy because each mode of oscillation contributes a frequency-dependent heat capacity and we now have to integrate over all o:

Debye developed a more sophisticated treatment of atomic vibrations in solids. Debye’s model of a solid: • 3N normal modes (patterns) of oscillations • Spectrum of frequencies from  = 0 to max • Treat solid as continuous elastic medium (ignore details of atomic structure) This changes the expression for CV because each mode of oscillation contributes a frequency-dependent heat capacity and we now have to integrate over all : 1) 3 independent polarizations (L, T1 , T2 ) with equal propagation speeds 2) continuous, elastic solid:  = vgk 3) max given by the value that gives the correct number of modes per polarization (N)

4.5.2 Debye model 1912,Debye propose a model of continuous elastic media wave for the vibration waves @=Cq For Lognitudinal Wave Dispersion relation @=Cq For Transverse Wave For 3d crystal,the DoS (2n) V:the volume XCH003014 qy dq da da,dq the values of g are separated and distributed uniformly dq da,dq,dq. 9→q+dg (2π) The number of states (2π)月 4网dg

4.5.2 Debye model 1912, Debye propose a model of continuous elastic media wave for the vibration waves l t C q For Lognitudinal Wave C q For TransverseWave   = = Dispersion relation For 3d crystal , the DoS V: the volume q dq V 2 3 4 (2 )   The number of states the values of q are separated ， and distributed uniformly