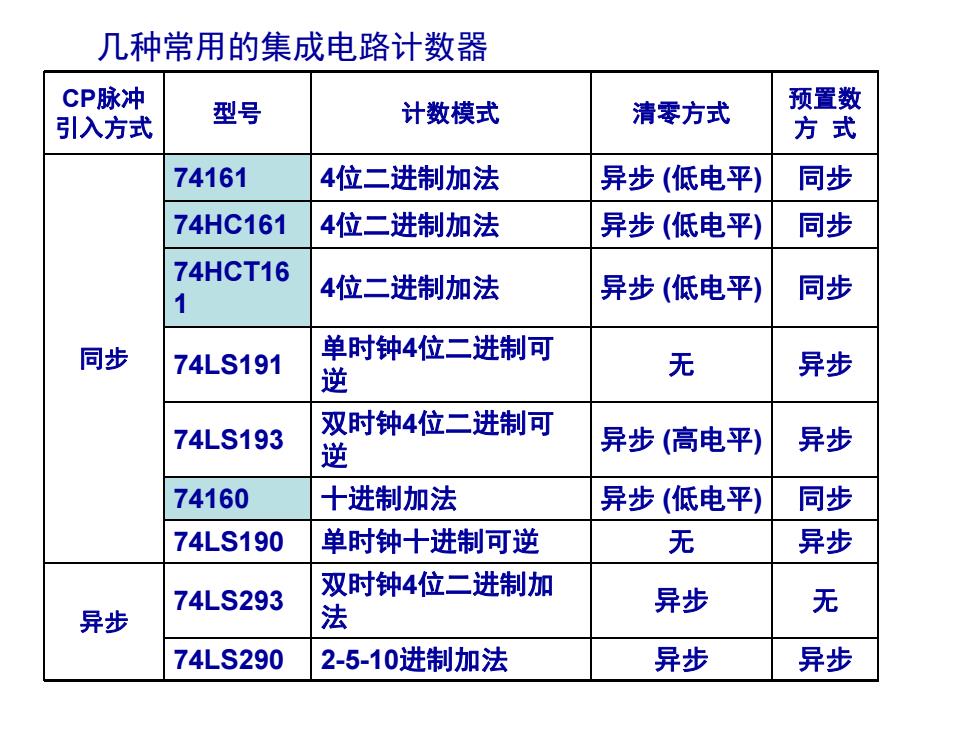
几种常用的集成电路计数器 CP脉冲 引入方式 型号 计数模式 清零方式 预置数 方式 74161 4位二进制加法 异步(低电平) 同步 74HC161 4位二进制加法 异步(低电平) 同步 74HCT16 4位二进制加法 异步(低电平) 同步 同步 74LS191 单时钟4位二进制可 逆 无 异步 74LS193 双时钟4位二进制可 逆 异步(高电平) 异步 74160 十进制加法 异步(低电平) 同步 74LS190 单时钟十进制可逆 无 异步 74LS293 双时钟4位二进制加 异步 无 异步 法 74LS290 2-5-10进制加法 异步 异步
CP脉冲 引入方式 型号 计数模式 清零方式 预置数 方 式 同步 74161 4位二进制加法 异步 (低电平) 同步 74HC161 4位二进制加法 异步 (低电平) 同步 74HCT16 1 4位二进制加法 异步 (低电平) 同步 74LS191 单时钟4位二进制可 逆 无 异步 74LS193 双时钟4位二进制可 逆 异步 (高电平) 异步 74160 十进制加法 异步 (低电平) 同步 74LS190 单时钟十进制可逆 无 异步 异步 74LS293 双时钟4位二进制加 法 异步 无 74LS290 2-5-10进制加法 异步 异步 几种常用的集成电路计数器
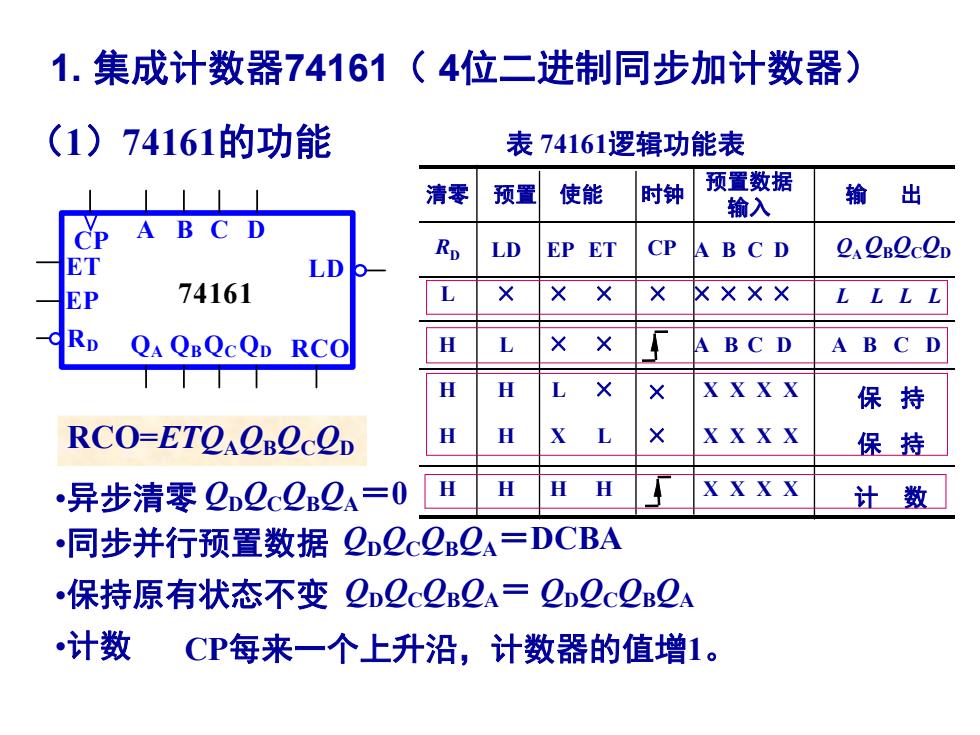
1.集成计数器74161(4位二进制同步加计数器) (1)74161的功能 表74161逻辑功能表 清零 预置 使能 时钟 预置数据 输入 输 出 CP A BC D Rp LD EP ET CP A BCD 2.OB2cOD ET LD EP 74161 × L RD QA QBQcQD RCO H L X A AB C D H H X XXXX 保持 RCO-ETOAOBOCOD H H XXXX 保持 •异步清零2D2c2B2A=0 H H HH XXXX 计数 ·同步并行预置数据QDQc2B2A=DCBA ·保持原有状态不变2D2c2B2A=2D2c2B2A 计数 CP每来一个上升沿,计数器的值增1
1. 集成计数器74161( 4位二进制同步加计数器) (1)74161的功能 CP A B C D ET EP QA QBQCQD RCO 74161 > LD RD RCO=ETQAQBQCQD 表 74161逻辑功能表 × 保 持 H L × × A B C D A B C D L × × × × × × × × RD LD EP ET CP A B C D QA QBQCQD 输 出 预置数据 输入 预置 使能 时钟 L L L L H H L × X X X X H H X L × X X X X 保 持 H H H H X X X X 计 数 清零 •异步清零 •同步并行预置数据 •保持原有状态不变 •计数 QDQCQBQA=0 QDQCQBQA=DCBA QDQCQBQA= QDQCQBQA CP每来一个上升沿,计数器的值增1
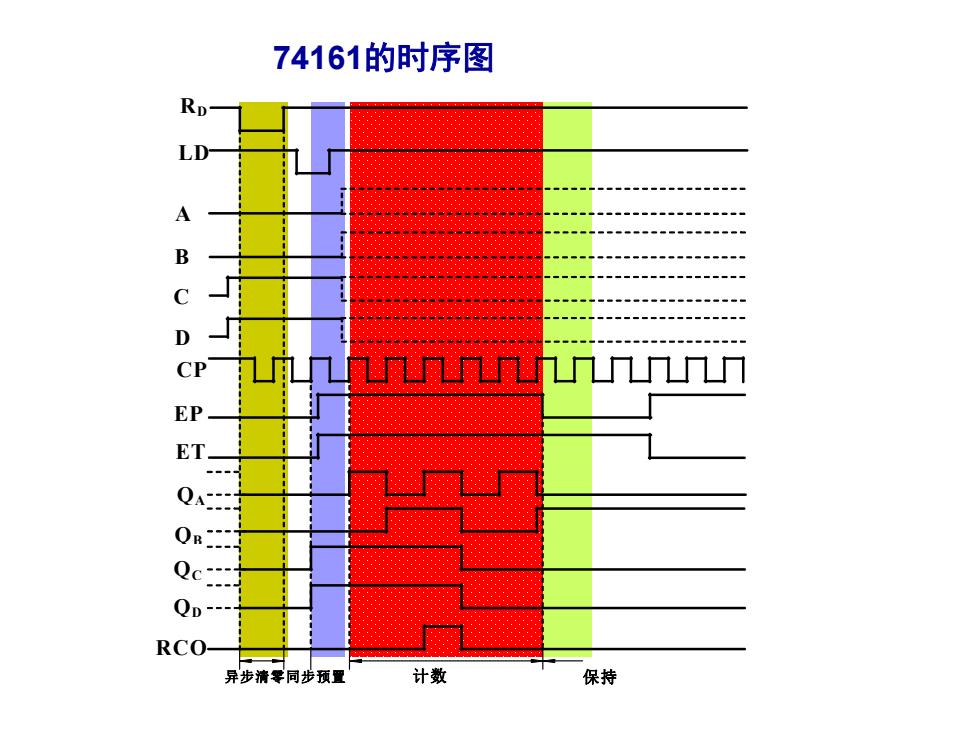
74161的时序图 RD B EP E 0 Qp RCO 异步清零同步预置 计数 保持
74161的时序图 RD LD A B C D CP EP ET QA QB QC QD RCO 异步清零同步预置 计数 保持

用集成计数器构成任意进制计数器的方法 N<M的情况:已有的集成计数器是M进制,需组成的 是N进制计数器 具体实现的方法: 反馈清零法 利用清零输入端,使电路计数到某状态 时产生清零操作,清除M-N个状态实现 N进制计数器。 反馈置数法 利用计数器的置数功能,通过给计数器 重复置入某个数码的方法减少M-N)个 独立状态,实现W进制计数器的
用集成计数器构成任意进制计数器的方法 •N < M 的情况 :已有的集成计数器是M 进制,需组成的 是N 进制计数器 具体实现的方法: 反馈清零法 反馈置数法 利用清零输入端,使电路计数到某状态 时产生清零操作,清除M–N个状态实现 N进制计数器。 利用计数器的置数功能,通过给计数器 重复置入某个数码的方法减少(M–N)个 独立状态,实现N进制计数器的

N>M的情况 -采用多片M进制计数器构成。 按芯片连接方式可分为: (1)串行进位方式:构成异步计数器 (2)并行进位方式:构成同步计数器
•N >M 的情况 (1)串行进位方式: (2)并行进位方式: ----采用多片M进制计数器构成。 按芯片连接方式可分为: 构成异步计数器 构成同步计数器
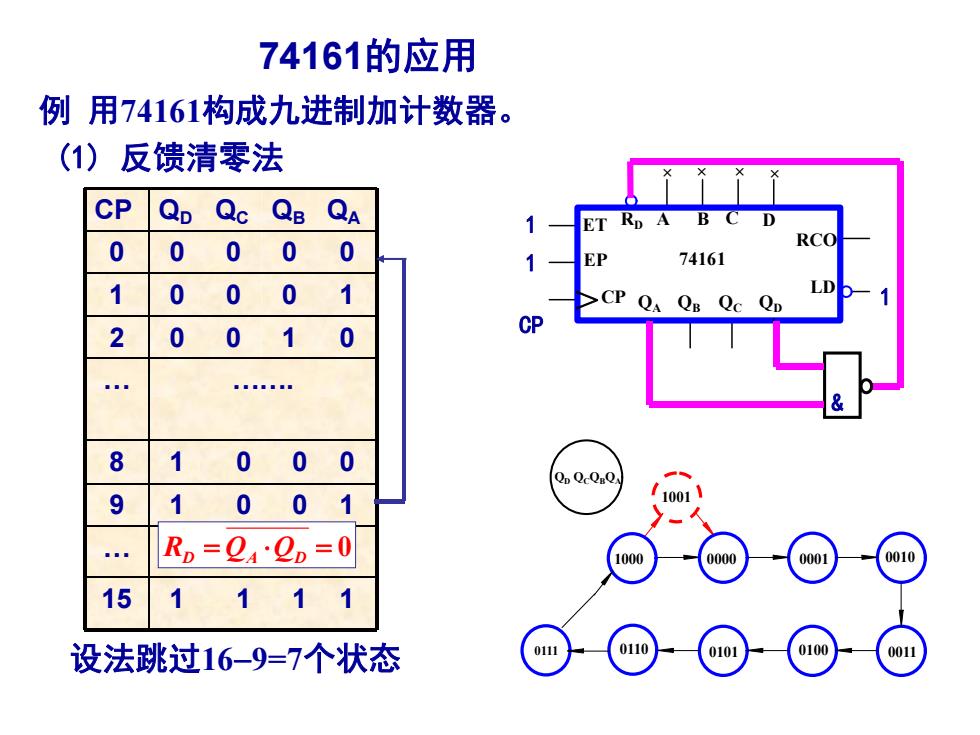
74161的应用 例用74161构成九进制加计数器。 (1)反馈清零法 CP QD Qc QB QA ET RD A B C D 0 RCO 0 0 0 EP 74161 1 0 00 CP QA QB Qc QD 2 0 0 1 0 Cp BA 0a■■ 8 1 0 0 0 Qp QCQBQ 9 1 0 0 1 10011 … Rp=04Op=0 1000 0000 0001 0010 15 1 1 设法跳过16-9=7个状态 0111 0110 0101 0100
设法跳过169=7个状态 1 1 CP 1 > 74161 QA QB QC QD LD RCO ET RD A B C D EP CP × × × × 1 1 CP & 1 0111 0000 0001 0010 0110 0101 0100 0011 1000 1001 QD QCQBQA 1000 例 用74161构成九进制加计数器。 74161的应用 CP QD QC QB QA 0 0 0 0 0 1 0 0 0 1 2 0 0 1 0 … ……. 8 1 0 0 0 9 1 0 0 1 … …… 15 1 1 1 1 0 RD QA QD ((11)) 利反用馈异清步零清法零引脚

例用74161构成九进制加计数器。 (2)反馈置数法: CP Qp Qc QB QA 0 0 0 00 ETRp A B C D 1 0 0 0 1 EP 74161 D 2 0 CP- 0 1 0 CP QA QB Qc QD 是A.a 8 0 0 0 9 0 0 1 Qp Qc Q8 Q LD=OD 1000 0000 0001 0010 … 15 1 1 1 0111 0110 0101 0100 0011 设法跳过16-9=7个状态
> RCO ET EP 1 1 CP 1 RD A B C D CP QA QB QC QD 1 74161 LD 1000 0000 0001 0010 0111 0110 0101 0100 0011 QD QC QB QA 设法跳过169=7个状态 CP QD QC QB QA 0 0 0 0 0 1 0 0 0 1 2 0 0 1 0 … ……. 8 1 0 0 0 9 1 0 0 1 … …… 15 1 1 1 1 例 用74161构成九进制加计数器。 LD QD (2) 利反用馈同置步数置法数: 引脚: 采用前九种状态