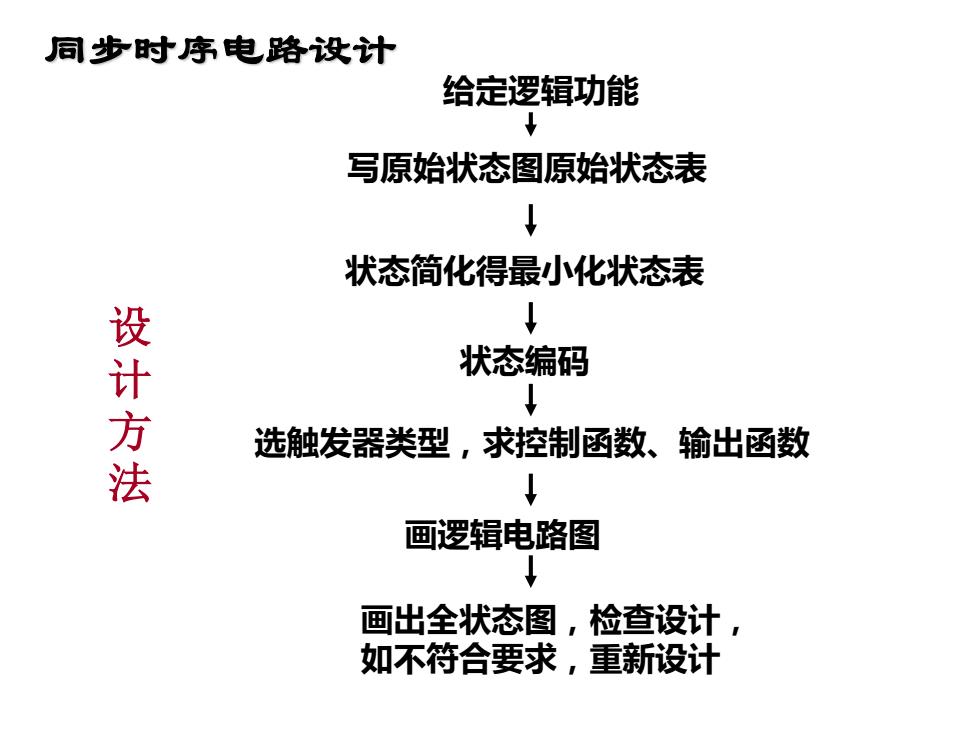
同步时序电路设计 给定逻辑功能 写原始状态图原始状态表 ↓ 状态简化得最小化状态表 ↓ 设计方法 状态编码 ↓ 选触发器类型,求控制函数、输出函数 ↓ 画逻辑电路图 ↓ 画出全状态图,检查设计, 如不符合要求,重新设计
同步时序电路设计 设 计 方 法 给定逻辑功能 写原始状态图原始状态表 状态简化得最小化状态表 状态编码 选触发器类型,求控制函数、输出函数 画逻辑电路图 画出全状态图,检查设计, 如不符合要求,重新设计
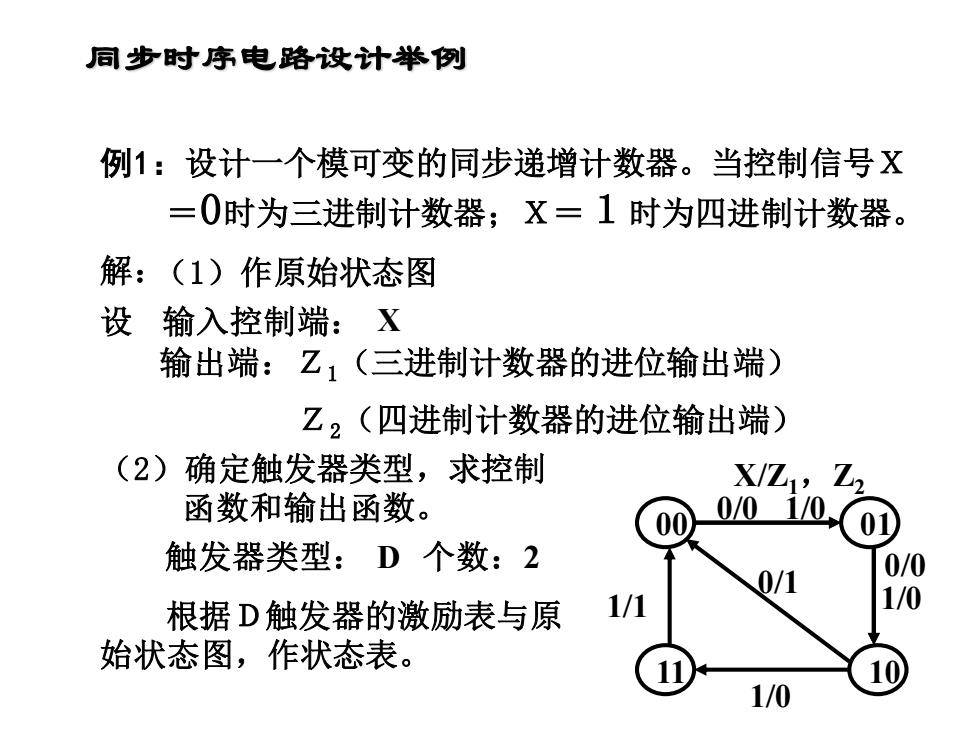
同步时序电路设计举例 例1:设计一个模可变的同步递增计数器。当控制信号X =0时为三进制计数器;X=1时为四进制计数器。 解:(1)作原始状态图 设输入控制端 :X 输出端:Z1(三进制计数器的进位输出端) Z2(四进制计数器的进位输出端) (2)确定触发器类型,求控制 X/Z1, 函数和输出函数。 00 0/0 1/0 01 触发器类型:D个数:2 0/1 0/0 根据D触发器的激励表与原 1/1 1/0 始状态图,作状态表。 1/0
同步时序电路设计举例 例1:设计一个模可变的同步递增计数器。当控制信号X =0时为三进制计数器;X=1时为四进制计数器。 解:(1)作原始状态图 设 输入控制端: 输出端:Z1(三进制计数器的进位输出端) Z2(四进制计数器的进位输出端) 00 01 11 10 X/Z1,Z2 0/0 0/0 0/1 1/0 1/1 (2)确定触发器类型,求控制 函数和输出函数。 触发器类型: D 个数:2 根据D触发器的激励表与原 始状态图,作状态表。 1/0 1/0 X
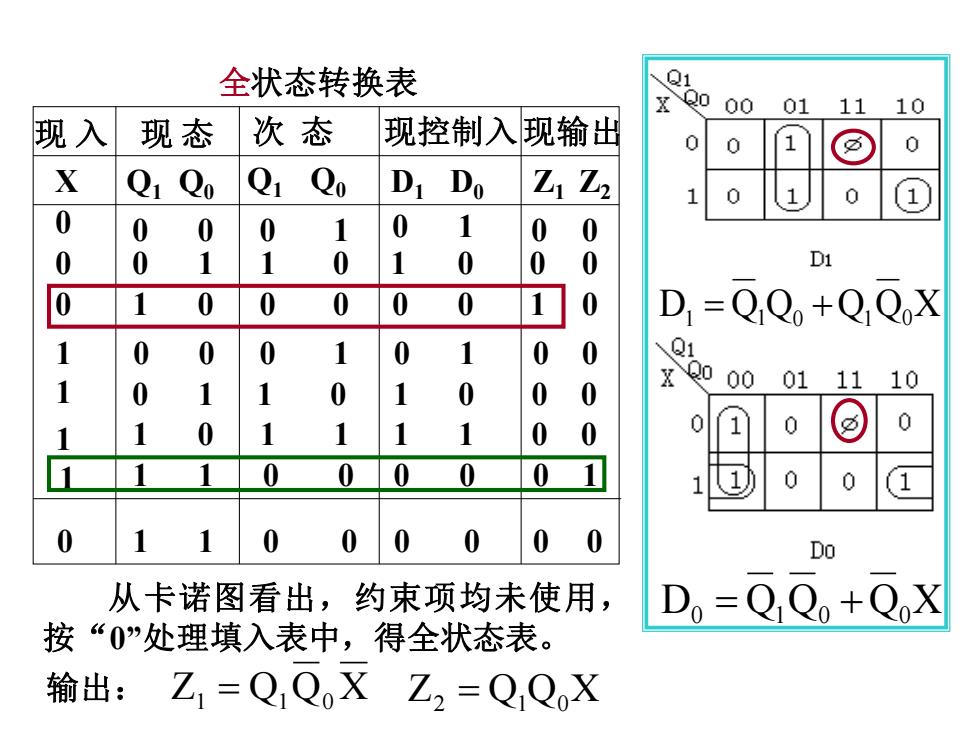
全状态转换表 Q1 xQ如 00 01 11 10 现入 现态 次态 现控制入现输出 0 X Q1 Qo Qo D Do ZZ 0 0 0 0 0 1 0 1 0 0 0 0 1 0 0 Di 0 1 0 0 0 0 0 1 D =QQo+QQ0X 1 0 0 0 0 Q1 Q如00 01 0 0 0 11 10 1 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 Do 从卡诺图看出,约束项均未使用, Do=QjQo+QoX 按“0”处理填入表中,得全状态表。 输出: Z=QQoX Z2=QQoX
1 1 0 现 入 X 现 态 Q1 Q0 现控制入 D1 D0 次 态 Q1 Q0 0 0 0 0 0 0 1 1 0 1 1 1 1 0 0 0 1 0 1 1 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 现输出 Z1 Z2 0 0 0 0 0 1 D1 = Q1 Q0 +Q1 Q0 X 从卡诺图看出,约束项均未使用, D0 = Q1 Q0 +Q0 X 按“0”处理填入表中,得全状态表。 0 1 1 0 0 0 0 0 0 输出: Z1 = Q1 Q0 X Z2 = Q1 Q0 X 全状态转换表 0 0 1 0 1 1 0 0 0 1 0 1 0 1 1 0 1 1 0
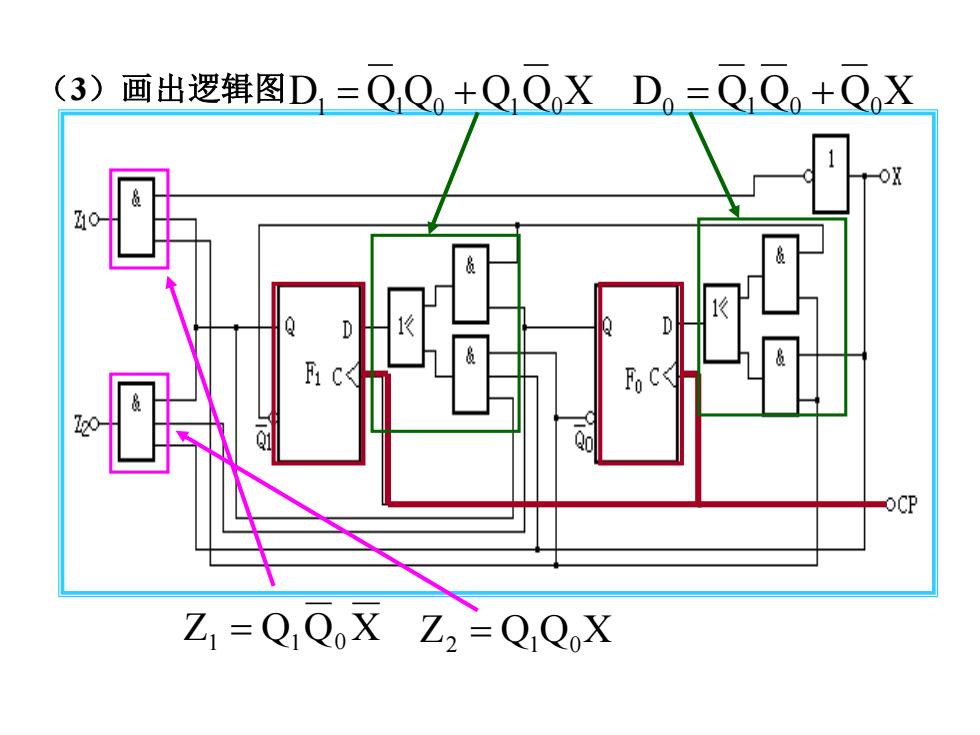
(3) 画出逻辑图D,=QQ+Q,QXD。=Q,Q+QX 10 OCP Z =Q QoX Z2 =QQoX
(3)画出逻辑图 D1 = Q1 Q0 +Q1 Q0 X D0 = Q1 Q0 +Q0 X Z1 = Q1 Q0 X Z2 = Q1 Q0 X
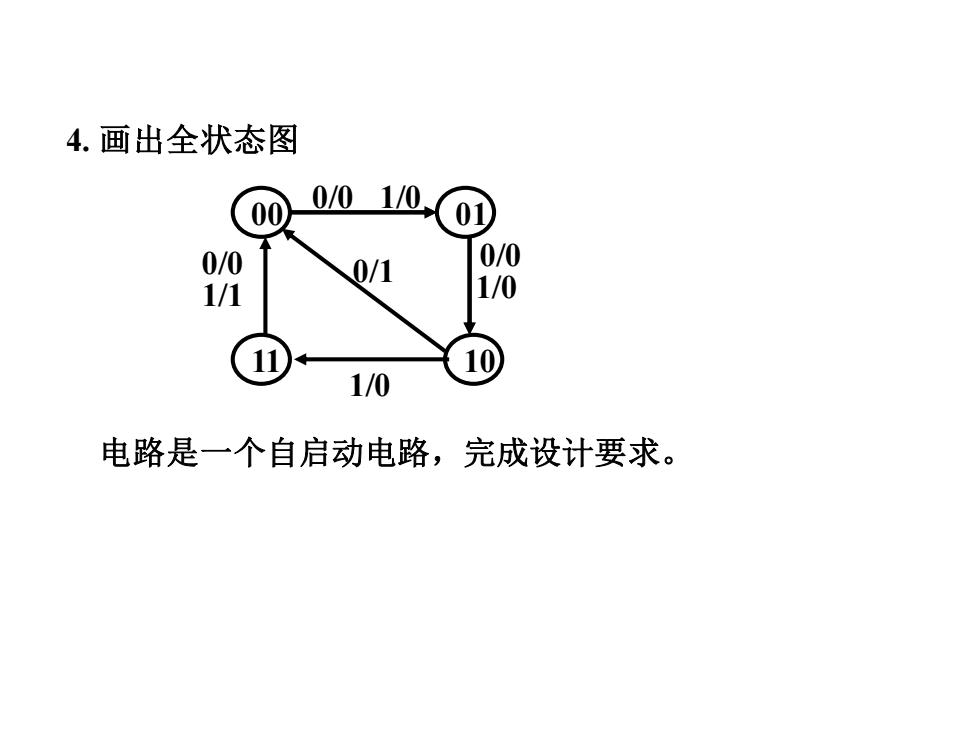
4.画出全状态图 0/01/0 01 0/0 0/1 0/0 1/1 1/0 1/0 电路是一个自启动电路,完成设计要求
4. 画出全状态图 00 01 11 10 0/0 0/0 0/1 1/1 1/0 1/0 1/0 0/0 电路是一个自启动电路,完成设计要求

例2 试设计一个四进制加法计数器。 解: 1.根据设计要求,确定输入、输出及电路的状态, 进而拟定原始状态表和原始状态图。 根据题意可知电路应有四个同的状态,分别用 S0、S1、S2、S来表示该四种不同的状态。在状态 为S时输出子1。当输入第四个计数脉冲时,计数器 返回初始状态S,同时输出☑向高位计数器送出一个进 位脉冲。其原始状态表、状态图如下所示
例2 试设计一个四进制加法计数器。 解: 1.根据设计要求,确定输入、输出及电路的状态, 进而拟定原始状态表和原始状态图。 根据题意可知电路应有四个同的状态,分别用 S0、S1、S2、S3来表示该四种不同的状态。在状态 为S3时输出Z=1。当输入第四个计数脉冲时,计数器 返回初始状态S0,同时输出Z向高位计数器送出一个进 位脉冲。其原始状态表、状态图如下所示
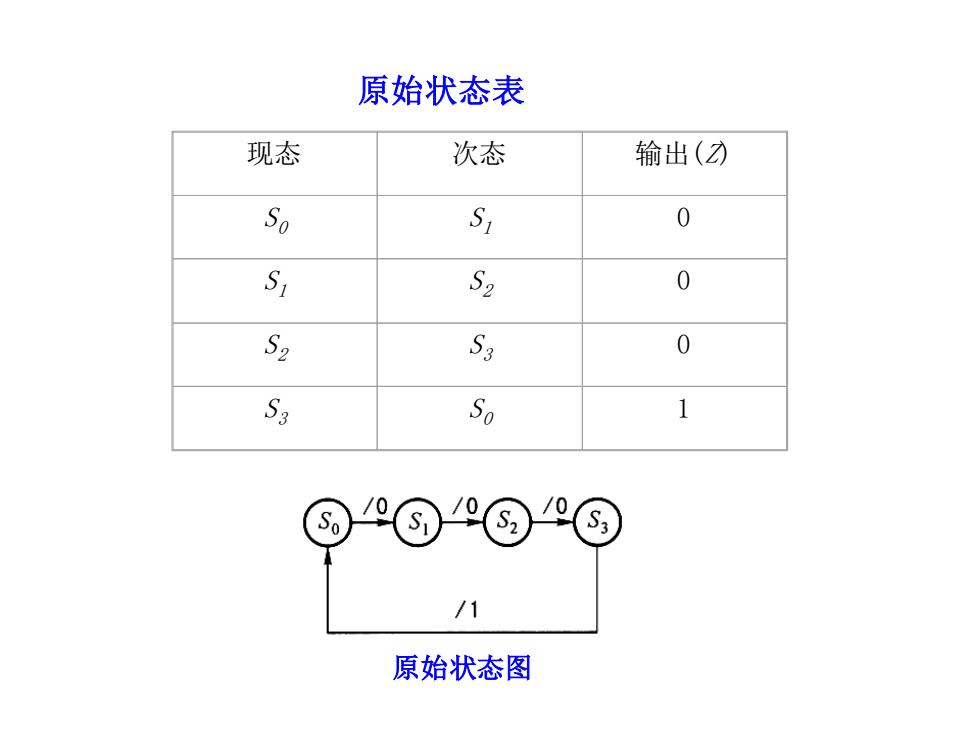
原始状态表 现态 次态 输出() So S1 0 S1 S2 0 S2 Sa Sa So / 原始状态图
原始状态表 现态 次态 输出(Z) S0 S1 0 S1 S2 0 S2 S3 0 S3 S0 1 原始状态图

2.化简原始状态表,消去多余的状态,求得最小 化状态表。 从原始状态表可以看出无多余状态,已不能再 作状态化简。 3.对简化后的状态表进行状态编码即进行状态赋 值,把状态表中用文字标注的每个状态用二进 制代码表示。这一步得到一个二进制状态表。 由N≤2n可知,在N=4时,n=2,即采用两位二进 制代码。设S,00、S01、S,10、S11。则可 得状态编码表,如下表所列
2.化简原始状态表,消去多余的状态,求得最小 化状态表。 从原始状态表可以看出无多余状态,已不能再 作状态化简。 3.对简化后的状态表进行状态编码即进行状态赋 值,把状态表中用文字标注的每个状态用二进 制代码表示。这一步得到一个二进制状态表。 由N≤2 n可知,在N=4时,n=2,即采用两位二进 制代码。设S0 =00、S1 =01、S2 =10、S3 =11。则可 得状态编码表,如下表所列
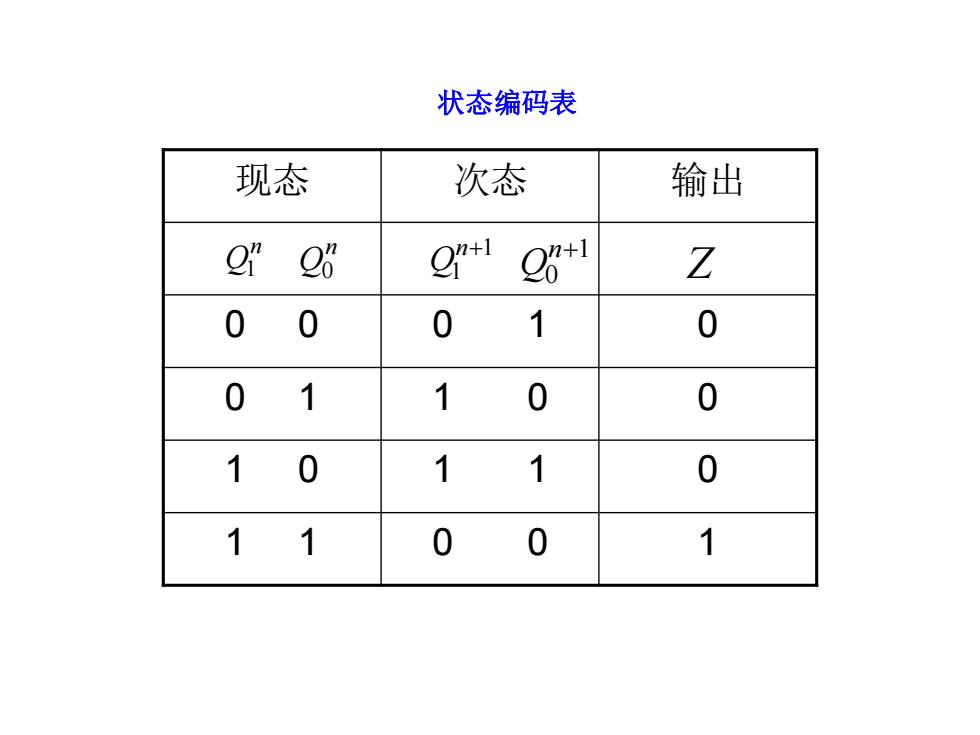
状态编码表 现态 次态 输出 0"2 Q1Q+ Z 0 0 0 1 0 0 1 1 0 0 1 0 1 1 0 11 0 0 1
状态编码表 现态 次态 输出 0 0 0 1 0 0 1 1 0 0 1 0 1 1 0 1 1 0 0 1 n Q1 n Q0 1 1 n+ Q 1 0 n+ Q Z

4.选定触发器的类型,并求出激励函数和输出 函数表达式。 我们选用了-触发器,根据状态编码表可得: Q+1=9"Q+Q"Q Q+1=Q"Q6+Q"Q=Q6 Z 0"o 因为J-K触发器的特性方程为Q+1=JQ”+KQ 则可得: J1=K1=Q6 J0=K0=1
4.选定触发器的类型,并求出激励函数和输出 函数表达式。 我们选用J-K触发器,根据状态编码表可得: n n n n n Q Q1 Q0 Q1 Q0 1 1 = + + n n n n n n Q Q1 Q0 Q1 Q0 Q0 1 0 = + = + n n Z = Q1 Q0 因为J-K触发器的特性方程为 n n n Q = JQ + KQ +1 则可得: n J1 = K1 = Q0 1 J0 = K0 =