
考虑特殊问题的逻辑设计 1多输出函数的逻辑设计 2利用任意项的逻辑设计 3考虑级数的逻辑设计
考虑特殊问题的逻辑设计 1 多输出函数的逻辑设计 2 利用任意项的逻辑设计 3 考虑级数的逻辑设计

1 多输出函数的逻辑设计 设计多输出电路的特殊问题是: 确定各输出函数的公用项,以 组合逻辑电路 使整个电路为最简,而不片面追求 每个输出函数为最简。 AA2 「例10]用与非门实现下列多输出函数: F=Σ(1,3,4,5,7) F2=∑(3,4,7) 解:化简上述函数,可得
1 多输出函数的逻辑设计 A1A2 An F1 F2 Fn 组合逻辑电路 设计多输出电路的特殊问题是: 确定各输出函数的公用项,以 使整个电路为最简,而不片面追求 每个输出函数为最简。 [例10] 用与非门 实现下列多输出函数: F1=∑(1,3,4,5,7) F2= ∑(3,4,7) 解:化简上述函数,可得

F=C+AB=CAB 如果从全局出发统一考虑F和F2 的各组成项,可将左式更改为: (F,=BC+ABC=BCAB元 F=C+ABC 按此化简结果,可画出如图(a) F2=BC+ABC 所示的逻辑图。 则画出如图(b)所示的逻辑图。 F2 AB ABC BC ABC BC (a) (b)
按此化简结果,可画出如图(a) 所示的逻辑图。 (a) F1 F2 C A B ABC B C (b) F1 F2 C ABC B C F1= C + AB = C AB F2= BC + ABC = BC ABC F1= C + ABC F2= BC + ABC 则画出如图(b)所示的逻辑图。 如果从全局出发统一考虑F1和 F2 的各组成项,可将左式更改为:

2利用任意项的逻辑设计 任意项 是指从约束方程推得的逻辑值为0的最顶 也称无关顶。这样,可“任意”地在逻辑表达式中 加入此最小项,使其逻辑表达式为更简单。 [例11]用与非门设计一个判别电路,以判别8421BCD码所 表示的十进制数之值是否大于等于5。 解:由题意知其约束方程为: ∑(10,11,12,13,14,15)=0 然后列真值表如下:
2 利用任意项的逻辑设计 任意项 是指从约束方程推得的逻辑值为 0 的最小项, 也称无关项。 这样,可“任意”地在逻辑表达式中 加入此最小项,使其逻辑表达式为更简单。 [例11] 用与非门设计一个判别电路,以判别8421 BCD码所 表示的十进制数之值是否大于等于 5。 解:由题意知其约束方程为: ∑(10,11,12,13,14,15) = 0 然后列真值表如下:
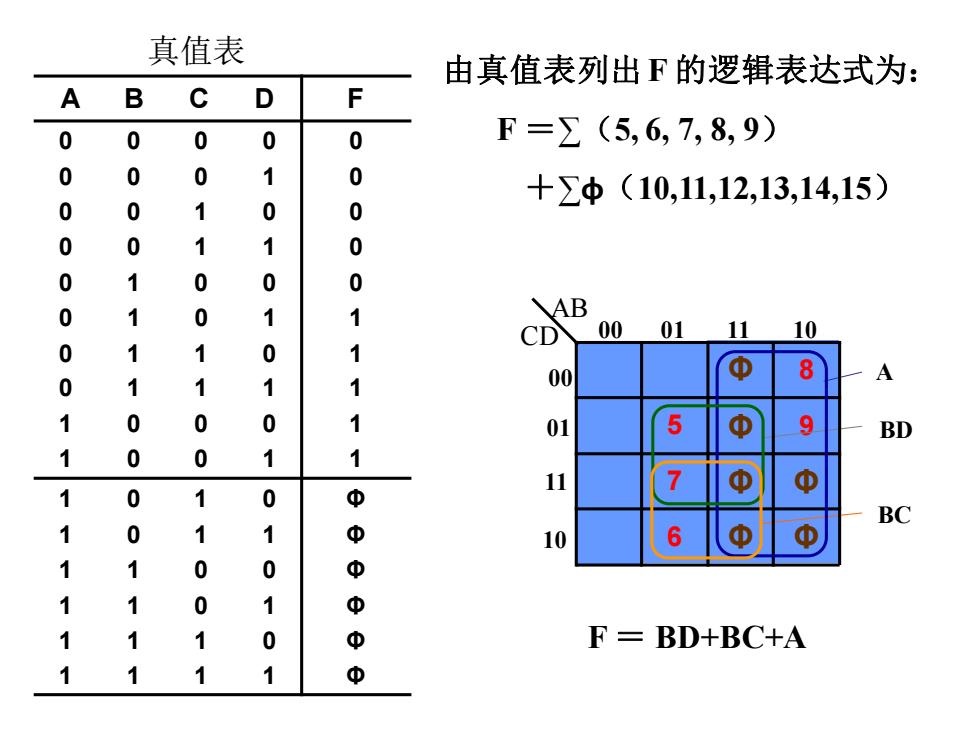
真值表 由真值表列出F的逻辑表达式为: A B C D F 0 0 0 0 0 F=∑(5,6,7,8,9) 0 0 0 0 +∑φ(10,11,12,13,14,15) 0 0 0 0 0 0 0 0 0 0 0 0 AB CD 00 01 11 10 0 0 1 0 1 00 8 0 0 01 5 9 BD 1 1 11 0 中 BC 0 10 6 F=BD+BC+A φ
Φ Φ Φ Φ Φ Φ 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 A B C D F 真值表 由真值表列出F 的逻辑表达式为: F =∑(5, 6, 7, 8, 9) +∑φ(10,11,12,13,14,15) F = BD+BC+A 6 Φ Φ 7 Φ Φ 5 Φ 9 Φ 8 BD A BC AB CD 00 01 11 10 00 01 11 10

3考虑级数的逻辑设计 ·当逻辑电路的级数增多时,由于传输延迟时间增 大,以致造成电路的工作速度不能满足要求。此时应 设法压缩电路的级数,且使其在满足速度要求的前提 下最简: ·当电路要求门电路的扇入系数或扇出系数超出现 有组件的技术指标时,应采用增加电路级数的办法, 并使所设计的电路在满足现有组件的扇入或扇出系数 的前提下为最简: ●压缩级数和增加级数的设计思想是互斥的
3 考虑级数的逻辑设计 ● 当逻辑电路的级数增多时,由于传输延迟时间增 大,以致造成电路的工作速度不能满足要求。此时应 设法压缩电路的级数,且使其在满足速度要求的前提 下最简; ● 当电路要求门电路的扇入系数或扇出系数超出现 有组件的技术指标时,应采用增加电路级数的办法, 并使所设计的电路在满足现有组件的扇入或扇出系数 的前提下为最简; ● 压缩级数和增加级数的设计思想是互斥的

[例121 用与非门、与或非门分别实现以下函数: F=AB+AC 解:方案①对上式进行变换得: F=AB +AC F ABXAC 方案② 如果先求出的最简“与或”表达式,再瘫 求反, 则可求得级数最少的F。即 F=AB+AC=AB+AC 则 F=AB+AC 据此画出电路逻辑图,电路的级数最少。该方法称为 求反压缩法,仅适用于反函数较简单的情况
[例12] 用与非门、与或非门分别实现以下函数: F = AB + AC 据此画出电路逻辑图,电路的级数最少。该方法称为 求反压缩法,仅适用于反函数较简单的情况。 则 方案② 如果先求出 的最简“与或”表达式,再对 求反, 则 可求得级数最少的F 。即 解:方案① 对上式进行变换得: F = AB + A C F = AB ×A C F F F = AB + AC = AB + AC F = AB + AC