公式化简法 反复利用逻辑代数的基本公式、常用公式和运算 规则进行化简,又称为代数化简法。 必须依赖于对公式和规则的熟练记忆和一定的经 验、技巧。 (1)A·1=A (2)A+0=A 01律 (3)A·0=0 (4)A+1=1 交换律 (5)A·B=B·A (6)A+B=B+A 结合律 (7)A·(B·C)=(A·B)·C (8)A+(B+C)=(A+B)+C 分配律 (9)A·(B+C)=A·B+A·C (10)A+(BC)=(A+B)(A+C) 互补律 (11)A·A=0 (12)A+A=1 重叠律 (13)A·A=A (14)A+A=A 反演律 (15)AB=A+B (16)A+B=A·B 还原律 (17)A=A
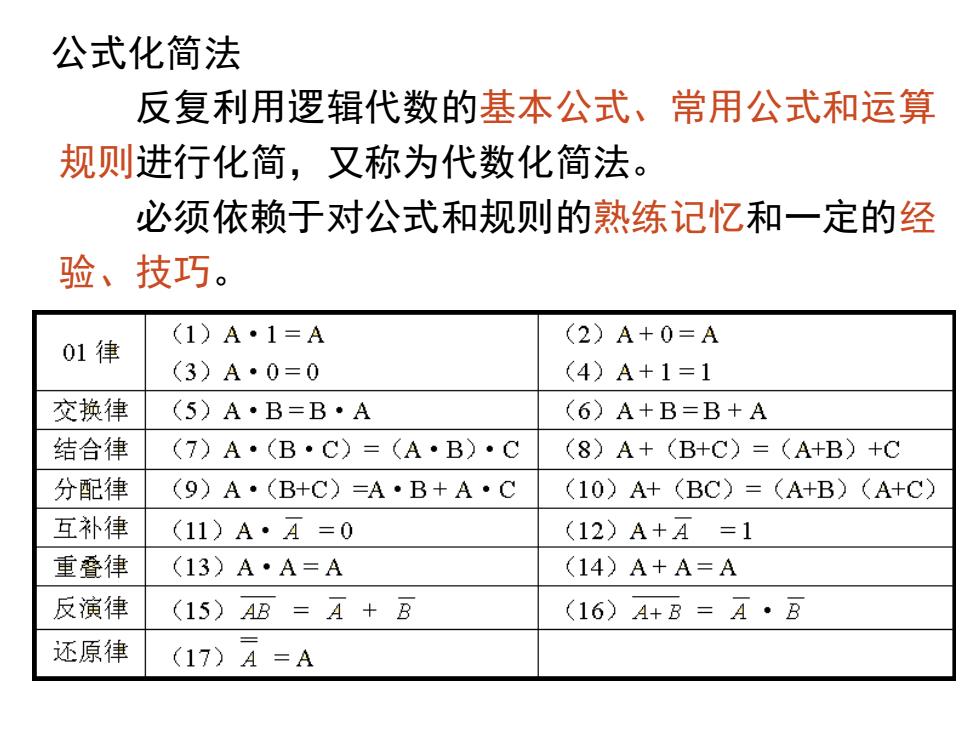
公式化简法 反复利用逻辑代数的基本公式、常用公式和运算 规则进行化简,又称为代数化简法。 必须依赖于对公式和规则的熟练记忆和一定的经 验、技巧

常用公式 ①AB+AB=A ②A+AB=A 最常使用,特别 ③A+AB=A+B 需要熟练记忆! ④AB+AC+BC=AB+AC AB+4 C+BCDE=AB+4 C (1)代入规则 在任何一个逻辑等式(如F=W)中,如果将 等式两端的某个变量(如B)都以一个逻辑函数 (如Y=BC)代入,则等式仍然成立。这个规则就叫 代入规则。 在公式化简中大量应用!需灵活掌握
(1)代入规则 在任何一个逻辑等式(如 F=W )中,如果将 等式两端的某个变量(如B)都以一个逻辑函数 (如Y=BC)代入,则等式仍然成立。这个规则就叫 代入规则。 在公式化简中大量应用!需灵活掌握。 最常使用,特别 需要熟练记忆!

(2)反演规则一便于实现反函数。 (3)对偶规则一使公式的应用范围扩大一倍, 使公式的记忆量减小一倍。 反演变换: 对偶变换: “.”6+ “.”6+” 66+”. c0”→61 c61”→0”, c“0?”→c1 原变量→反变量 c13”→0” 反变量原变量
(2)反演规则-便于实现反函数。 (3)对偶规则-使公式的应用范围扩大一倍, 使公式的记忆量减小一倍。 反演变换: “﹒”→“﹢” “﹢”→“﹒” “0” → “1” “1” →“0” , 原变量→反变量 反变量→原变量 对偶变换: “﹒”→“﹢” “﹢”→“﹒” “0” → “1” “1” →“0

(1)并项法 利用公式A+A=1或公式AB+AB=A进行化简,通 过合并公因子,消去变量。 例化简函数Y=AB.C+AB.C 解:Y=A·B.C+AB.C=AB(C+C)=AB 例化简函数 代入规则 Y=A.B.C+A-B.C+A.B.C+A.B.C 解: Y=AB(C+C)+AB(C+C)=AB+AB=A 或: Y=AB+AB=A 代入规则
例 化简函数 Y = ABC + ABC 解: Y = ABC + ABC = AB(C +C) = AB 例 化简函数 解: Y = ABC + ABC + ABC + ABC Y = AB(C +C) + AB(C +C) = AB + AB = A 代入规则 (1)并项法 利用公式A+A=1或公式AB+AB=A进行化简,通 过合并公因子,消去变量。 Y = AB+ AB = A 或: 代入规则

(2)吸收法 利用公式A+AB=A进行化简,消去多余项。 例:化简函数Y=A·B+A·B·CD(E+F) 解:Y=AB±4B)CD(E+F)=AB 例 化简函数 Y=ABD+CD+ABCD(EF+EF) 解:Y=ABD+CD+ABCD(EF+EF) =ABD+CD
(2)吸收法 利用公式A+AB=A进行化简,消去多余项。 例: 化简函数 解: 例 化简函数 解: Y = AB + ABCD(E + F) Y = AB + ABCD(E + F) = AB Y = ABD +C D + ABC D(EF + EF) ABD C D Y ABD C D ABC D EF EF = + = + + ( + )

(3)消去法 利用公式A+AB=A十B进行化简,消去多余项。 例化简函数 例化简函数 Y=AB+AC+BC Y=ABCD(E+F)+EF 解: 解: Y=AB+AC+BC Y=ABCD(E+F)+EF =AB+(A+B)C ABCD(E+F)+E+F ABABC =ABCD+E+F =AB+C =ABCD +EF
例 化简函数 解: 例 化简函数 解: (3)消去法 利用公式A+AB=A+B进行化简,消去多余项。 Y = AB + AC + BC AB C AB ABC AB A B C Y AB AC BC = + = + = + + = + + ( ) Y = ABCD(E + F) + EF ABCD EF ABCD E F ABCD E F E F Y ABCD E F EF = + = + + = + + + = + + ( ) ( )

(4)配项法 在适当的项配上A+A=1进行化简。 例化简函数 Y=AB+BC+BC+AB 解:Y=AB+BC+BC+AB =AB+BC+(+C+C+C) =AB+BC+ABC+ABC+ABC+ABC =AB+BC+AC(B+B) =AB+BC+AC
例 化简函数 解: (4)配项法 在适当的项配上A+A=1进行化简。 Y = AB + BC + BC + AB AB BC AC AB BC AC B B AB BC ABC ABC ABC ABC AB BC A A BC AB C C Y AB BC BC AB = + + = + + + = + + + + + = + + + + + = + + + ( ) ( ) ( )

例化简函数 解1得:Y=AB+BC+BC+AB =AB+BC+AC 解2: Y=AB+BC+BC+AB -ABC+C)C+C+ ABC+ABC+ABC+ABC+BC+AB AC(B+B)+BC+AB =AC+BC+AB 藏牙臂日
例 化简函数 解2: AC BC AB AC B B BC AB ABC ABC ABC ABC BC AB AB C C A A BC BC AB Y AB BC BC AB = + + = + + + = + + + + + = + + + + + = + + + ( ) ( ) ( ) AB BC AC Y AB BC BC AB = + + 解1得: = + + + 问题:函数 答案都正确Y的结果不一样,哪一个解正确呢? !最简结果的形式是一样的,都为三 个与项,每个与项都为两个变量。表达式不唯一!

(5)添加项法 利用公式AB+AC+BC=AB+AC,先添加一项BC, 然后再利用BC进行化简,消去多余项。 例化简函数Y=A·B+BC+BC+AB 解:Y=AB+BC+BC+AB -AB+BC+BC+AB+C =AB+BC+AB+AC =AB+BC+AC
例 化简函数 解: (5)添加项法 利用公式AB+AC+BC=AB+AC,先添加一项BC, 然后再利用BC进行化简,消去多余项。 AB BC AC AB BC AB AC AB BC BC AB AC Y AB BC BC AB = + + = + + + = + + + + = + + + Y = AB+ BC + BC + AB

下面举一个综合运用的例子。 Y=AD+AD+AB+AC+BD+ACEF+BEF+DEFG 解: Y=AD+AD+AB+AC+BD+ACEF +BEF+DEFG +AB+XC+ACEF +(BD+BEF DEEG) =A+C+BD+BEF
下面举一个综合运用的例子。 Y = AD+ AD+ AB+ AC + BD+ ACEF + BEF + DEFG 解: A C BD BEF A AB AC ACEF BD BEF DEFG Y AD AD AB AC BD ACEF BEF DEFG = + + + = + + + + + + = + + + + + + + ( )