
卡诺图化简逻辑函数的原理 卡诺图化简逻辑函数的基本原理:每两个逻辑相邻项可合并成一项, 消掉一个变量。 例如:ABC+ABC=ABC+C=AB 【例】化简F=ABC+AB.C+ABC+ABC 解:先填写卡诺图如下图(a)所示 BC0四 BC 01 11 10 A 00 01 11 10 A 0 0 1 +多余圈 a图 b图 a图得F=BC+AC b图得F=BC+AC+ ◆多余项 由本题可得两个重要结论: ★取每个圈中对应的公共变量相与,即为化简后函数表达式的一个与项。 ★化简后的每个圈为一个与项,因而画圈时要保证圈数最少,且每个圈中 都必须至少有一个新1(其它圈未包含进去的,避免多余项的出现)
卡诺图化简逻辑函数的原理 卡诺图化简逻辑函数的基本原理:每两个逻辑相邻项可合并成一项 , 消掉一个变量。 例如: ABC + ABC = AB(C + C) = AB 【例】 化简 F = ABC + ABC + ABC + ABC 解:先填写卡诺图如下图(a)所示 A BC 00 01 11 10 0 1 1 1 1 1 a图 a图得 F = BC + AC b图得 F = BC + AC + AB A BC 00 01 11 10 0 1 1 1 1 1 b图 多余圈 多余项 由本题可得两个重要结论: ★取每个圈中对应的公共变量相与,即为化简后函数表达式的一个与项。 ★化简后的每个圈为一个与项,因而画圈时要保证圈数最少,且每个圈中 都必须至少有一个新1 (其它圈未包含进去的,避免多余项的出现)
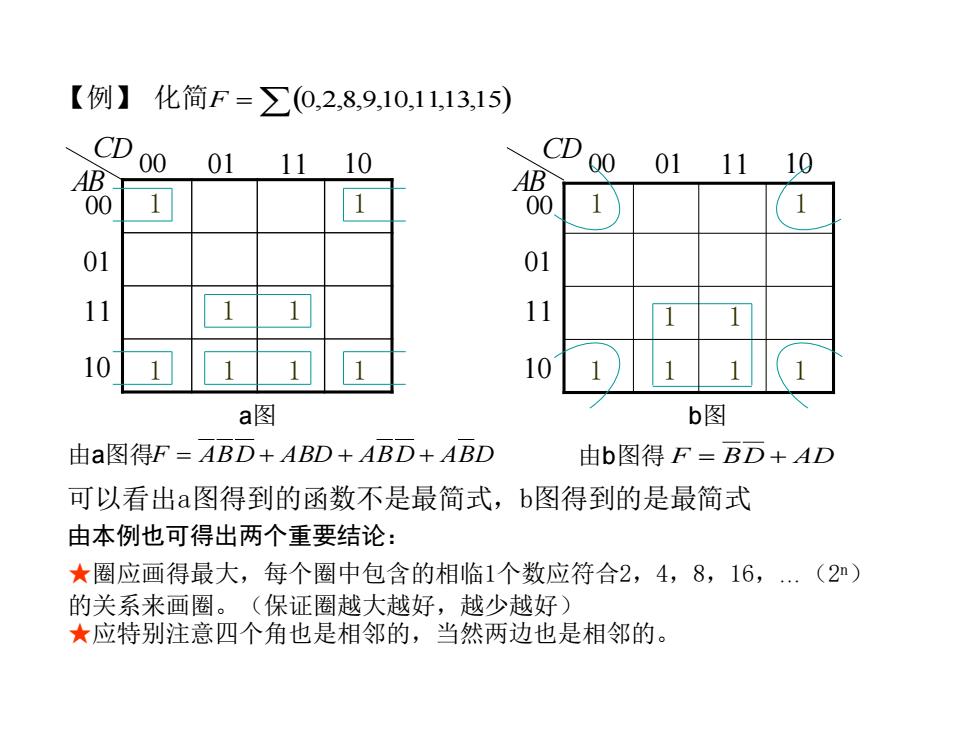
【例】化简F=∑(0,2,8,9,10,11,13,15) CD 00 01 11 10 CD 00 01 AB AB 1110 00 1 00 01 01 11 11 10 10 a图 b图 由a图得F=ABD+ABD+ABD+ABD 由b图得F=BD+AD 可以看出a图得到的函数不是最简式,b图得到的是最简式 由本例也可得出两个重要结论: ★圈应画得最大,每个圈中包含的相临1个数应符合2,4,8,16,.(2) 的关系来画圈。(保证圈越大越好,越少越好) ★应特别注意四个角也是相邻的,当然两边也是相邻的
【例】 化简 F =(0,2,8,9,10,11,13,15) 00 01 11 1000 01 11 10 AB CD 1 1 1 1 1 1 1 1 a图 10 10110100 00 01 11 D AB C 1 1 1 1 1 1 1 1 b图 由a图得 F = ABD + ABD + ABD + ABD 由b图得 F = BD + AD 可以看出a图得到的函数不是最简式,b图得到的是最简式 由本例也可得出两个重要结论: ★圈应画得最大,每个圈中包含的相临1个数应符合2,4,8,16,…(2 n) 的关系来画圈。(保证圈越大越好,越少越好) ★应特别注意四个角也是相邻的,当然两边也是相邻的

【例】化简F=∑0,123,4,5,6,8,9,10,11,12,13,14) 解:由最大数14知道这是个四变量函数,其卡诺图如下图所示,按上例中 的两个结论,可画出三个圈分别如图中所示,仔细检查,每个圈中都包含 有至少一个其它两个圈未包括进去的新1,故没有多余的圈。 CD 00 01 11 10 AB 00 1 01 1 1 1 11 1 1 1 10 1 F=B+C+D
【例】 化简 解:由最大数14知道这是个四变量函数,其卡诺图如下图所示,按上例中 的两个结论,可画出三个圈分别如图中所示,仔细检查,每个圈中都包含 有至少一个其它两个圈未包括进去的新1,故没有多余的圈。 F =(0,1,2,3,4,5,6,8,9,10,11,12,13,14) 1 1 1 1 1 1 1 1 1 1 1 1 1 1 AB CD 00 01 11 10 00011110 F = B +C + D