
1.化简的意义和最简单的概念 (1)化简的意义 例:用非门和与非门实现逻辑函数 Y=A+AB+ABC+BC+BC 解:直接将表达式变换成与非一与非式: Y=A+AB+ABC+BC+BC 两次求反 =A·AB·ABC.BC.BC 反演律 可见,实现该函数需要用两个非门、四个两输入 端与非门、一个五输入端与非门。电路较复杂。 & B B ×1 X2 X4 E
1.化简的意义和最简单的概念 (1)化简的意义 例:用非门和与非门实现逻辑函数 Y = A+ AB+ ABC + BC + BC 解:直接将表达式变换成与非-与非式: A AB ABC BC BC Y A AB ABC BC BC = = + + + + 可见,实现该函数需要用两个非门、四个两输入 端与非门、一个五输入端与非门。电路较复杂。 ×2 ×4 ×1 两次求反 反演律
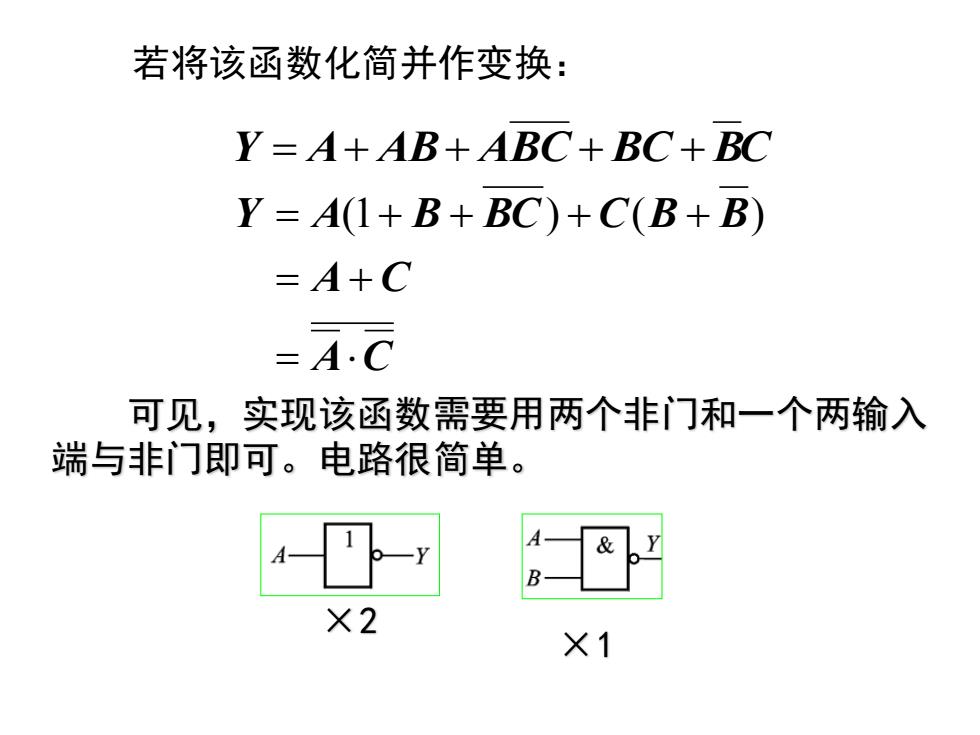
若将该函数化简并作变换: Y=A+AB+ABC+BC+BC Y=A(1+B+BC)+C(B+B) =4+C =A.C 可见,实现该函数需要用两个非门和一个两输入 端与非门即可。电路很简单。 X2 ×1
若将该函数化简并作变换: Y = A+ AB+ ABC + BC + BC A C A C Y A B BC C B B = = + = (1+ + ) + ( + ) 可见,实现该函数需要用两个非门和一个两输入 端与非门即可。电路很简单。 ×2 ×1

(2)逻辑函数的多种表达式形式 Y=AB+AC 与-或表达式 两次求反并用反演律 Y=AB.AC 与非-与非表达式 反演律 Y=(A+B)·(A+C) 或-与非表达式 反演律 Y-4+B+A+C 或非-或表达式
(2)逻辑函数的多种表达式形式 Y = AB+ AC Y = AB AC Y = (A+ B)(A+C) Y = A + B + A + C 与-或表达式 与非-与非表达式 或-与非表达式 或非-或表达式 两次求反并用反演律 反演律 反演律

(2)逻辑函数的多种表达式形式(续) Y-AA)4B+4C+BC =(A+C)(A+B) 或-与表达式 Y=4+C+4+B 或非或非表达式 Y=AC+AB 与-或非表达式 Y=AC.AB 与非-与表达式
(2)逻辑函数的多种表达式形式(续) 或-与表达式 或非-或非表达式 与-或非表达式 与非-与表达式 (A C)(A B) Y AA AB AC BC = + + = + + + Y = A+C + A + B Y = AC + AB Y = AC AB

由以上分析可知,逻辑函数有很多种表达式形 式,但形式最简洁的是与或表达式,因而也是最常 用的。 (3)逻辑函数的最简标准 由于与或表达式最常用,因此只讨论最简与或 表达式的最简标准。 最简与或表达式为: ①与项(乘积项)的个数最少; ②每个与项中的变量最少
由以上分析可知,逻辑函数有很多种表达式形 式,但形式最简洁的是与或表达式,因而也是最常 用的。 (3)逻辑函数的最简标准 由于与或表达式最常用,因此只讨论最简与或 表达式 的最简标准。 最简与或表达式为: ① 与项(乘积项)的个数最少; ② 每个与项中的变量最少