
组合逻辑设计 组合逻辑设计:是指组合逻辑电路的设计,它 是根据课题要求完成的逻辑功能,画出实现该 功能的逻辑电路。可见,它是组合逻辑分析的 逆过程。 组合逻辑设计的步骤 1.对逻辑问题进行数学描述。 2.进行逻辑函数的化简。 3.进行逻辑函数的变换。 4.画逻辑图,并考虑实际工程问题
组合逻辑设计 组合逻辑设计的步骤 1.对逻辑问题进行数学描述。 2.进行逻辑函数的化简。 3.进行逻辑函数的变换。 4.画逻辑图,并考虑实际工程问题。 组合逻辑设计 :是指组合逻辑电路的设计,它 是根据课题要求完成的逻辑功能,画出实现该 功能的逻辑电路。可见,它是组合逻辑分析的 逆过程

逻辑问题的描述 这一步的任务是:将设计问题转化为一个逻辑问题, 即用一个逻辑表达式来描述设计要求 。 逻辑问题描述的过程是 1.对事件的因果关系进行分析,将“因”定为输入变量 “果”定为输出逻辑函数 2.对逻辑变量赋值,用0,1分别表示两种不同状态 3.根据给定事件因果关系列出真值表,写出逻辑函数 表达式
逻辑问题的描述 这一步的任务是 :将设计问题转化为一个逻辑问题 , 即用一个逻辑表达式来描述设计要求 。 设计组合电路时,其设计要求往往以文字描述的形式 给出,是一个具有固定因果关系的事件。由文字描述的逻 辑问题直接写出逻辑函数是困难的,但列出真值表却比较 方便。 逻辑问题描述的过程是: 1. 对事件的因果关系进行分析,将“因”定为输入变量, “果”定为输出逻辑函数 2. 对逻辑变量赋值,用 0,1 分别表示两种不同状态; 3. 根据给定事件因果关系列出真值表 ,写出逻辑函数 表达式

逻辑问题的描述 [例4设计一个三人表决器。三人中多数赞同, 提案被通过;否则,提案不被通过。 多数表决器 解方案:厂赞同用“1表示 f(A,B,C) 不赞同用“0”表示 ↑1f A B C 通过用“"1”表示 、不通过用“0”表示 F=f(A,B,C) 列真值表: A 写出逻辑表达式: mi 0 0 0 0 0 F=∑(3,56,7) 1 0 0 1 0 2 0 1 0 0 =ABC+ABC+ABC +ABC 3 0 A N 1 4 0 0 0 结语:本例通过真值表列出逻辑表达式, 5 0 1 1 而真值表则是根据设计要求建立的。 6 1 1 0 1 7 1 1
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 A B C 0 0 0 1 0 1 1 1 0 1 2 3 4 5 6 7 mi F 列真值表: 逻辑问题的描述 [例4] 设计一个三人表决器。三人中多数赞同, 提案被通过;否则,提案不被通过。 解:方案: 通 过 用“1”表示 不通过 用“0”表示 赞 同 用“1”表示 不赞同 用“0”表示 写出逻辑表达式: ABC ABC ABC ABC F = + + + = (3,5,6,7) 多数表决器 f(A,B,C) A B C F F = f (A, B,C) 结语 : 本例通过真值表列出逻辑表达式, 而真值表则是根据设计要求建立的

[例 已知X=x1X2和Y=yy2是两个正整数,写出判别X>Y的逻辑表达式。 解:由题意知,X1X2>y2时,F=1 X1X2≤y1y2时,F=0 X>Y 比较x1X2和yy2,得简化真值表 (只包括F=1)如下: 判别逻辑 X1 2 y2 x2 yl y2 1 X 0 × 1 0 1 0 0 1 1 0 结语:本例通过简化真值表列出逻辑 表达式,而简化真值表是通过对设计要 求的分析建立的。 写出逻辑表达式为: F=X1y1+X1x2yiy2+x1xy1y2
[例5] 已知 X =x1x2 和Y =y1y2 是两个正整数,写出判别X >Y的逻辑表达式。 X >Y 判别逻辑 x1 x2 y1 y2 F 解:由题意知, x1x2 > y1y2 时,F=1 x1x2 ≤ y1y2 时,F=0 比较x1x2 和 y1y2 ,得简化真值表 (只包括 F=1)如下: 1 1 1 0 × 0 0 1 0 1 × 0 1 1 1 x1 x2 y1 y2 F 写出逻辑表达式为: F= x1y1+ x1x2 y1y2 + x1x2 y1y2 结语 :本例通过简化真值表列出逻辑 表达式,而简化真值表是通过对设计要 求的分析建立的

[例6]某民航客机的安全起飞装置在同时满足下列条件时,发 出允许滑跑信号:①发动机开关接通;②飞行员入座,且座位保 险带已扣上;③乘客入座,且座位保险带已扣上,或座位上无乘 客。试写出允许发出滑跑信号的逻辑表达式。 解:该装置的输入变量有: 发电机启动信呈S(发电机启动时S=1); 飞行员人座信号A(飞行员入座时A=1); 飞行员座位保险带已扣上信号B(飞行员座位保险带扣上时B=1 乘客座位状态信号Mi(有乘客时Mi=1,无乘客时Mi=0, i=l,2,3,…,n) 乘客座位保险带已扣上信号Nⅱ(乘客座位保险带扣上时Nⅱ=1, i=1,2,3,…,n)。 该装置的输出变量为F允许飞机滑跑条件满足时,F=1 该装置的逻辑组成框图如下:
[例6] 某民航客机的安全起飞装置在同时满足下列条件时,发 出允许滑跑信号:①发动机开关接通;②飞行员入座,且座位保 险带已扣上;③乘客入座,且座位保险带已扣上,或座位上无乘 客。试写出允许发出滑跑信号的逻辑表达式。 解 :该装置的输入变量有: 发电机启动信号 S(发电机启动时 S=1); 飞行员入座信号 A(飞行员入座时 A=1); 飞行员座位保险带已扣上信号 B(飞行员座位保险带扣上时B=1); 乘客座位状态信号 Mi(有乘客时Mi = 1 ,无乘客时 Mi = 0 , i =1,2,3,…,n); 乘客座位保险带已扣上信号 Ni(乘客座位保险带扣上时 Ni = 1, i =1,2,3,…,n)。 该装置的输出变量为 F(允许飞机滑跑条件满足时,F =1)。 该装置的逻辑组成框图如下:
安全起飞装置逻辑 f(S,A,B,Mi,N) 逻辑表达式为: S A BM MN N F=f(S,A,B,Mi,N) =S X4XBXM N+M)XM2N2 +M2).(M,N,+M) =SA邓BN,+M1)XN2+M2)…(Nn+Mn) 结语:本例中逻辑表达式是通过对设计要求的分析直接列出 的,既不通过真值表,也不通过简化真值表
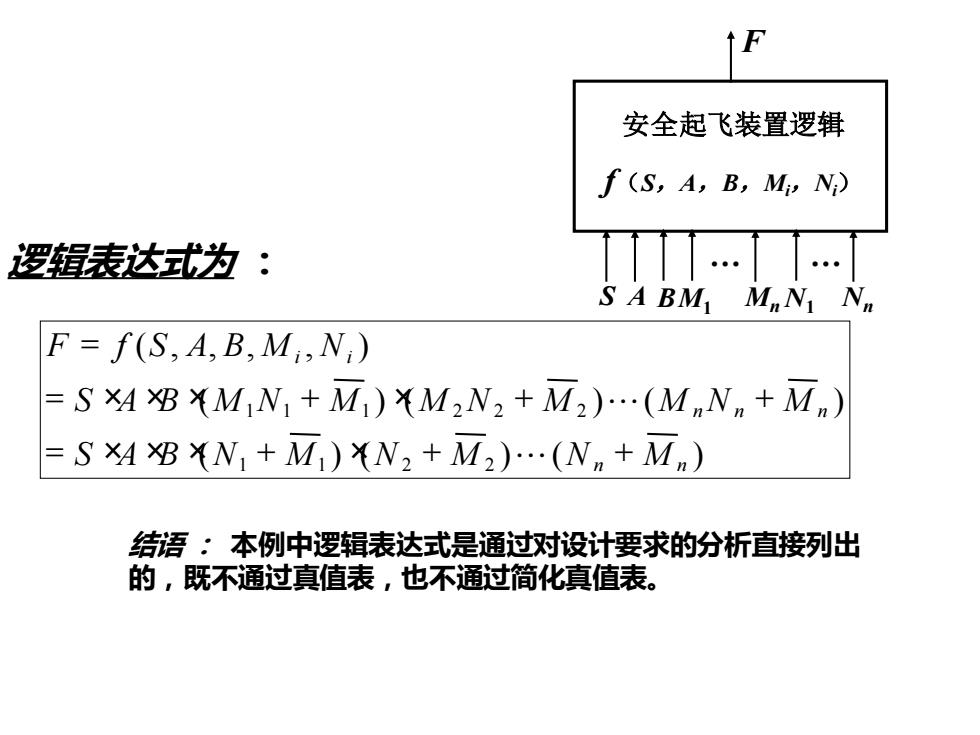
安全起飞装置逻辑 f(S,A,B,Mi,Ni) S A BM1 Mn N1 Nn F 逻辑表达式为 : … … ( ) ( ) ( ) ( ) ( ) ( ) ( , , , , ) 1 1 2 2 1 1 1 2 2 2 n n n n n i i S A B N M N M N M S A B M N M M N M M N M F f S A B M N = × × × + × + + = × × × + × + + = L L 结语 : 本例中逻辑表达式是通过对设计要求的分析直接列出 的,既不通过真值表,也不通过简化真值表

逻辑函数的变换 1.逻辑函数的“与非”门实 例7)用“与非”门实现逻辑函数F=AB+BC十CD十DA 解:对F两次求反,可得 F=AB+BC十CD+DA=AB·BC·CD·DA 对F三次求反,可得可用卡诺图直接求反) F=AB+BC+CD+DA=ABCD +ABCD F=ABCD+ABCD =ABCDABCD 结语:原函数较简单时,采用对Γ两次求反可节省门电路;当反函数较 简单时,采用对F三次求反可节省门电路。而前者可获得较高的传输速 度
逻辑函数的变换 结语 :原函数较简单时,采用对F两次求反可节省门电路;当反函数较 简单时,采用对F三次求反可节省门电路。而前者可获得较高的传输速 度。 1.逻辑函数的“与非”门实 现 解 :对 F 两次求反,可得 F =AB+BC +CD +DA = AB · BC · CD · DA 对 F 三次求反,可得 (可用卡诺图直接求反) F =AB+BC +CD +DA =A B C D +ABCD F = A B C D +ABCD = A B C D · ABCD [例7] 用“与非”门实现逻辑函数 F =AB+BC +CD +DA

2.逻辑函数的“或非”门实现 [例8]用“或非”门实现逻辑函数 F=AB十BC十CA 解:先求出F的对偶函数F的最简“与-或”表达式: F=(A+B)(B+C)(C+A)=ABC+ABC 再将F的最简“与-或”表达式变换为“与非与非”表达式: F'=ABC·ABC 对F求对偶,则得 F=(A十B+C)+(A+B+C)
2.逻辑函数的“或非”门实现 [例8] 用“或非”门实现逻辑函数 F =AB+BC +CA 解 : 先求出 F 的对偶函数F′的最简“与-或”表达式: F ′ =(A + B)(B + C )(C + A)= ABC + A B C 对F ′求对偶,则得 F = (A + B + C )+( A + B + C ) 再将F ′的最简“与-或”表达式变换为“与非-与非”表达式: F ′ = ABC · A B C

3.逻辑函数的“与或非”门实现 [例9]用“与或非”门实现逻辑函数 F=AB十BC+CA 解:(1)对F两次求反,可得 F=AB十BC十CA (2)对F一次求反(可用卡诺图直接求反),可得 F=AB+BC+CA=ABC+ABC F=F=ABC十ABC 比较二法,显然后者所得结果比前者简单
3.逻辑函数的“与或非”门实现 比较二法,显然后者所得结果比前者简单。 [例9] 用“与或非”门实现逻辑函数 F =AB+BC +CA 解 : (1)对 F 两次求反,可得 F = AB+BC +CA (2)对 一次求反(可用卡诺图直接求反),可得 F = AB+BC +CA = A B C + ABC F = F = A B C + ABC F