
1.最小项及最小项表达式 (1)最小项 设A、B、C是三个逻辑变量,若由这三个逻辑变 量按以下规则构成乘积项: ①每个乘积项都只含三个因子,且每个变量都是 它的一个因子; ②每个变量都以反变量(A、B、C)或以原变量(A、 B、C)的形式出现一次,且仅出现一次。 具备以上条件的乘积项共八个,我们称这八个乘 积项为三变量A、B、C的最小项。 AB是变量函数鲛量攸项順变量和反变量两种形式, 闺此是变量教的最顶鹅?
1.最小项及最小项表达式 (1)最小项 具备以上条件的乘积项共八个,我们称这八个乘 积项为三变量A、B、C的最小项。 设A、B、C是三个逻辑变量,若由这三个逻辑变 量按以下规则构成乘积项: ①每个乘积项都只含三个因子,且每个变量都是 它的一个因子; ②每个变量都以反变量(A、B、C)或以原变量(A、 B、C)的形式出现一次,且仅出现一次。 AB是三变量函数的最小项吗? ABBC是三变量函数的最小项吗? 推广:一个变量仅有原变量和反变量两种形式, 因此N个变量共有2 N个最小项
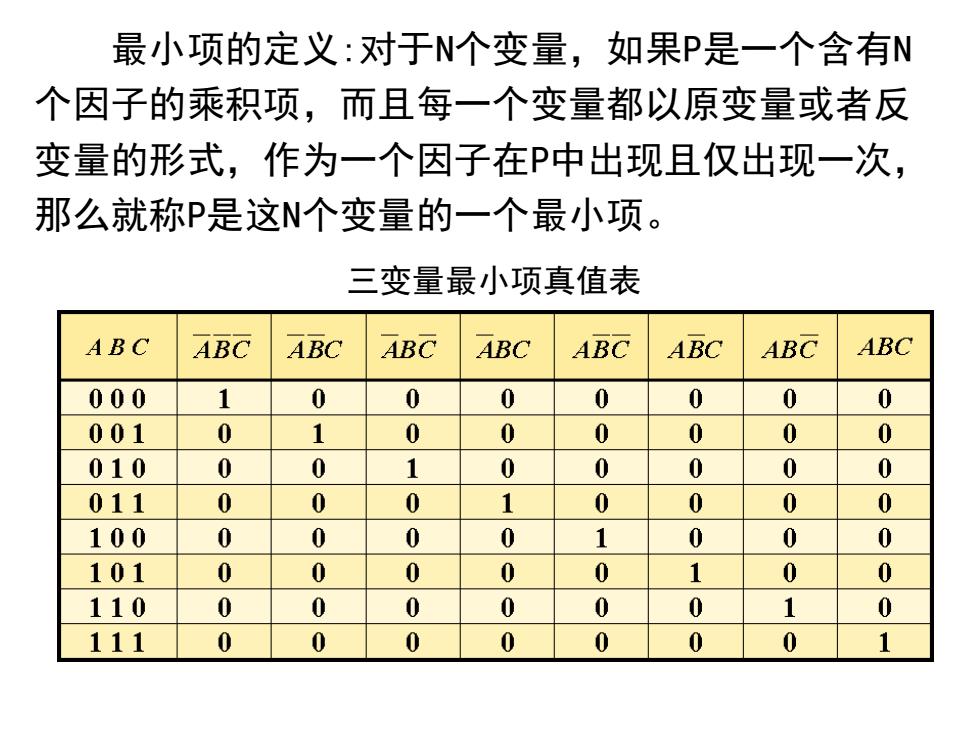
最小项的定义:对于N个变量,如果P是一个含有N 个因子的乘积项,而且每一个变量都以原变量或者反 变量的形式,作为一个因子在P中出现且仅出现一次, 那么就称P是这N个变量的一个最小项。 三变量最小项真值表 ABC ABC ABC ABC ABC ABC ABC ABC ABC 000 1 0 0 0 0 0 0 0 001 0 1 0 0 0 0 0 0 010 0 0 1 0 0 0 0 0 011 0 0 0 1 0 0 0 0 100 0 0 0 0 1 0 0 0 101 0 0 0 0 0 1 0 0 110 0 0 0 0 0 0 1 0 111 0 0 0 0 0 0 0 1
最小项的定义:对于N个变量,如果P是一个含有N 个因子的乘积项,而且每一个变量都以原变量或者反 变量的形式,作为一个因子在P中出现且仅出现一次, 那么就称P是这N个变量的一个最小项。 三变量最小项真值表
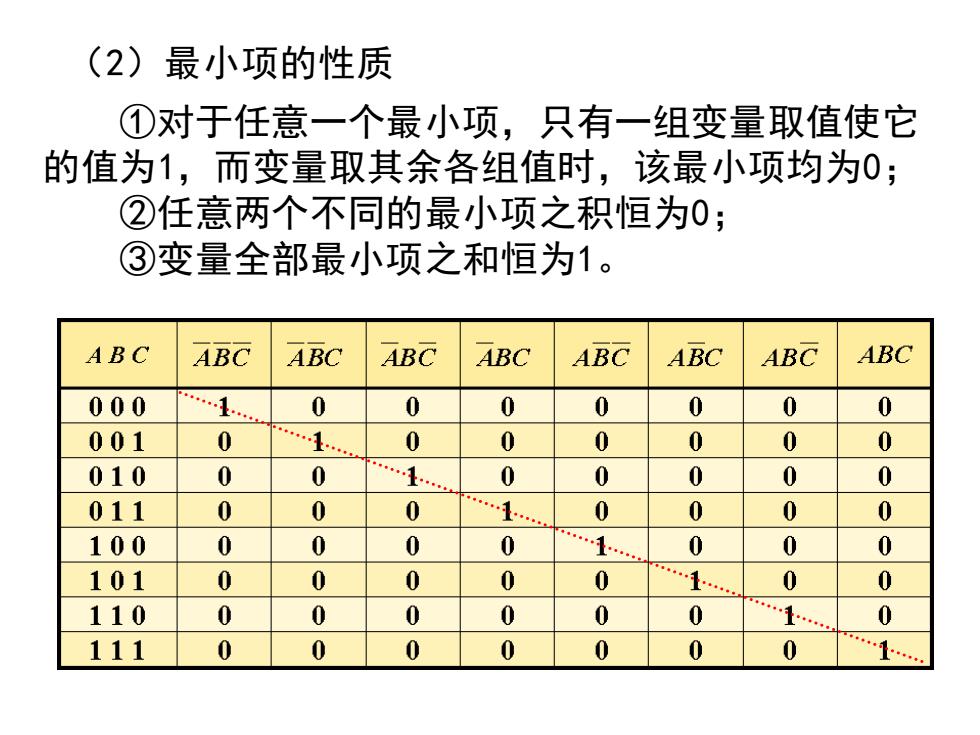
(2)最小项的性质 ①对于任意一个最小项,只有一组变量取值使它 的值为1,而变量取其余各组值时,该最小项均为0; ②任意两个不同的最小项之积恒为0; ③变量全部最小项之和恒为1。 ABC ABC ABC ABC ABC ABC ABC ABC ABC 000 0 0 0 0 0 0 0 001 0 0 0 0 0 0 0 010 0 0 …1 0 0 0 0 0 011 0 0 0 0 0 0 0 100 0 0 0 0 0 0 0 101 0 0 0 0 0 … 0 0 110 0 0 0 0 0 0 … 0 111 0 0 0 0 0 0 0
(2)最小项的性质 ①对于任意一个最小项,只有一组变量取值使它 的值为1,而变量取其余各组值时,该最小项均为0; ②任意两个不同的最小项之积恒为0; ③变量全部最小项之和恒为1
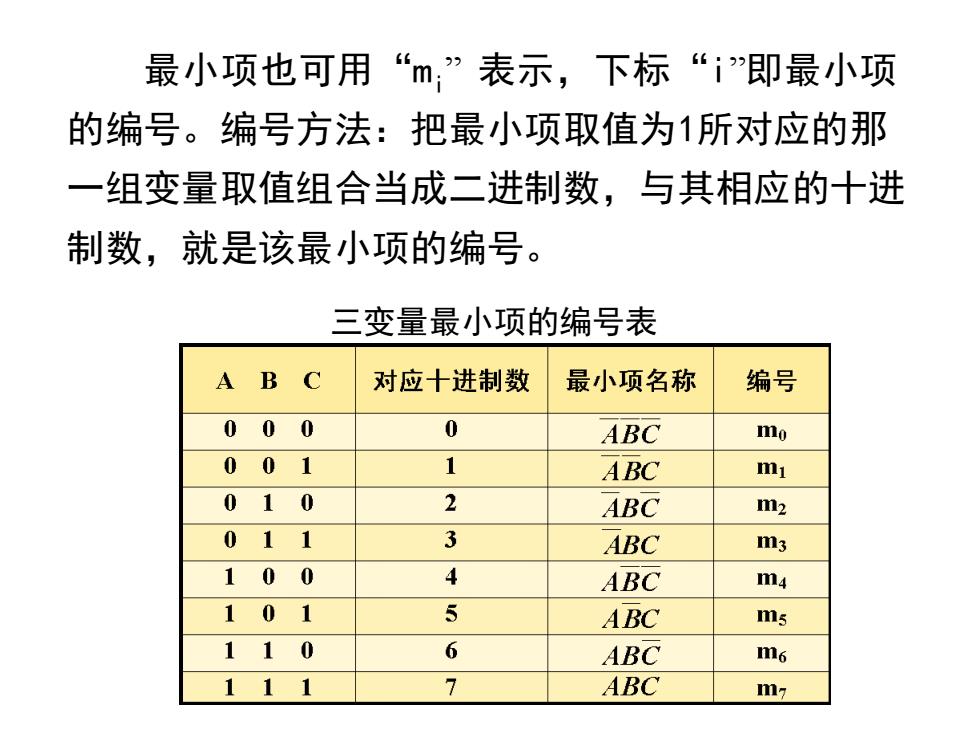
最小项也可用“m”表示,下标“i即最小项 的编号。编号方法:把最小项取值为1所对应的那 一组变量取值组合当成二进制数,与其相应的十进 制数,就是该最小项的编号。 三变量最小项的编号表 AB C 对应十进制数 最小项名称 编号 000 0 ABC mo 001 1 ABC mi 010 2 ABC m2 011 3 ABC m3 100 4 ABC m4 101 6 ABC ms 110 6 ABC m6 111 7 ABC m7
最小项也可用“ mi ” 表示,下标“i”即最小项 的编号。编号方法:把最小项取值为1所对应的那 一组变量取值组合当成二进制数,与其相应的十进 制数,就是该最小项的编号。 三变量最小项的编号表

(3)最小项表达式 任何一个逻辑函数都可以表示为最小项之和的 形式一标准与或表达式。而且这种形式是惟一的, 就是说一个逻辑函数只有一种最小项表达式。 例将Y=AB+BC展开成最小项表达式。 解:Y=AB+BC=AB(C+C)+(A+A)BC ABC+ABC+ABC 或:Y(A,B,C)=3+m6+m7 =∑m(3,6,7)
(3)最小项表达式 任何一个逻辑函数都可以表示为最小项之和的 形式——标准与或表达式。而且这种形式是惟一的, 就是说一个逻辑函数只有一种最小项表达式。 例 将Y=AB+BC展开成最小项表达式。 解: ABC ABC ABC Y AB BC AB C C A A BC = + + = + = ( + ) + ( + ) = = + + (3,6,7) ( , , ) 3 6 7 m 或: Y A B C m m m