江西农业大学：《数字逻辑》课程教学资源（PPT讲稿）第三章 布尔代数与逻辑函数化简——3.1 基本公式与规则 3.1.1 基本公式

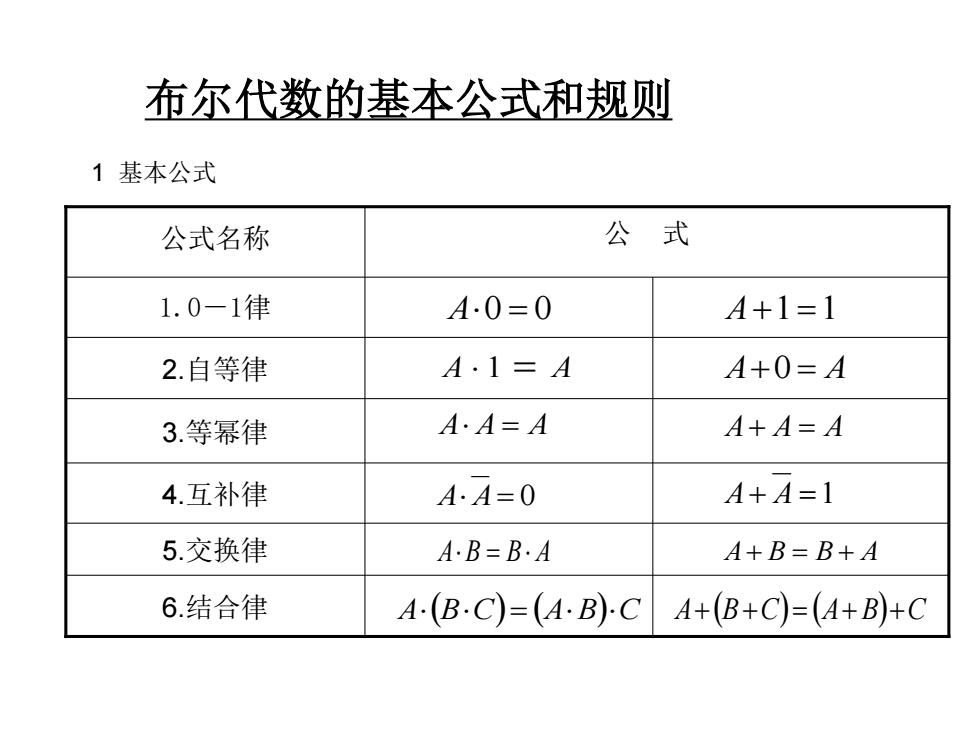
布尔代数的基本公式和规则 1基本公式 公式名称 公式 1.0-1律 A0=0 A+1=1 2.自等律 A·1=A A+0=A 3.等幂律 A·A=A A+A=A 4.互补律 A·A=0 A+A=1 5.交换律 AB=B·A 4+B=B+A 6结合律 4-(B-C)=(4-B)-C 4+(B+C)=(4+B)+C

布尔代数的基本公式和规则 1 基本公式 6.结合律 5.交换律 4.互补律 3.等幂律 2.自等律 1.0－1律 公式名称 公 式 A0 = 0 A  1 = A A+1 =1 A+0 = A A A = A A+ A = A A A= 0 A+ A =1 AB = B A A+ B = B + A A(BC) = (AB)C A+(B+C) = (A+ B)+C

7.分配律 A.(B+C)=AB+AC 4+BC=(4+B(4+C) 8.吸收律1 (A+B)(A+B)=A AB+AB=A 9.吸收律2 4(4+B)=A A+AB=A 10.吸收律3 4(+B)=AB A+AB=A+B 11.多余项定律 (4+BX4+CX(B+C)=(4+BX4+C)AB+AC+BC=AB+AC 12.求反律 AB=A+B 4+B=A.B 13.否否律 7-4

13.否否律 12.求反律 11.多余项定律 10.吸收律3 9.吸收律2 8.吸收律1 7.分配律 A(B+C) = AB+ AC A+ BC = (A+ B)(A+C) (A+ B)(A+ B) = A AB + AB = A A(A+ B) = A A+ AB = A A+ AB = A+ B (A+ B)(A+C)(B +C) = (A+ B)(A+C) A(A+ B)= AB AB+ AC + BC = AB+ AC AB = A+ B A+ B = AB A = A

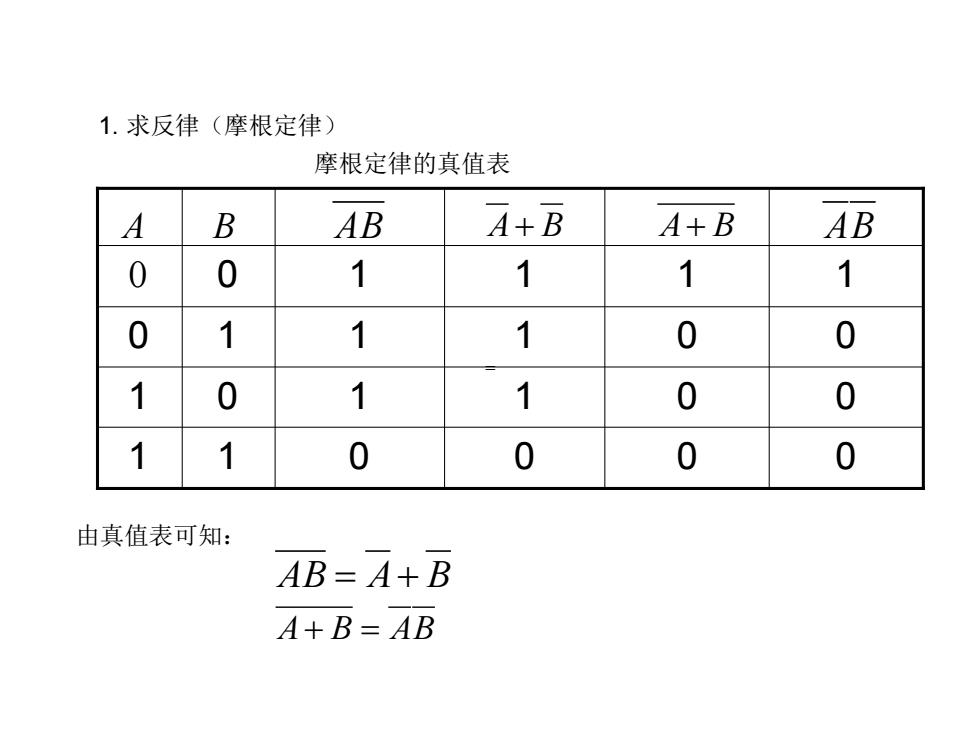
1.求反律（摩根定律） 摩根定律的真值表 B AB A+B 4+B AB 0 0 1 1 1 1 1 1 1 0 0 0 1 1 0 0 1 0 0 0 0 由真值表可知： AB=4+B A+B=AB

摩根定律的真值表 1. 求反律（摩根定律） 由真值表可知： 1 1 0 0 0 0 1 0 1 1 0 0 0 1 1 1 0 0 0 0 1 1 1 1 A B AB A+ B A+ B AB = AB = A+ B A+ B = AB

2.多余项定律 常用的为表2.1中的后一种形式，即 AB+AC+BC=AB+AC 它的正确性可用基本公式中的A+A=1A+1=1来证明 证明： 左端=AB+AC+BC·I=AB+AC+BC.(A+A =AB+AC+ABC+ABC (AB+ABC)+AC+ABC =AB(1+C)+AC(1+B) 二AB+AC=右端即 AB+AC+BC=AB+AC

2. 多余项定律 常用的为表2.1中的后一种形式，即 AB+ AC + BC = AB+ AC 它的正确性可用基本公式中的 A+ A =1 A+1 =1 来证明 证明： 左端 =AB+ AC + BC 1=AB + AC + BC (A + A) =AB+ AC + ABC + ABC =(AB + ABC) + (AC + ABC) = AB(1+ C)+ AC(1+ B) = AB + AC= 右端即 AB+ AC + BC = AB+ AC

在基本公式中，我们应当牢记以下几个常用结论： ●1加任何变量，结果都为1；0乘任何变量，结果都为0： 多个同一变量的和仍然是它本身，例如：A十A+··+A=A 多个同一变量的积仍然是它本身，例如：A·A…A=A ●同一变量的原变量与反变量之和恒为1，例如：x+x=1 同一变量的原变量与反变量之积恒为0，例如：x·x=O 摩根定律：AB=A+B 4+B =A.B ●A+AB=A+BAB+AC+BCD·=AB+AC 这两个公式也应牢记

在基本公式中，我们应当牢记以下几个常用结论： ● 1加任何变量，结果都为1；0乘任何变量，结果都为0。 ● 多个同一变量的和仍然是它本身，例如： A + A +  + A = A 多个同一变量的积仍然是它本身，例如： A A A = A ●同一变量的原变量与反变量之和恒为1, 例如： 同一变量的原变量与反变量之积恒为0，例如： x + x =1 x  x = 0 ● 摩根定律： AB = A + B A + B = A B ● A + AB = A + B AB+ AC + BCD = AB+ AC 这两个公式也应牢记