
第一章习题(作业)解答 4.将下列十进制数转换为二进制数: (1)35.625 (2)0.4373 解:(1)35.625=100011.101 (2)0.4373=0.0111 5.将下列二进制数转换为十进制数 (1)11000101(2)0.01001 (3)1010101.101 解:(1)11000101=197(2)0.01001=0.28(3)1010101.101=85.625 6.将下列十进制数转换为八进制数: (1)548.75 (2)100 解:(1)548.75=1044.6 (2)100=144 7.将下列八进制数转换为十进制数 82287 (2)(207.5)。=135.625 8.将下列十进制数转换为十六进制数: 解010-2376125 (1)100 (2)376.125=178.2 9.将下列十六进制数转换为十进制数: (1)(78.8)H (2)(3AF.E)H 解:(1)(78.8)H=120.1 (2)(3AF.E)H=943.875 10将下列二进制数分别用八进制数和十六进制数表示: (1)1010010 (2)110111101.10101 解:(1)1010010=(52)16=(112)8 (2)110111101.10101=(1BD.A1)16=(635.51)8 15.求下列BCD码代表的十进制数: (1)(100001110101.10010011)8421BCD(2)(100001110101.10010011)余3BcD 解:(1)(100001110101.10010011)8421BcD=875.93(2)(100001110101.10010011)余 3BCD=542.60 16.将下列8421BCD码转换成二进制数: (2)00111000 (2)00111000(38)10=1001102 17.求下列二进制代码的奇偶校验位: 保10位为A10818 3)1111110 2)校验位为0(③)校验位为1 18实现如下代码转换 (1)(1011.1110)2421BcD (2)(1000.1011)5421BcD 解(1)(1011.1110)2421BcD1000.1011)余3BcD(2) (1000.1011)5421BcD-=(0101.1000)421BCD
第一章习题(作业)解答 4. 将下列十进制数转换为二进制数: (1) 35.625 (2) 0.4373 解:(1) 35.625=100011.101 (2) 0.4373=0.0111 5. 将下列二进制数转换为十进制数 (1) 11000101 (2) 0.01001 (3) 1010101.101 解: (1) 11000101=197 (2) 0.01001=0.28 (3) 1010101.101=85.625 6.将下列十进制数转换为八进制数: (1)548.75 (2)100 解:(1)548.75=1044.6 (2)100=144 7. 将下列八进制数转换为十进制数 (1) (376.2)o (2) (207.5)o 解: (1) (376.2)o=254.25 (2) (207.5)o=135.625 8. 将下列十进制数转换为十六进制数: (1) 100 (2) 376.125 解: (1) 100=64 (2) 376.125=178.2 9. 将下列十六进制数转换为十进制数: (1) (78.8)H (2) (3AF.E)H 解: (1) (78.8)H=120.1 (2) (3AF.E)H=943.875 10.将下列二进制数分别用八进制数和十六进制数表示: (1)1010010 (2)110111101.10101 解:(1)1010010=(52)16=(112)8 (2)110111101.10101=(1BD.A1)16=(635.51)8 15. 求下列 BCD 码代表的十进制数: (1) (100001110101.10010011)8421BCD (2) (100001110101.10010011)余 3BCD 解:(1) (100001110101.10010011)8421BCD= 875.93 (2) (100001110101.10010011)余 3BCD=542.60 16. 将下列 8421BCD 码转换成二进制数: (1) 01111001.011000100101 (2) 00111000 解: (1) 01111001.011000100101=(79.625)10 =(1001111.101)2 (2) 00111000=(38)10 =(100110)2 17. 求下列二进制代码的奇偶校验位: (1) 11010101 (2) 100100100 (3) 1111110 解: (1) 校验位为 1, (2) 校验位为 0 (3) 校验位为 1 18.实现如下代码转换: (1) (1011.1110)2421BCD (2) (1000.1011)5421BCD 解 (1) (1011.1110)2421BCD=(1000.1011)余 3BCD (2) (1000.1011)5421BCD=(0101.1000)8421BCD

第二章习题(作业)解答 1.二极管门电路如图2-35所示二极管具有理想导电特性。A、B的高电平输入为3V,低电平输入 为0.3V,分别列出图()、图b)的真值表,并写出输出函数表达式。 +5 (a) 6) 图2-35题1图 解:真值表如表(a)、b)所示 ABF 11 01 1 (6) 逻辑表达式品下 a)F=AB (b)F2=A+B 2.对应图2-36(a)的波形,画出图236(b)中各电路的输出波形
第二章习题(作业)解答 1.二极管门电路如图 2-35 所示.二极管具有理想导电特性。A、B 的高电平输入为 3V,低电平输入 为 0.3V,分别列出图(a)、图(b)的真值表,并写出输出函数表达式。 2. 对应图 2-36(a)的波形,画出图 2-36(b)中各电路的输出波形

常 图2-36题2 1) (2 (3) (4) 3.对应图2-37(a)所示波形,画出图2-37(b)、(c)的输出波形
3. 对应图 2-37(a)所示波形,画出图 2-37(b)、(c)的输出波形

-F 图2-3 (b)图直值表 A B F 0 高阻 0 10 解:(c)图为三态0c门,可参考(b)图的解,详解略 x=5mA,10
4.某 TTL 门的 IOhmax=5mA, IOlmax20ma, 开门电平 UON=1.8V,关门电平 UOFF=0.8V。用该 TTL 门构 成的电路如图 2-38 所示。各个电路的输出函数表达式如下。判断这些表达式是否成立?并简述理 由

F1=BC⑦ F2=ABC而 F3=丽C而 F4=ABC而 Fs=AB+CD 巴 01 (a) ® (b) -F ≥1 3002 (c) 32 (e) 32 (d) 图2-38

格。樱不有手丹电意子圆不花不方式. 8不工A个平是要的限去水。 5.图239中各电路及其表达式是否有错?简述理由。图中所有的门电路均为标准系列。 解:本题解题的依据是灌电流和拉电流等条件米判断电路能否正常工作
解:(a)图连接不正确。由于 TTL 门电路采和推拉式输出方式,因此不能接成“线与”工作方式。 (b)图连接不正确。当 UOH= 3V 时,IOH= 3/150=0.02A=20ma>IOHmax, 输出电平逻辑不正常。 (c)图不正确。 多余端的处理不正确。电阻的阻值太小。 (d)图 IOH= 1mA< IOHmax,输出电平逻辑正常 (e)图正确,多余端的处理符合要求。 5. 图 2-39 中各电路及其表达式是否有错?简述理由。图中所有的门电路均为标准系列。 解:本题解题的依据是灌电流和拉电流等条件来判断电路能否正常工作
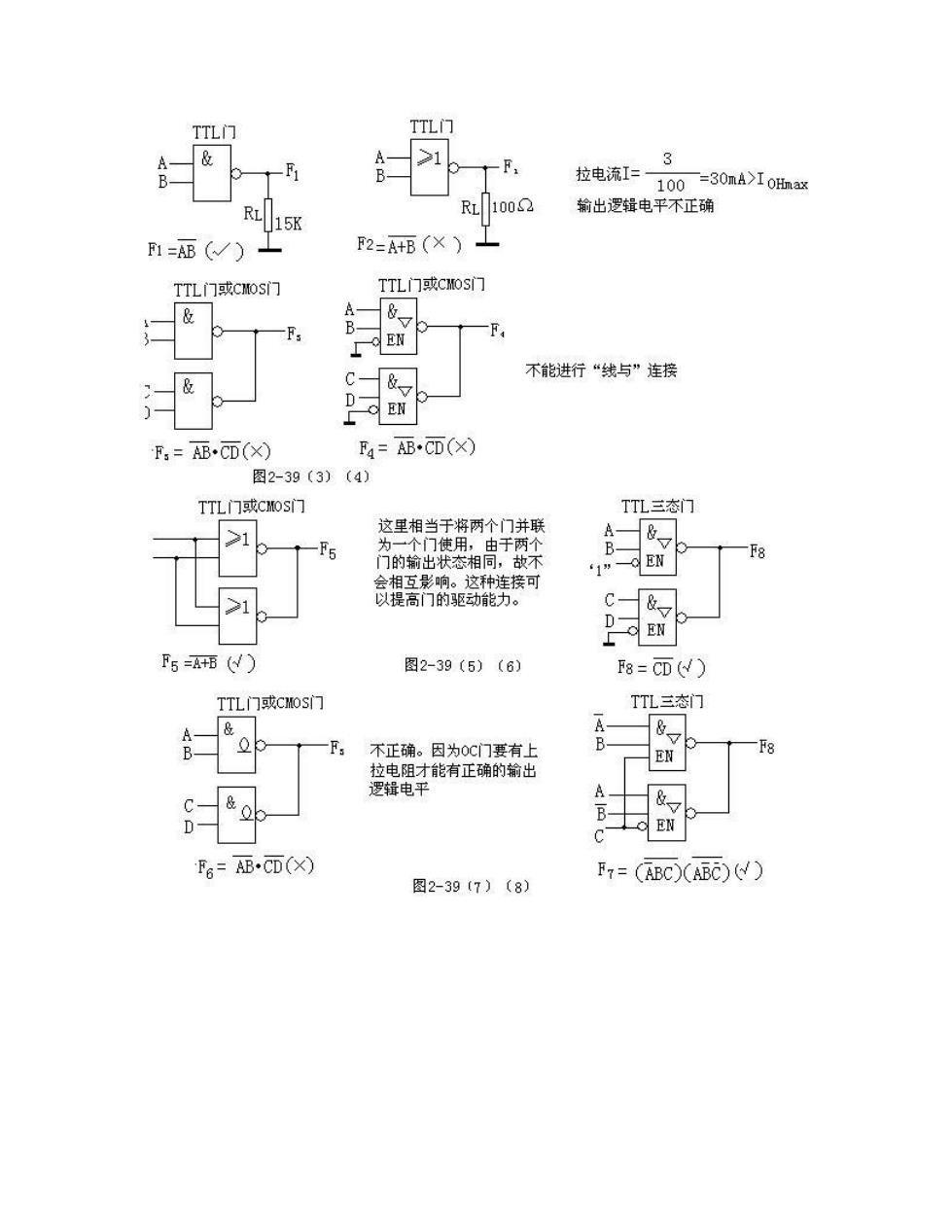
TTL门 TTL门 >1 3 -F, 拉电流I= 100 =30mA>IO R1002 输出逻辑电平不正确 m=B(√) F2=A+B(X)- TTL门或Cos TTL门或CMOs门 A C&。 不能进行“线与”连接 F=AB·CD(X) F4=AB·C⑦(X) 图2-39(3)(4) TTL门或C0S门 TTL三态门 这里相当于辉两个门并联 1 -Fc 门使用, 8 的 于两 相同 1男 EN >1 高门的驱接司 C-& 上w F5=( 图2-39(5)(6) F8=CD() TTL门或COS门 TTL三态门 A- F EN c-eol D F6=AB·C而(X) F7=(ABC)(ABC)) 图2-39(7)(8)

第三章习题(作业)解答 (3)列出输入三变量多数表决器的真值表。 (4)一位一讲制数加法申路。右三个入端 、B、C,它们分别为加数、被加数及由低位来的进 位位,有两个输出端S、C1分别表示输出和数及向更高位的进位数。 解) (2) ABICIE A B C S C网 A 01 .i F-ABC+ABC+ABC+ABC 适 P-ABC*ABC+ABC+ABC S-AEC4ABC+ABC+ABC :A©B9C C1-ABC+ABC4ABC+ABC 题3.1解 2.用真值表证明下列逻辑等式 (1)A+BC=(A+B)(A+C) (2)AB+AB+AB-A+B 证明 证明 A 00011 A B AB AB A+B 0001 0101010 001111 、d
第三章习题(作业)解答 1.列出下述问题的真值表,并写出逻辑表达式: (1)设三变量 A、B、C,当变量组合值中出现奇数个 1 时,F=1,否则为 0。 (2)设三变量 A、B、C,当输入端的信号不一致时,输出为 1,否则为 0。 (3)列出输入三变量多数表决器的真值表。 (4)一位二进制数加法电路,有三个输入端 A、B、C,它们分别为加数、被加数及由低位来的进 位位,有两个输出端 S、Ci+1 分别表示输出和数及向更高位的进位数。 2.用真值表证明下列逻辑等式:

(4)AB+AC=AB+AC 证明: (3)AB+AB+AB+AB=】 ABC AB AC AB+AC=AB+AC 证明: AB AB ABABAB 0: 988 01 0000001 1 3.写出下列函数的对偶式G及反函数F: (1)F=AB+CD (2)F=A+B+C+D+E 解:G=G+B(C+D)F=a)(C+D)=(A+B)(C+D) 解:G=ABCF=iBCD (3)F=AB配+G+BC)(A+C) 解:G=(a+B+C)aB+C)+aC F=A+B+C(A (B+C))+AC (4)F=(A+B+C)ABC=0 解:G=ABC+G+B+C)=1 F=ABC+(A+B+C)=1 (5)F=AB+CD+BC+D+CE+D+E 解:G=(a+B)C·(B+C)D(C+E)D F=G+B)C+而+C)D(C+)园 4.用公式证明下列各等式 (1)AB+AB=AB AB=(A+B)(A+B) 解:AB+AE=ABAB=(A+B)A+B)=右边,证毕 (2)ABC+ABC+ABC+ABC-ABOC 解:A(BC+B+A(BC+BC)=A(B⊙C)+A(B⊕C)=A⊕B⊕C证毕。 (3)ABC+ABC-AB+BC+CA 解:右边=AB BC CA=(AB+AC+BB+BC)·(C+A)=ABC+ABO=左边,证毕。 5.用逻辑代数公式,将下列函数化简成最简的与或”式:
3.写出下列函数的对偶式 G 及反函数 F: 4.用公式证明下列各等式 5.用逻辑代数公式,将下列函数化简成最简的“与或”式:

(1)F=ABC+A+B+C (2)F=AB+AC+BC+ABC+ABCD 解:利用求反律解 解:利用多余项定律求 F=ABC+ABC F-AB+ABC+AC+ABCD+BC-AB+AC+BC-AB+BC (3)F=AB+ABD+AC+BCD (4)F=(A田B)AB+AB+AB 解:F=AB+AC+BCD=AB+AC 解:(AB+AB)(ABAB)+AB=AB+AB (5)F=A(A+B)+B(B+C)+B (6)下=AB+AEBC+EC 解:AB+B+BC+B=AB+BC+B 解:下=AB+BC+AB+C-B=AB+BC AB+BC+B (C+C)=AB+BC+BC-B 6.用卡诺图将下列函数化简成最简“与或”式,并分别用与门、或门和与非门实现: (2)F=∑(0,1,3,4,5,7) 解:F=B+C ①化作与门形式=B+C=B 、B 00 01 11 0 1 ①1 1 ③用与非门实现F=B+C ②用或门实现:F=B+C F-B+C-B C 日-
6.用卡诺图将下列函数化简成最简“与或”式,并分别用与门、或门和与非门实现: (2)F=∑(0,1,3,4,5,7)