
第一章 第一方 映射与品数 映射 二、函数 HIGH EDUCATION PRESS 机动目录上页下页返回结束
第一章 一、映射 二、函数 第一节 机动 目录 上页 下页 返回 结束 映射与函数

一映射 引例 学生的集合 学号的集合 按一定规则查号 教室座位 学生的集合 的集合 按一定规则入座 +o HIGH EDUCATION PRESS 机动目录上页下页返回结束
学生的集合 学号的集合 按一定规则查号 学生的集合 教室座位 的集合 按一定规则入座 机动 目录 上页 下页 返回 结束 引例 一 . 映射

1定义设X,Y是两个非空集合,若存在一个对应规 则f,使得Vx∈X,有唯一确定的y∈Y与之对应,则 称f为从X到Y的映射,记作f:X→Y X 元素y称为元素x在映射f下的像,记作y=f(x) 元素x称为元素y在映射f下的原像 集合X称为映射f的定义域; Y的子集∫(X)={f(x)x∈X}称为f的值域 HIGH EDUCATION PRESS 机动目录上页下页返回结束
1.定义 设 X , Y 是两个非空集合, 若存在一个对应规 则 f , 使得 有唯一确定的 与之对应 , 则 称 f 为从 X 到 Y 的映射, 记作 f : X → Y . 元素 y 称为元素 x 在映射 f 下的 像 , 记作 y = f ( x ) . 元素 x 称为元素 y 在映射 f 下的 原像 . 集合 X 称为映射 f 的定义域 ; Y 的子集 f ( X ) = f ( x) x X 称为 f 的 值域 . X Y f 机动 目录 上页 下页 返回 结束

注意: 1)映射的三要素一 定义域,值域,对应规则 2)元素x的像y是唯一的, 但y的原像不一定唯一 HIGH EDUCATION PRESS 机动目录上页下页返回结束
注意: 1) 映射的三要素— 定义域 , 值域, 对应规则 . 2) 元素 x 的像 y 是唯一的, 但 y 的原像不一定唯一 . 机动 目录 上页 下页 返回 结束

容服 例1设f:R→R,对每个x∈R,f(x)=x2 显然,f是一个映射 定义域:D=R 值域:R={yy≥O} -2 0 MIGH EDUCATION PRESS
第一节 映射与函数 第一章 函数与极限 定义域: 值域:

例2设X={x,川x2+y=1 Y={(x,0)lx|≤1} f:X→Y.f是一个映射 定义域:Dr=X (化,y) 值域:Rr=Y (x,一y) 1 第GH EDUCATION PRESS
第一节 映射与函数 第一章 函数与极限 例2 设 定义域: 值域: 2 2 X x y x y = + = ( , ) | 1
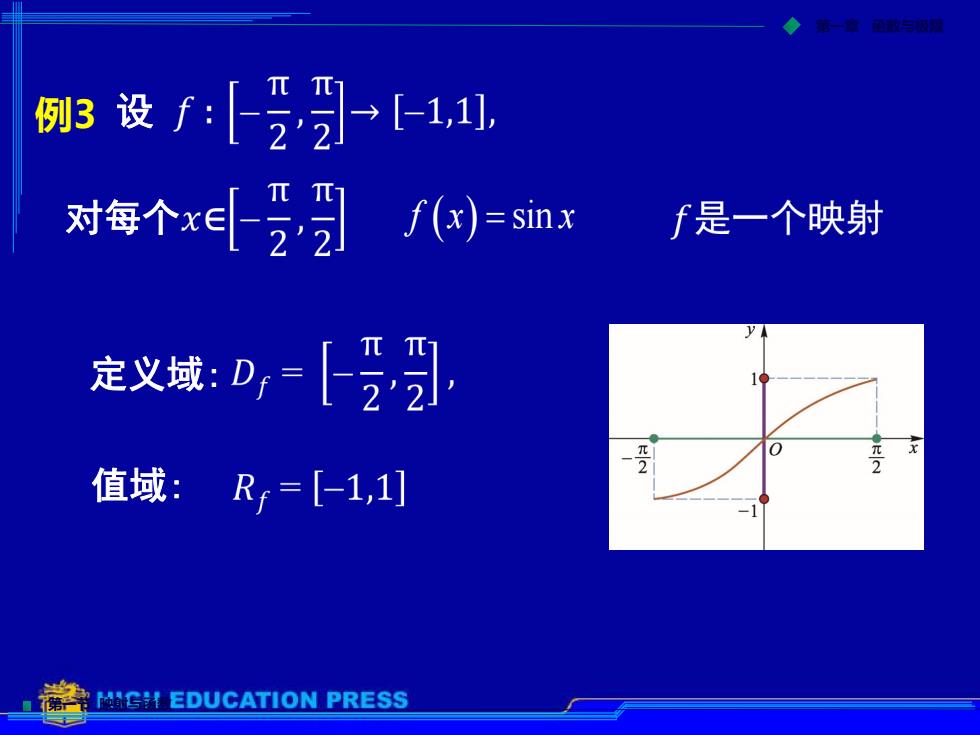
例3设f:习1, 对每个x习)smx f是一个映射 定义域:D【引 值域:Rj=[-1,1] MH EDUCATION PRESS
第一节 映射与函数 第一章 函数与极限 定义域: 值域: 例3 设 对每个 f x x ( ) = sin
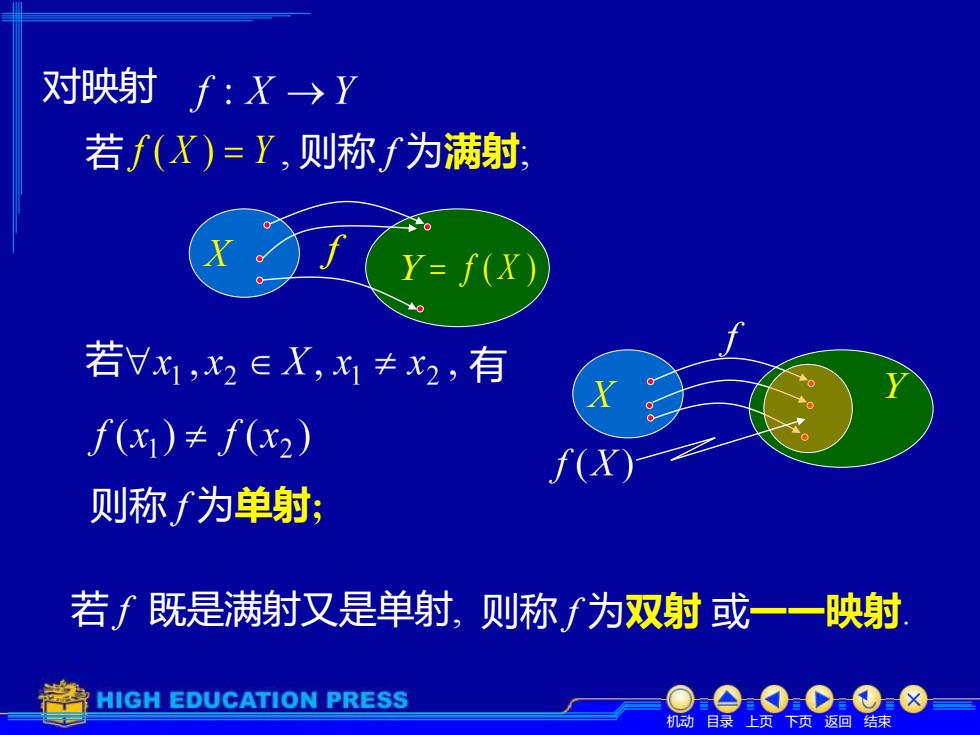
对映射f:X→Y 若f(X)=Y,则称f为满射 Y=f(X) 若Vx1,x2∈X,x1≠x2,有 f(x)≠f(x2) f(x 则称f为单射; 若∫既是满射又是单射,则称f为双射或一一映射 HIGH EDUCATION PRESS 机动目录上页下页返回结束
对映射 若 f ( X ) = Y , 则称 f 为满射; X Y f = f ( X ) 若 有 则称 f 为单射; 若 f 既是满射又是单射, 则称 f 为双射 或一一映射. X Y 机动 目录 上页 下页 返回 结束

映射又称为算子,在不同数学分支中有不同的名称 X 非空集X X上的泛函 数集Y 非空集X X上的变换 非空集Y 实数集X X上的函数 实数集Y MGH EDUCATION PRESS
第一节 映射与函数 第一章 函数与极限 非空集X 𝑓 Y 数集Y 非空集X 非空集Y 实数集X 实数集Y 注

2.逆映射与复合映射 (1)逆映射的定义 定义:若映射f:D→f(D)为单射,则存在一新映射 f:f(D)→D,使Vy∈f(D)f(y)=x,其中f(x)=y, 称此映射f为f的逆映射 习惯上,y=f(x),x∈D 的逆映射记成 y=f(x),x∈f(D) 例如,映射y=x2,x∈(-o,0],其逆映射为 y=-Vx,x∈[0,+o) HIGH EDUCATION PRESS 机动目 下页返回结束
2. 逆映射与复合映射 (1) 逆映射的定义 定义: 若映射 为单射, 则存在一新映射 使 习惯上 , y = f ( x), x D 的逆映射记成 ( ) , ( ) 1 y = f x x f D − 例如, 映射 其逆映射为 D f (D ) f −1 f 其中 称此映射 −1 f 为 f 的逆映射 . 机动 目录 上页 下页 返回 结束