
第二章材料在其他静载下的 力学性能 口本章的意义:材料在实际服役中的受力 形式和受力状态十分复杂,单向拉伸得到 的性能数据不能完全反映材料的变形、断 裂等特点。为了充分揭示材料的力学行为 和性能特点,常采用扭转、弯曲、压缩以 及带有台阶、孔洞、螺纹等与实际受力相 似的加载方式进行性能实验,为合理选材 和设计提供充分的实验依据
1 第二章 材料在其他静载下的 力学性能 ❑本章的意义:材料在实际服役中的受力 形式和受力状态十分复杂,单向拉伸得到 的性能数据不能完全反映材料的变形、断 裂等特点。为了充分揭示材料的力学行为 和性能特点,常采用扭转、弯曲、压缩以 及带有台阶、孔洞、螺纹等与实际受力相 似的加载方式进行性能实验,为合理选材 和设计提供充分的实验依据

第二章 材料在其他静载下的力学性能 口本章的内容: 介绍扭转、弯曲、压缩以及带缺口试 样的静拉伸以及材料硬度试验等试验方法 的特点、应用范围及其所测定的力学性能 指标。 (本章采用多媒体辅助教学) 2
2 第二章 材料在其他静载下的力学性能 ❑本章的内容: 介绍扭转、弯曲、压缩以及带缺口试 样的静拉伸以及材料硬度试验等试验方法 的特点、应用范围及其所测定的力学性能 指标。 (本章采用多媒体辅助教学)

第一节应力状态软性系数 口本章涉及到了实际受力状态,必须了解一些物 体在受力时应力状态分析的力学基础知识,因 为力学性能是研究材料受力以后的行为,首先 要知道材料的受力状态已经不是简单的一维应 力状态(如单向拉伸),而要扩展到二维、三 维。一些简单的公式,定律也要扩展到二维、 三维。应力应变也不是一般的表示,要用到矢 量、向量表示。本节简单介绍描述应力状态的 些重要参量、概念和公式。 3
3 第 一 节 应力状态软性系数 ❑本章涉及到了实际受力状态,必须了解一些物 体在受力时应力状态分析的力学基础知识,因 为力学性能是研究材料受力以后的行为,首先 要知道材料的受力状态已经不是简单的一维应 力状态(如单向拉伸),而要扩展到二维、三 维。一些简单的公式,定律也要扩展到二维、 三维。应力应变也不是一般的表示,要用到矢 量、向量表示。本节简单介绍描述应力状态的 一些重要参量、概念和公式

第一节应力状态软性系数 点的应力状态介绍 受力物体内的每一点上所受的力都使 这一物体点保持平衡,所以整个物体才处 于平衡状态。物体内每一点的受力状态不 完全相同。 4
4 第 一 节 应力状态软性系数 一、点的应力状态介绍 受力物体内的每一点上所受的力都使 这一物体点保持平衡,所以整个物体才处 于平衡状态。物体内每一点的受力状态不 完全相同

第一节应力状态软性系数 口为了分析问题方便,力学上研究物体的应 力应变状态时,(基本步骤) 1把物体置于x-y-z直角坐标系中; 2在所研究点的周围取与各坐标面平行的无 穷小的平行六面体,dx,dy,dz;将每一面 上作用的力分解为一个正应力和两个剪切 应力,且分别与三个坐标轴平行。 5
5 第 一 节 应力状态软性系数 ❑为了分析问题方便,力学上研究物体的应 力应变状态时,(基本步骤) 1 把物体置于x-y-z直角坐标系中; 2 在所研究点的周围取与各坐标面平行的无 穷小的平行六面体,dx,dy,dz;将每一面 上作用的力分解为一个正应力和两个剪切 应力,且分别与三个坐标轴平行

第一节应力状态软性系数 这样,在确定的坐标系中描述一个点的 应力状态,可用与坐标轴平行的小六面体上 的应力来表示。共9个应力分量,三个正应 力,六个剪应力(如图2-1所示)。 6
6 第 一 节 应力状态软性系数 这样,在确定的坐标系中描述一个点的 应力状态,可用与坐标轴平行的小六面体上 的应力来表示。共9个应力分量,三个正应 力,六个剪应力(如图2-1所示)
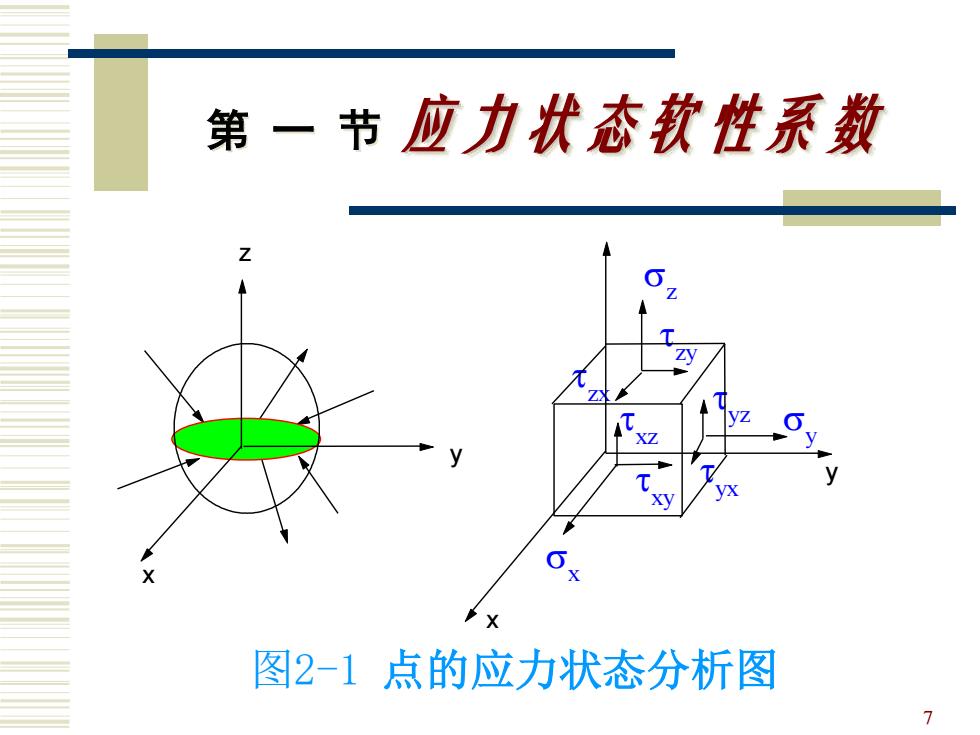
第一节应力状态软性系数 图2-1点的应力状态分析图 7
7 第 一 节 应力状态软性系数 0 2 图2-41 点的应力状态分析图 6 8 10 0 2 4 6 8 10 yx yz y xz xy x zx zy z z y x z y x X Title Y Title ###

第一节应力状态软性系数 Ox,oy,o:一三个正应力,垂直于截面; Tx,x,t,Tx, 六个切应力, 平行于截面,产生塑性变形。 由绕z轴的力距计算: (t·A正·Ay)Ax=(tx·Ax·△)A 可得:t=tyT)=TxTx=Tx 8
8 第 一 节 应力状态软性系数 ——三个正应力,垂直于截面; ——六个切应力, 平行于截面,产生塑性变形。 由绕z轴的力距计算: 可得: x y z , , xy xz yx yz z x z y , , , , , z y x x z y ( xy ) = ( yx ) xy yx = yz zy = xz zx =

第一节应力状态软性系数 上述计算结果表明,点的应力状态只要6 个应力分量就可以描述了。有6个应力分量 就对应有6个应变分量,三个正应变,三个 切应变。 Ox,Oy,0一正应力;Tw,tx,t一切应力: £x,Ey,8:一正应变;Y,Yx,Y一切应变: 9
9 第 一 节 应力状态软性系数 上述计算结果表明,点的应力状态只要6 个应力分量就可以描述了。有6个应力分量 就对应有6个应变分量,三个正应变,三个 切应变。 x y z , , xy xz yz , , x y z , , xy xz yz , , —正应力; —切应力; —正应变; —切应变;

第一节应力状态软性系数 二、三向应力状态下应力一应变 的关系(广义虎克定律) 单向应力状态的虎克定律:。 o-ES 在三向应力状态下,Ox除了在x方向产 生应变外,还在y,z方向产生横向收缩应 】 变,6y=82=-VEx=-V x E (负号表示收缩,V为泊松比) 10
10 第 一 节 应力状态软性系数 二、三向应力状态下应力-应变 的关系(广义虎克定律) 单向应力状态的虎克定律: G E = = x x E x y z x = = − = − 在三向应力状态下, 除了在 x 方向产 生应变 外,还在y, z方向产生横向收缩应 变, (负号表示收缩, 为泊松比)