
第六章扩散 第一节引言 第二节固体扩散机制及扩散动力学方程 第三节扩散系数 第四节影响扩散系数的因素
第六章 扩 散 第一节 引 言 第二节 固体扩散机制及扩散动力学方程 第三节 扩散系数 第四节 影响扩散系数的因素

扩散是物质内质点运动的基本方式,任何物系内的质点 都在做热运动。 ·扩散:当物质内有梯度(化学位、浓度、应力梯度等) 存在时,由于热运动而导致的质点定向迁移。 在气体和液体中,物质的传递方式除扩散外还可以通过 对流等方式进行;在固体中,扩散往往是物质传递的唯 一方式
扩散是物质内质点运动的基本方式,任何物系内的质点 都在做热运动。 ⚫ 扩散:当物质内有梯度(化学位、浓度、应力梯度等) 存在时,由于热运动而导致的质点定向迁移。 在气体和液体中,物质的传递方式除扩散外还可以通过 对流等方式进行;在固体中,扩散往往是物质传递的唯 一方式

扩散现象:大气污染、液体渗漏、半导体掺杂等现象, 就是有梯度存在情况下,气体在气体介质、液体在固 体介质中以及气体(或固体)在固体介质中的定向迁 移即扩散过程。 ·固体中发生的许多变化过程都与扩散密切相关:金 属的真空熔炼、金属高温蠕变以及金属的腐蚀、氧化; 无机非金属材料的制备与强化;高分子材料的加工与 改性
扩散现象:大气污染、液体渗漏、半导体掺杂等现象, 就是有梯度存在情况下,气体在气体介质、液体在固 体介质中以及气体(或固体)在固体介质中的定向迁 移即扩散过程。 ⚫ 固体中发生的许多变化过程都与扩散密切相关:金 属的真空熔炼、金属高温蠕变以及金属的腐蚀、氧化; 无机非金属材料的制备与强化;高分子材料的加工与 改性

固体中原子(或离子)的运动有两种不同的方式: >一种为大量原子集体的协同运动,或称机械运动; >一种为无规则的热运动,其中包括热振动和跳跃迁移。 所谓扩散是由于大量原子的热运动引起的物质的宏观迁 移
固体中原子(或离子)的运动有两种不同的方式: ➢ 一种为大量原子集体的协同运动,或称机械运动; ➢ 一种为无规则的热运动,其中包括热振动和跳跃迁移。 所谓扩散是由于大量原子的热运动引起的物质的宏观迁 移

一、从不同的角度对扩散进行分类 (1)按浓度均匀程度分: 有浓度差的空间扩散叫互扩散;没有浓度差的扩散叫自 扩散。 (2)按扩散方向分: 顺扩散:由高浓度区向低浓度区的扩散(下坡扩散); 逆扩散:由低浓度区向高浓度区的扩散(上坡扩散)
一、从不同的角度对扩散进行分类 (1)按浓度均匀程度分: 有浓度差的空间扩散叫互扩散;没有浓度差的扩散叫自 扩散。 (2) 按扩散方向分: 顺扩散:由高浓度区向低浓度区的扩散(下坡扩散); 逆扩散:由低浓度区向高浓度区的扩散(上坡扩散)

(3)按原子的扩散方向分: ●体扩散:在晶粒内部进行的扩散; ·表面扩散:在表面进行的扩散称为; ·晶界扩散:沿晶界进行的扩散称为。 表面扩散和晶界扩散的扩散速度比体扩散要快得多, 一般称前两种情况为短路扩散。此外还有沿位错线的 扩散,沿层错面的扩散等
(3) 按原子的扩散方向分: ⚫ 体扩散:在晶粒内部进行的扩散; ⚫ 表面扩散:在表面进行的扩散称为; ⚫ 晶界扩散:沿晶界进行的扩散称为。 表面扩散和晶界扩散的扩散速度比体扩散要快得多, 一般称前两种情况为短路扩散。此外还有沿位错线的 扩散,沿层错面的扩散等

二、扩散的推动力 当不存在外场时,晶体中粒子的迁移完全是由于热振动 引起的。只有在外场作用下,这种粒子的迁移才能形成 定向的扩散流。也就是说,形成定向扩散流必需要有推 动力,这种推动力通常是由浓度梯度提供的。 在普遍情况下,扩散推动力应是系统的化学位梯度;
二、扩散的推动力 当不存在外场时,晶体中粒子的迁移完全是由于热振动 引起的。只有在外场作用下,这种粒子的迁移才能形成 定向的扩散流。也就是说,形成定向扩散流必需要有推 动力,这种推动力通常是由浓度梯度提供的。 在普遍情况下,扩散推动力应是系统的化学位梯度;
7.1扩散动力学方程一菲克定律 7.1.1菲克第一定律 菲克参照傅里叶建立的导热方程,得出描述物质从高浓度区向 低浓度去迁移的定量公式。 假设有一单相固溶体,横截面积为A,浓度C不均匀。 C=C2 C:>C C=C 原始状态 最终状态 经扩散后 C 距离x一 图7.1扩散过程中溶质原子的分布
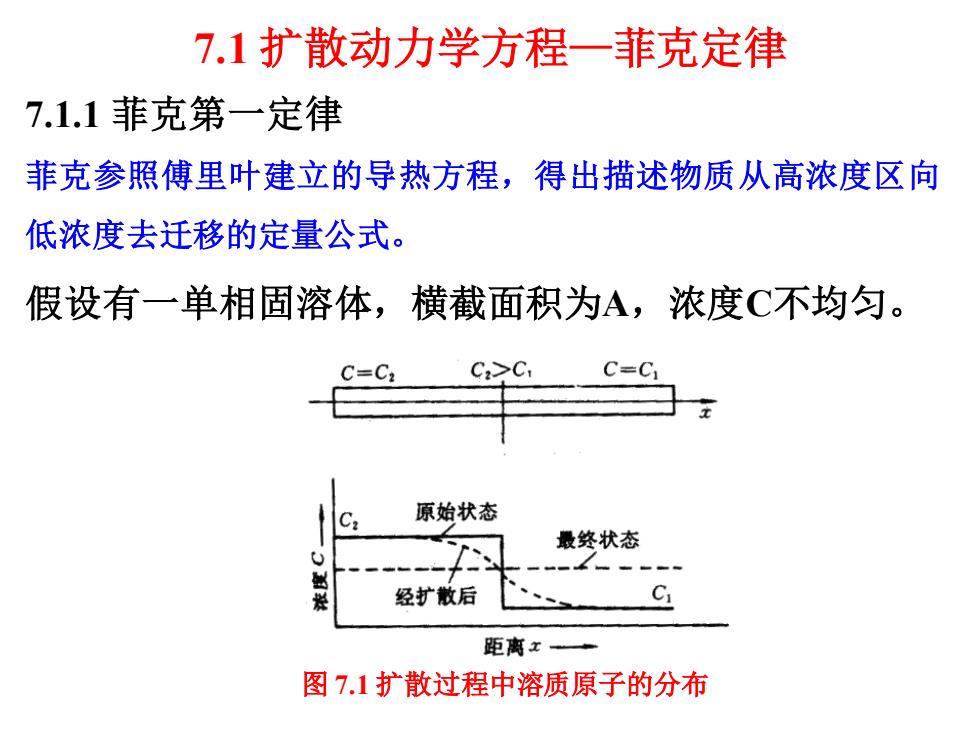
7.1 扩散动力学方程—菲克定律 7.1.1 菲克第一定律 菲克参照傅里叶建立的导热方程,得出描述物质从高浓度区向 低浓度去迁移的定量公式。 假设有一单相固溶体,横截面积为A,浓度C不均匀。 图 7.1 扩散过程中溶质原子的分布

在△时间内,沿x轴方向通过x处截面所迁移的物质 的量△m与处x的浓度梯度会C成正比: △C △mc A△t △X =-S
在△ t时间内,沿 x 轴方向通过 x 处截面所迁移的物质 的量△m 与处 x 的浓度梯度 成正比: A t x C m ( ) x C D Adt dm = −

7.1.2菲克第二定律 当扩散处于非稳态,即各点的浓度随时间而改变时, 利用式(7.1)不容易求出C(x,)。但通常的扩散过 程大都是非稳态扩散,为便于求出,还要从物质的 平衡关系着手,建立第二个微分方程式
7.1.2 菲克第二定律 当扩散处于非稳态,即各点的浓度随时间而改变时, 利用式(7.1)不容易求出C (x, t)。但通常的扩散过 程大都是非稳态扩散,为便于求出,还要从物质的 平衡关系着手,建立第二个微分方程式