《工程经济学》课程授课教案（土木工程专业）第五章 风险与不确定性分析

“工程经济学”教案 第五章不确定性分析 在前面介绍第四章内容时，我们有一个重要的假设前提，即不存在不确定因素，方案评 价时能得到完全信息。但是，未来实际发生的情况与事先的估算、预测很可能有相当大的出 入。为了提高经济评价的准确度和可信度，尽量避免和减少投资决策的失误，有必要对投资 方案做不确定性分析，为投资决策提供客观、科学的依据 ※本章要求 (1)了解不确定性分析的目的和意义： (2)掌握盈亏平衡分析方法： (3)掌握敏感性分析方法和步骤 (4)熟悉概率分析方法。 ※本幸重点 (1)线性盈亏平衡分析 (2)互斥方案的盈亏平衡分析 (3)单因素敏感性分析 (4)概率分析方法 ※本章唯点 (1)敏感性分析 (2)概率分析 §1盈亏平衡分析 一、独立方案的盈亏平衡分析 (一)线性盈亏平衡分析 设：Q0一年设计生产能力，Q一年产量或销量，P一单位产品售价，下一年固定成木 一单位变动成本 t一单位产品销售税金 则，可建立以下方程： 总收入方程：TR=P·2 年销传收入线 盈利区 总成本支出方程：TC=F+V:Q+tQ 年总成木线 故，利润方程为：B=TR-TC=(P-V-)Q-F 一周定成本找 令B=0,解出的Q即为BEP(Q)。 BEP(Q)=- BEP(Q 0 产量 P-V 进而解出生产能力利用率的盈亏平衡点BEP: 线性盈亏平衡分析图

“工程经济学”教案 1 收 入 、 费 用 BE BEP(Q Q 产量 亏损区 盈利区 年销售收入线 年总成本线 线性盈亏平衡分析图 固定成本线 第五章 不确定性分析 在前面介绍第四章内容时，我们有一个重要的假设前提，即不存在不确定因素，方案评 价时能得到完全信息。但是，未来实际发生的情况与事先的估算、预测很可能有相当大的出 入。为了提高经济评价的准确度和可信度，尽量避免和减少投资决策的失误，有必要对投资 方案做不确定性分析，为投资决策提供客观、科学的依据。 ※ 本章要求 （1）了解不确定性分析的目的和意义； （2）掌握盈亏平衡分析方法； （3）掌握敏感性分析方法和步骤； （4）熟悉概率分析方法。 ※ 本章重点 （1）线性盈亏平衡分析 （2）互斥方案的盈亏平衡分析 （3）单因素敏感性分析 （4）概率分析方法 ※ 本章难点 （1）敏感性分析 （2）概率分析 §1 盈亏平衡分析 一、独立方案的盈亏平衡分析 （一）线性盈亏平衡分析 设：Q0—年设计生产能力，Q—年产量或销量，P—单位产品售价，F—年固定成本， V—单位变动成本， t—单位产品销售税金 则，可建立以下方程： 总收入方程：TR = P ×Q 总成本支出方程：TC = F +V ×Q + t ×Q 故，利润方程为： B = TR -TC = (P -V - t)×Q - F 令 B＝0，解出的 Q 即为 BEP(Q)。 P V t F BEP Q - - ( ) = 进而解出生产能力利用率的盈亏平衡点 BEP(f)：

“工程经济学”教案 BEP(f)=BEP(Q)/Qox 100% 经营安全*：BEP(S)=1-BEP(Q 注意： 平衡点的生产能力利用率一般不应大于75%：经营安全率一般不应小于25%， 同理，还可求出其他因素的BEP。如达到设计生产能力时，产品销售价格的盈亏平衡 点为：BEP(P)= 【例】：教材P.95的例51或随机举例说明 (二)非线性盈亏平衡分析 在不完全竞争的条件下，销售收入和成本与产（销）量间可能是非线性的关系。非线性 盈亏平衡分析的原理同线性盈亏平衡分析，下面通过两道例题加以说明： 【例】：教材P.95的例52（销售收入是非线性，成本为线性的情况） 【例】：教材P96的例5-3（销售收入是非线性，成本也为非线性的情况 二、互斥方案的盈亏平衡分析 如有某个共同的不确定性因素影响互斥方案的取舍时，可先求出两两方案的盈亏平衡点 (BEP),再根据BEP讲行取金， 【例】：（寿命期为共同的不确定性因素）某产品有两种生产方案，方案A初始投资为 70万元，预期年净收益15万元：方案B初始投资170万元，预期年收益35万元。该项目 产品的市场寿命具有较大的不确定性，如果给定基准折现*为15%，不考虑期末资产残值， 试就项目寿命期分析两方案的临界点。 解：设项目寿命期为n NPV= -70+15(P1A,5%,n) PV=-170+35(PA,5%,n) 当NPVa=NPe时，有 -70+15(PIA,5%,n)=-170+35(P1A,5%,n) (PA,5%,n)=5 查复利系数表得n≈10年。 方案B 方案A 10 盈亏平衡图 这就是以项目寿命期为共有变量时方案A与方案B的盈亏平衡点。由于方案B年净收 益比较高，项目寿命期延长对方案B有利。故可知：如果根据市场预测项目寿命期小于10 年，应采用方案A;如果寿命期在10年以上，则应采用方案B

“工程经济学”教案 2 BEP(f)＝BEP(Q)/ Q0×100% 经营安全率：BEP(S)＝1－BEP(Q) 注意：平衡点的生产能力利用率一般不应大于 75%；经营安全率一般不应小于 25%。 同理，还可求出其他因素的 BEP。如达到设计生产能力时，产品销售价格的盈亏平衡 点为： V t Q F BEP P = + + 0 ( ) 【例】：教材 P.95 的例 5-1 或随机举例说明 （二）非线性盈亏平衡分析 在不完全竞争的条件下，销售收入和成本与产（销）量间可能是非线性的关系。非线性 盈亏平衡分析的原理同线性盈亏平衡分析，下面通过两道例题加以说明： 【例】：教材 P.95 的例 5-2（销售收入是非线性，成本为线性的情况） 【例】：教材 P.96 的例 5-3（销售收入是非线性，成本也为非线性的情况） 二、互斥方案的盈亏平衡分析 如有某个共同的不确定性因素影响互斥方案的取舍时，可先求出两两方案的盈亏平衡点 （BEP），再根据 BEP 进行取舍。 【例】：（寿命期为共同的不确定性因素）某产品有两种生产方案，方案 A 初始投资为 70 万元，预期年净收益 15 万元；方案 B 初始投资 170 万元，预期年收益 35 万元。该项目 产品的市场寿命具有较大的不确定性，如果给定基准折现率为 15%，不考虑期末资产残值， 试就项目寿命期分析两方案的临界点。 解：设项目寿命期为 n NPVA＝－70＋15（P/A，5%，n） NPVB＝－170＋35（P/A，5%，n） 当 NPVA＝NPVB时，有 －70＋15（P/A，5%，n）＝－170＋35（P/A，5%，n） （P/A，5%，n）＝5 查复利系数表得 n≈10 年。 这就是以项目寿命期为共有变量时方案 A 与方案 B 的盈亏平衡点。由于方案 B 年净收 益比较高，项目寿命期延长对方案 B 有利。故可知：如果根据市场预测项目寿命期小于 10 年，应采用方案 A; 如果寿命期在 10 年以上，则应采用方案 B。 NPV 方案 A n 方案 B N=10 盈亏平衡图

“工程经济学”教案 【例】：教材P.97的例55（产量为共同的不确定性因素） §2敏感性分析 一、概述 1.含义 2.主要任务 二、单因素敏感性分析 假设某一不确定性因素变化时，其他因素不变，即各因素之间是相互独立的。下面通过 例题来说明单因素敏感性分析的具体操作步 (1)确定研究对象（选最有代表性的经济效果评价指标，如IRR、NPV) (2)选取不确定性因素（关键因素，如R、C、K、n) (3)设定因素的变动范围和变动幅度（如一20%~+20%，10%变动） (4)计算某个因素变动时对经济效果评价指标的影响 ◆计算敏感度系数并对敏感因素进行排疗 敏感度系数的计算公式为： B=△AW△ 式中，B为评价指标A对于不确定因素F的敏感度系数： △A为不确定因素F发生△F变化率时，评价指标A的相应变化率(%)： △F为不确定因素F的变化率(%)。 ◆计算变动因素的临界点。临界点是指项目允许不确定因素向不利方向变化的极限值， 超过极限，项目的效益指标将不可行。 (5)绘制敏感性分析图，作出分析。 【例】：设某项目基本方案的基本数据估算值如下表所示，试就年销售收入B、年经营 成本C和建设投资1对内部收益率进行单因素敏感性分析（基准收益率1=8%）。 基本方案的基本数据估笪表 建设投资年销 年经成本 因素 万元 估算值 1500 600 200 解： (1)计算基本方案的内部益率RR -10+RR)-+(B-C+1RR)+(B+L-C+1RR)=0 -15001+RR'+3502+RR'+501+R=0 采用试算法得： WPVi=8%)=31.08(万元)>0， NPV0=9%)=-7.92(万元)<0 采用线性内插法可求得： IRR=8% 31.08+79299%-89%)=879% 31.08 (2)计算销售收入、经营成本和建设投资变化对内部收益率的影响，结果见下表。 3

“工程经济学”教案 3 【例】：教材 P.97 的例 5-5（产量为共同的不确定性因素） §2 敏感性分析 一、概述 1. 含义 2. 主要任务 二、单因素敏感性分析 假设某一不确定性因素变化时，其他因素不变，即各因素之间是相互独立的。下面通过 例题来说明单因素敏感性分析的具体操作步骤： （1）确定研究对象（选最有代表性的经济效果评价指标，如 IRR、NPV） （2）选取不确定性因素（关键因素，如 R、C、K、n） （3）设定因素的变动范围和变动幅度（如－20％～+20％，10％变动） （4）计算某个因素变动时对经济效果评价指标的影响 ◆计算敏感度系数并对敏感因素进行排序。敏感度系数的计算公式为： β=△A/△F 式中，β为评价指标 A 对于不确定因素 F 的敏感度系数； △A 为不确定因素 F 发生△F 变化率时，评价指标 A 的相应变化率（%）； △F 为不确定因素 F 的变化率（%）。 ◆计算变动因素的临界点。临界点是指项目允许不确定因素向不利方向变化的极限值。 超过极限，项目的效益指标将不可行。 （5）绘制敏感性分析图，作出分析。 【例】：设某项目基本方案的基本数据估算值如下表所示，试就年销售收入 B、年经营 成本 C 和建设投资 I 对内部收益率进行单因素敏感性分析（基准收益率 ic=8%）。 基本方案的基本数据估算表 因素 建设投资 I(万元) 年销售收入 B(万元) 年经营成本 C(万元) 期末残值 L(万元) 寿命 n(年) 估算值 1500 600 250 200 6 解：（1）计算基本方案的内部益率 IRR： å å = - - - = - - - - + + + + + = - + + - + + + - + = 5 2 1 6 5 2 1 6 1500(1 ) 350 (1 ) 550(1 ) 0 (1 ) ( ) (1 ) ( )(1 ) 0 t t t t IRR IRR IRR I IRR B C IRR B L C IRR 采用试算法得: NPV(i=8%)=31.08（万元）>0， NPV(i=9%)=－7.92（万元）<0 采用线性内插法可求得： (9% 8%) 8.79% 31.08 7.92 31.08 8% - = + IRR = + （2）计算销售收入、经营成本和建设投资变化对内部收益率的影响，结果见下表

“工程经济学”教案 因素变化对内部收益率的影响 内部收益率% 、变化泽 -10% -5% 基本方案 +5% +10% 不确定因素 销收 3.01 8.79 1158 1420 建设投资 12.7010.67 7.06 5.45 内部收益率的敏感性分析图见下图。 内部收益率(%) 年销售收 投资 基本方案(8.79%》 年经营成本 基准收益率8% 10% -5% *5% +10不确定性因素变化率 单因素敏感性分析图 (3)计算方案对各因素的敏感度 平均敏感度的计算公式如下： 评价指标变化的幅度(%) B不确定性因素变化的幅度阿 年销售收入平均敏感度=1430-301 0.56 20 年经营成本平均敏感度：62-11☑.024 20 建设投资平均度545-1206 20 三、多因素敏感性分析 1.最有利一最不利法 【例1：教材P99的例57 2.解折法与作图法结合 【例1：教材P100的例5-8（二元变化，关键因素是初始投资和年收入） 【例】：教材P100的例5-8（三元变化，关键因素是初始投资、年收入和寿命） 说明：敏感性分析的优缺点：Exc©软件在敏感性分析中的应用

“工程经济学”教案 4 因素变化对内部收益率的影响 内部收益率% 变化率 不确定因素 -10% -5% 基本方案 +5% +10% 销售收入 3.01 5.94 8.79 11.58 14.30 经营成本 11.12 9.96 8.79 7.61 6.42 建设投资 12.70 10.67 8.79 7.06 5.45 内部收益率的敏感性分析图见下图。 －10% －5% 0 +5% +10% 单因素敏感性分析图 （3）计算方案对各因素的敏感度 平均敏感度的计算公式如下： ( ) (%) % 不确定性因素变化的幅度 评价指标变化的幅度 b = 年销售收入平均敏感度= 0.56 20 14.30 3.01 = - 年经营成本平均敏感度= 0.24 20 6.42 11.12 = - 建设投资平均敏感度= 0.36 20 5.45 12.70 = - 三、多因素敏感性分析 1. 最有利—最不利法 【例】：教材 P.99 的例 5-7 2. 解析法与作图法结合 【例】：教材 P.100 的例 5-8（二元变化，关键因素是初始投资和年收入） 【例】：教材 P.100 的例 5-8（三元变化，关键因素是初始投资、年收入和寿命） 说明：敏感性分析的优缺点；Excel 软件在敏感性分析中的应用。 年销售收入 年经营成本 基本方案（8.79%） 投资 基准收益率(8%） 内部收益率(%) 不确定性因素变化率

“工程经济学”教案 §3概率分析 一、随机参数的概率分布 1.均匀分布 均值：X)]=a+b 。a为参数取值的最小值 2 方差：D]=6-a b为参数取值的最大值 12 2.B分布 对参数作出三种估计值：悲观值P、最可能值M、乐观值O 均值：EX灯=P+4M+O 6 方mm-o: 3.正态分布 X~N(4,G2,EX刈=4， DX☒=o2 二、解析法（以净现值作为分析的主要指标） 1.净现值的期望与方差 设各年的净现金流量为独立同分布随机变量工（化=0,1,2，），则 NPr=2+)厂 则：ENPV)=∑Ey,)-1+1,) 「E(kE)=kE(E)] D(NPV)-()( 【:Dk5)片=K2D(5)] σ(NPV)=√DNP(（净现值的方差与净现值是不同的量纲，“用标准差) 由中心极限定理，当n很大时，NPV~N(E(NPV),DNPV) 作标准化处理： NPV -E(NPV)-N(0,1) G(NPV) 【例1：教材P104的例5-9 2.方案的风险分析

“工程经济学”教案 5 §3 概率分析 一、随机参数的概率分布 1. 均匀分布 均值： 2 [ ] a b E X + = a 为参数取值的最小值 方差： 12 ( ) [ ] 2 b a D X - = b 为参数取值的最大值 2. β分布 对参数作出三种估计值：悲观值 P、最可能值 M、乐观值 O 均值： 6 4 [ ] P M O E X + + = 方差： 2 6 [ ] ÷ ø ö ç è æ - = O P D X 3. 正态分布 2 2 X ~ N(m,s ), E[X] = m, D[X] = s 二、解析法（以净现值作为分析的主要指标） 1. 净现值的期望与方差 设各年的净现金流量为独立同分布随机变量Y (t 0,1,2, , n) t = L ，则 å= - = + n t t t c NPV Y i 0 (1 ) 则： å= - = × + n t t t c E NPV E Y i 0 ( ) ( ) (1 ) [∵E(kξ)=kE(ξ)] å= - = × + n t t t c D NPV D Y i 0 2 ( ) ( ) (1 ) [∵D(kξ)=k2D(ξ)] s (NPV ) = D(NPV ) (∵净现值的方差与净现值是不同的量纲，∴用标准差) 由中心极限定理，当 n 很大时， NPV ~ N(E(NPV ), D(NPV )) 作标准化处理： ~ (0, 1) ( ) ( ) N NPV NPV E NPV s - 【例】：教材 P.104 的例 5-9 2. 方案的风险分析

“工程经济学”教案 【例1：教材P.105的例5-10 NPrN01739.9433,亦即Pr-1739、N0,) 9.433 （1 PANPV≥0)=1-PNpr<0y=1-0-11739)=1-1+124=0.8925 9.433 【例1：教材P106的例5-11 三、概率树分析 概幸树分析的一般步骤是： (1)列出要考虑的各种风险因素，如投资、经营成本、销售价格等： (2)设想各种风险因素可能发生的状态，即确定其数值发生变化个数： (3)分别确定各种状态可能出现的概率，并使可能发生状态概率之和等于1： (4)分别求出各种风险因素发生变化时，方案净现金流量各状态发生的概率和相应状态下 的净现值NPm: (5)求方案净现值的期望值（均值）E(NPV): 式中P为第种状态出现的概率 k为可能出现的状态数 (6)求出方案净现值非负的累计概率： (7)对概率分析结果作说明。 【例】：某商品住宅小区开发项目现金流量的估计值如下表1所示 根据经验推断新，销 售收入和开发成本为离散型随机变量，其值在估计值的基础上可能发生的变化及其概率见 表2。试确定该项目净现值大于等于零的概率。基准收益率=12%。 表1 基本方案的参数估计 单位：万元 年份 销售收入 857 7143 8800 开发成本 48 其他税费 净现金流量 -5087 1806 9350 表2 不确定性因素的变化范用 20% 0 +20% 收本 86 解：(1)项日净现金流量未来可能发生的9种状态如下图。 (2)分别计算项目净现金流量各种状态的概率1,2，9) P,=0.2X0.6=0.1 P2=0.2×0.3=0.06 P3=0.2×0.1=0.02 余类推。结果见下图。 (3)分别计算项目各状态下的净现值NPV(=1,2,9)》

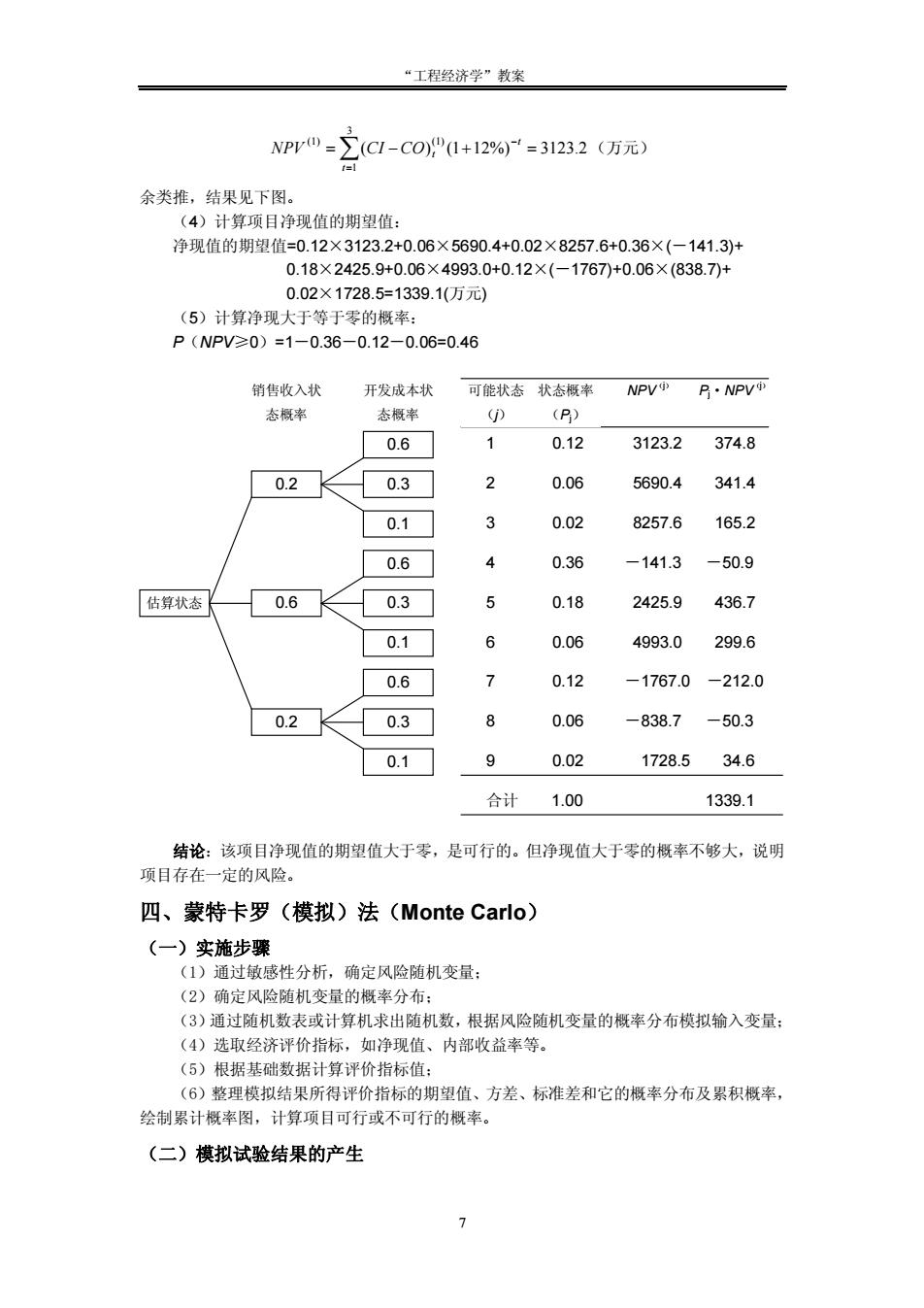
“工程经济学”教案 6 【例】：教材 P.105 的例 5-10 ~ (11.739, 9.433 ) 2 NPV N ，亦即 ~ (0, 1) 9.433 11.739 N NPV - （1） ) 1 1 (1.24) 0.8925 9.433 0 11.739 ( 0) 1 ( 0) 1 ( = - + F = - P NPV ³ = - P NPV < = - F 【例】：教材 P.106 的例 5-11 三、概率树分析 概率树分析的一般步骤是: （1）列出要考虑的各种风险因素，如投资、经营成本、销售价格等； （2）设想各种风险因素可能发生的状态，即确定其数值发生变化个数； （3）分别确定各种状态可能出现的概率，并使可能发生状态概率之和等于 1； （4）分别求出各种风险因素发生变化时，方案净现金流量各状态发生的概率和相应状态下 的净现值 NPV(j)； （5）求方案净现值的期望值（均值）E（NPV）； . ( ) k 1 (j) 为可能出现的状态数 式中 为第 种状态出现的概率 k P j E NPV NPV P j j å j = = ´ （6）求出方案净现值非负的累计概率； （7）对概率分析结果作说明。 【例】：某商品住宅小区开发项目现金流量的估计值如下表 1 所示，根据经验推断，销 售收入和开发成本为离散型随机变量，其值在估计值的基础上可能发生的变化及其概率见下 表 2。试确定该项目净现值大于等于零的概率。基准收益率 ic=12%。 表 1 基本方案的参数估计 单位：万元 年份 1 2 3 销售收入 开发成本 其他税费 857 5888 56 7143 4873 464 8800 6900 1196 净现金流量 -5087 1806 9350 表 2 不确定性因素的变化范围 变幅 概率 因素 －20% 0 +20% 销售收入 开发成本 0.2 0.1 0.6 0.3 0.2 0.6 解：（1）项目净现金流量未来可能发生的 9 种状态如下图。 （2）分别计算项目净现金流量各种状态的概率 Pj（j=1，2，.，9）： P1=0.2×0.6=0.12 P2=0.2×0.3=0.06 P3=0.2×0.1=0.02 余类推。结果见下图。 （3）分别计算项目各状态下的净现值 NPVj（j=1，2，.，9）

“工程经济学”教案 NP0=.(C1-C0"(1+12%=3123.2(万元) 余类推，结果见下图 (4)计算项目净现值的期望值： 净现值的期望值=0.12×3123.2+0.06×5690.4+0.02×8257.6+0.36×(-141.3)+ 0.18×2425.9+0.06×4993.0+0.12×(-1767+0.06×(838.7)+ 0.02×1728.5=1339.1(万元) (5)计算净现大于等于零的概率： P(NPV≥0)=1-0.36-0.12-0.06=0.46 销售收入状 开发成本状 可能状态状态概率 NPV P·NPVT 态概率 态概率 ( (B) 0.6 1 0.12 3123.2 374.8 0.2 0.3 2 0.06 5690.4 341.4 0.1 3 0.02 8257.6 165.2 0.6 4 0.36 -141.3 -50.9 估算状态 0.6 0.3 5 0.18 2425.9 436.7 0.1 6 0.06 4993.0 299.6 0.6 7 0.12 -1767.0 -212.0 0.2 0.3 0.06 -838.7 -50.3 0.1 9 0.02 1728.534.6 合计1.00 1339.1 结论：该项目净现值的期望值大于零，是可行的。但净现值大于零的概率不够大，说明 项目存在一定的风险。 四、蒙特卡罗（模拟）法(Monte Carlo) (一)实施步骤 (1)通过敏感性分析，确定风险随机变量 (2)确定风险随机变量的概率分布： (3)通过随机数表或计算机求出随机数，根据风险随机变量的概率分布模拟输入变量： (4)选取经济评价指标，如净现值、内部收益率等。 (5)根据基础数据计算评价指标值： (6)整理模拟结果所得评价指标的期望值、方差、标准差和它的概率分布及累积概率 绘制累计概率图，计算项目可行或不可行的概率。 (二)模拟试验结果的产生 >

“工程经济学”教案 7 å= - = - + = 3 1 (1) (1) ( ) (1 12%) 3123.2 t t NPV CI CO t （万元） 余类推，结果见下图。 （4）计算项目净现值的期望值： 净现值的期望值=0.12×3123.2+0.06×5690.4+0.02×8257.6+0.36×(－141.3)+ 0.18×2425.9+0.06×4993.0+0.12×(－1767)+0.06×(838.7)+ 0.02×1728.5=1339.1(万元) （5）计算净现大于等于零的概率： P（NPV≥0）=1－0.36－0.12－0.06=0.46 结论：该项目净现值的期望值大于零，是可行的。但净现值大于零的概率不够大，说明 项目存在一定的风险。 四、蒙特卡罗（模拟）法（Monte Carlo） （一）实施步骤 （1）通过敏感性分析，确定风险随机变量； （2）确定风险随机变量的概率分布； （3）通过随机数表或计算机求出随机数，根据风险随机变量的概率分布模拟输入变量； （4）选取经济评价指标，如净现值、内部收益率等。 （5）根据基础数据计算评价指标值； （6）整理模拟结果所得评价指标的期望值、方差、标准差和它的概率分布及累积概率， 绘制累计概率图，计算项目可行或不可行的概率。 （二）模拟试验结果的产生 估算状态 0.2 0.6 0.6 0.3 0.1 0.6 0.3 0.1 0.6 0.3 0.1 0.2 销售收入状 态概率 开发成本状 态概率 可能状态 （j） 状态概率 （Pj） NPV（j） Pj·NPV（j） 1 0.12 3123.2 374.8 2 0.06 5690.4 341.4 3 0.02 8257.6 165.2 4 0.36 －141.3 －50.9 5 0.18 2425.9 436.7 6 0.06 4993.0 299.6 7 0.12 －1767.0 －212.0 8 0.06 －838.7 －50.3 9 0.02 1728.5 34.6 合计 1.00 1339.1

“工程经济学”教案 1.离散型：用教材P107的例5-11或随机举例加以说明 2.连续型 (1)正态分布试验结果的产生 随机数(RN)作为随机变量累积概率的随机值，这样，每个随机数都可找到对应的一 个随机正态偏差(RND 试验结果=均值+随机正态偏差×标准差 【例】：教材P108或随机举例 (2)均匀分布试验结果的产生 随机数(RN)作为随机变量累积概率的随机值，设RNm一最大随机数 试验结果=a+ 6-a)=a+_6-a RN RN(b-a) 22'RN 【例】：随机举例 (三)非独立随机变量的模拟 【例】：教材P.109的例5-12 ◆年净现金流量(y)服从正态分布： EX)=10000元，a()=2000元→试验结果=10000+RND×2000 ◆寿命()服从均匀分布，且均值是净现金流量的函数： EX)=0.0005y,D-a)=6→实验结果=0.0005y-3+(RNRN)×6 (四)独立随机变量的模拟 【例】：教材P.109的例5-13 ◆寿命服从均匀分布： a=12,b=16→实验结果=12+(RN/RNm))×4 ◆年净现金流量服从正态分布： EX)=25万元，o(X)=3万元→试验结果=25+RNDX3 说明：概率分析的软件很多，这里仅介绍Risk4.0软件（可从www.paIisade.com 网上下载)，它是使用Excel的工作页，用Monte Carlo模拟来进行计算的

“工程经济学”教案 8 1. 离散型：用教材 P.107 的例 5-11 或随机举例加以说明 2. 连续型 （1）正态分布试验结果的产生 随机数（RN）作为随机变量累积概率的随机值，这样，每个随机数都可找到对应的一 个随机正态偏差（RND）。 试验结果＝均值+随机正态偏差×标准差 【例】：教材 P.108 或随机举例 （2）均匀分布试验结果的产生 随机数（RN）作为随机变量累积概率的随机值，设 RNm—最大随机数 ( ) 2 2 ( ) b a RN a b b a RN b a RN RN a m m + - - - + 试验结果＝ + - = 【例】：随机举例 （三）非独立随机变量的模拟 【例】：教材 P.109 的例 5-12 ◆ 年净现金流量（y）服从正态分布： E(X)=10000 元，σ(X)=2000 元 试验结果＝10000+RND×2000 ◆ 寿命（n）服从均匀分布，且均值是净现金流量的函数： E(X)=0.0005y，(b-a)=6 实验结果＝0.0005y－3+(RN/RNm)×6 （四）独立随机变量的模拟 【例】：教材 P.109 的例 5-13 ◆ 寿命服从均匀分布： a=12，b=16 实验结果＝12+(RN/RNm)×4 ◆ 年净现金流量服从正态分布： E(X)=25 万元，σ(X)=3 万元 试验结果＝25+RND×3 说明：概率分析的软件很多，这里仅介绍 Risk4.0 软件（可从www.palisade.com 网上下载），它是使用 Excel 的工作页，用 Monte Carlo 模拟来进行计算的