
试卷代号:1024 座位号■■ 中央广播电视大学2007一2008学年度第一学期“开放本科”期末考试 计算机专业 信号处理原理试题 2008年1月 题 号 二 三 四 五 六 总 分 分 数 得 分 评卷人 一、判断题(每小题3分,共15分) Sa(t)dt =1 2.函数f(t)与单位冲激函数的卷积是f(t)米6(t一to)=f(t一t6) 3.时不变系统的响应与激励施加的时刻是没有关系的。 4.Sa信号的傅立叶变换是奇函数。 5.序列x()不是因果序列,其Z变换为X(z),x(n)向右平移5个单位后再求取单边Z 变换,结果一定是Z孔x(n-5)]=xX(x)。 得 分 评卷人 二、单项选择题(每小题5分,共25分】 1.下面的描述不属于卷积性质的是()。 A.交换律 B.分配律 C.结合律 D.加法律 167
试卷代号 :1024 座位号巨口 中央广播电视大学2007-2008学年度第一学期“开放本科”期末考试 计算机专业 信号处理原理 试题 2008年 1月 题 号 四 五 尸、 总 分 分 数 得 分 评卷人 一、判断题(每小题 3分,共 15分 ) ‘·{}0sUct>at一‘ ( ) 2.函数 f(a)与单位冲激函数的卷积是 f } 8=f(t-t}> ( ) 3.时不变系统的响应与激励施加的时刻是没有关系的。 ( ) 4. S“信号的傅立叶变换是奇函数。 ( ) 5.序列x(n)不是因果序列,其 Z变换为 X(z),x(n)向右平移 5个单位后再求取单边 Z 变换,结果一定是Z[x (1:一5)]=z}X(z}。 得 分 评卷人 二、单项选择题(每小题 5分,共 25分 ) 1.下面的描述不属于卷积性质的是( A.交换律 B.分配律 C.结合律 D.加法律 167

2.下面关于信号分解的说法正确的是()。 A,信号可以分解为直流分量和交流分量 B.信号可以分解为确定分量与不确定分量 C.信号可以分解为模拟分量与数字分量 D.信号可以分解为连续分量与离散分量 3.偶周期性方波信号的傅立叶级数不可能有( )。 A.余弦项和直流项 B.正弦项 C.正弦项和直流项 D.余弦项 4,单位冲激信号的拉普拉斯变换结果是( )。 A.0 B.1 C.1/s D.-1 5.因果序列u(n)ZT的ROC是()。 A.右半平面 B.某个圆内区域 C.某个圆外区域 D.某个环形区域 得分 评卷人 三、填空题(每小题4分,共20分)】 Sa (t)8(t)dt= 2.指数信号的积分、微分是 3.傅里叶变换的线性特性,包含两部分: 和 4.单位阶跃序列的Z变换结果为: 5.离散傅立叶变换中的W×= 168
.下面关于信号分解的说法正确的是( A,信号可以分解为直流分量和交流分量 B.信号可以分解为确定分量 与不确定分量 C.信号可以分解为模拟分量与数字分量 D.信号可以分解为连续分量与离散分量 .偶周期性方波信号的傅立叶级数不可能有( A,余弦项和直流项 B、正弦项 C.正弦项和直流项 D.余弦项 单位冲激信号的拉普拉斯变换结果是( C. 1/s D_ 一 1 .因果序列 u(n) ZT的ROC是( A。右半平面 B,某个圆内区域 C.某个圆外区域 D.某个环形区域 得 分 评卷人 三、填空题 (每小题 4分,共 20分) l.{几Sci(t)8(t)dt- 指数信号的积分、微分是 傅里叶变换的线性特性 ,包含两部分 : 单位阶跃序列的2变换结果为: 离散傅立叶变换中的 W、 168

得分 评卷人 四、证明题(10分) 若牙[f(t)]=F(w,则孚[f(t-t。)]=F(w)e 得分 评卷人 五、计算题(每小题10分,共20分) 1.试求信号f(t)=eu(t)傅立叶变换的频谱函数F(w) 2.求序列x(n)=(2"+1)u(n)的ZT结果 得分 评卷人 六、作图题(10分)】 绘出f(t)=u(cost)在区间(一3π,3π)之间的波形。 169
得 分 评卷人 四、证明题 (10分) 若}"一C.ftt)}'-F(w>,则 .}[f(t一to)〕“F(cu)e 得 分 评卷人 五、计算题(每小题 10分。共 20分) 1.试求信号 f(t)=e Z`u(t)傅立叶变换的频谱函数 F(cu) 2.求序列 x(n)=(2}"-}-1)u(n) 的 ZT结果 得 分 评卷人 六、作图题 (10分 ) 绘出 f(t) = u(cost)在区间(-3n, 3}r)之间的波形 。 169

试卷代号:1024 中央广播电视大学2007一2008学年度第一学期“开放本科”期末考试 计算机专业 信号处理原理试题答案及评分标准 (供参考) 2008年1月 一、判断题(每小题3分,共15分) 1.错误 2.正确 3.正确 4.错误 5.错误 二、单项选择题(每小题5分,共25分】 1.D 2.A 3.B 4.B 5.C 三、填空题(每小题4分,共20分)】 1.1 2.指数信号 3.齐次性 叠加性 4产 5.e将 四、证明题(10分)】 证明: 因为 [ft-o)】=ft-6)e=d (3分) 170
试卷代号:1024 中央广播电视大学2007-2008学年度第一学期“开放本科”期末考试 计算机专业 信号处理原理 试题答案及评分标准 (供参考) 2008年 1月 一、判断题 (每小题 3分 ,共 15分) 1.错误 2.正确 3.正确 4.错误 5.错 误 二、单项选择题(每小题 5分,共 25分 ) l. D 2. A 3. B 4. B 5. C 三、填空题 (每小题 4分 ,共 20分) l. 1 2.指数信号 3.齐次性 叠加性 ’2 、一 1 5.e-jv 四、证明题(10分) 证 明 : 因为 170 少巨f(t一t,)二= f(c一t)e-iw} cjt (3分) 尸I 丫 U
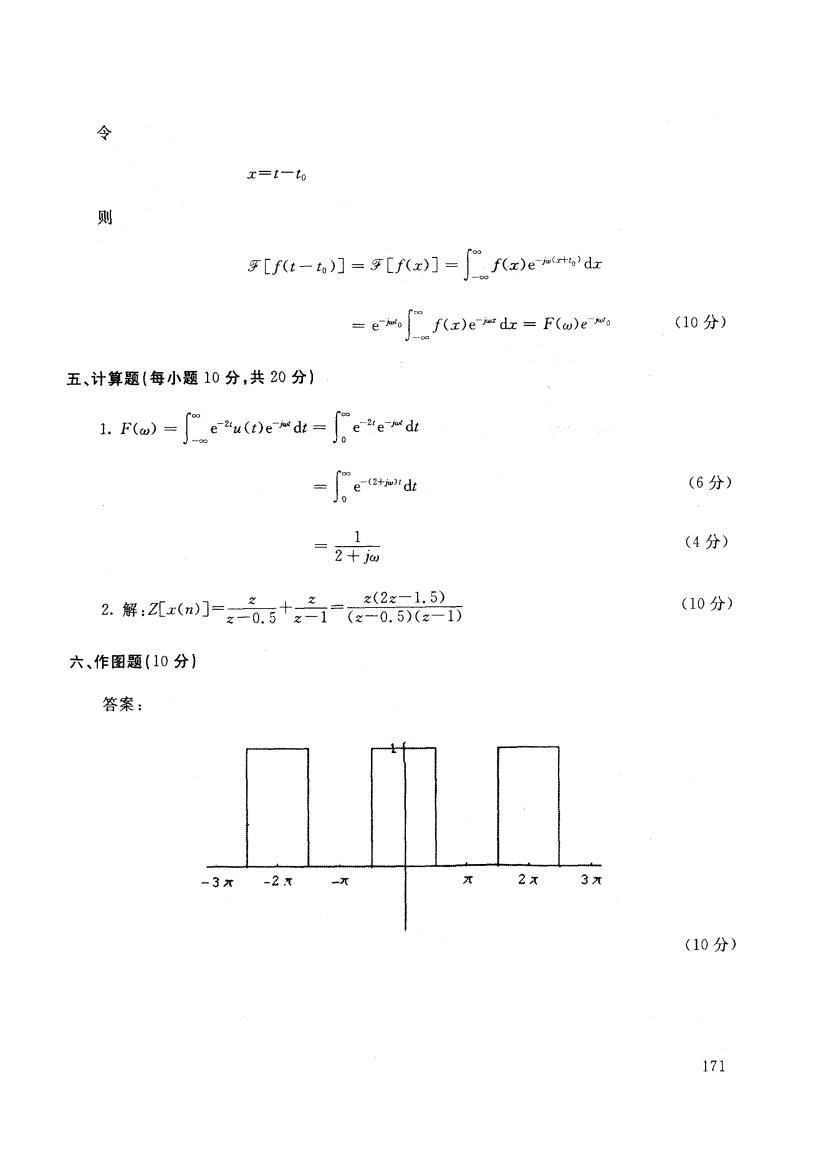
令 x=t-to 则 [f(t-1)]=9[f(z)]=f(a)emm d =efxe加d=Foe (10分) 五、计算题(每小题10分,共20分) 1.ra)=cu(0ed=e"ed de (6分) 1 =2+jo (4分) z(2x-1.5) 2.解:x(m]=05十-8 (10分) 六、作图题(10分) 答案: -3x-2 2x 3元 (10分) 171
令 x= t一 to 则 、[f(t一to)J = }} [f(x)] _几f (x) e-'}'+`} dx -一{几f(x)一、一:(。)。一 (10分) 五、计算题 (每小题 10分 ,共 20分) 1. F(w)一f.一(:)一d,一!0一 dt {了一(z+;},> } dt (6分) 1 2+ 1w (4分) 2.解:Z[x(n)」特一 z + z一 U. 5 z z一 1 z(2z一1. 5) (z一0. 5)(z一 1) (10分) 六、作图题 (10分 ) 答案 : (10分) 171