
China-pub.com 下载 第11章 积分和微分方程组 在有效的MATLAB命令帮助下,可以求解出定积分和普通微分方程的数字解并绘制出其 图形。 11.1 积分 在MATLAB中能求解如下形式的定积分并给出数字解: g=g(x)dx 有许多方法都可以能够解决积分问题(又叫做求面积)。如果要用MATLAB监控整个计算 过程,可以使用guad命令。同样能计算出被积函数g的值,并且让MATLAB使用梯形规则和 trapz命令计算出积分。当只有离散的数据点和被积函数的数学表达式为未知时,这种方法 是非常有效的。 命令集107 定积分计算 trapz(x,y) 计算出函数的积分并将结果返回到。向量x和y有相同的长度, i,y代表曲线上的一点。曲线上点的距离不一定相等,x值也 不一定有序。然而,负值间距和子区间被认为是负值积分。 trapz(y) 计算方法同上,但x值间隔为1。 trapz(x,A) 将A中每列的值带入x的函数算出其积分,并返回一组包含 积分结果的向量。A的列向量必须和向量x的长度相同。 Z=trapz(x,A,dim) 在矩阵A中dim指定的维内进行数据积分。如果给定向量x, 则x的长度必须与size(A,dim)相同。 cumtrapz(A,dim) 返回大小和A相同的数组,包含的是将矩阵A进行梯形积分 的累积值。如果dim已给定,则在dim维内进行计算。 quad(fcn,a,b) 返回在区间a,b]上g的积分近似值。字符串fcn包含一个与g相 对应的MATLAB函数名,也就是预定义函数或者是M文件。 这个函数接收一个向量参数,并返回一个向量结果。 MATLAB利用辛普森规则执行递归的积分,计算误差为1O~。 guad(fcn,a,b,tol)求g的积分近似值,其相对误差由参数tol定义。否则,计算 过程同上。 quad(fcn,ab,tol求g的积分近似值,其相对误差由参数tol所定义。如果参数 pic) pic是非零值,则在图形中显示求值的点。 quad(···,trace) 如果trace是非零值,则画出积分图形
下载 第11章 积分和微分方程组 在有效的M AT L A B命令帮助下,可以求解出定积分和普通微分方程的数字解并绘制出其 图形。 11.1 积分 在M AT L A B中能求解如下形式的定积分并给出数字解: 有许多方法都可以能够解决积分问题 (又叫做求面积 )。如果要用 M AT L A B监控整个计算 过程,可以使用 q u a d命令。同样能计算出被积函数 g的值,并且让M AT L A B使用梯形规则和 t r a p z命令计算出积分。当只有离散的数据点和被积函数的数学表达式为未知时,这种方法 是非常有效的。 命令集1 0 7 定积分计算 t r a p z ( x , y ) 计算出函数x的积分并将结果返回到y。向量x和y有相同的长度, (xi, yi)代表曲线上的一点。曲线上点的距离不一定相等,x值也 不一定有序。然而,负值间距和子区间被认为是负值积分。 t r a p z ( y ) 计算方法同上,但x值间隔为1。 t r a p z ( x , A ) 将A中每列的值带入 x的函数算出其积分,并返回一组包含 积分结果的向量。A的列向量必须和向量x的长度相同。 Z = t r a p z ( x , A , d i m ) 在矩阵A中d i m指定的维内进行数据积分。如果给定向量 x, 则x的长度必须与size(A, dim)相同。 c u m t r a p z ( A , d i m ) 返回大小和A相同的数组,包含的是将矩阵 A进行梯形积分 的累积值。如果d i m已给定,则在d i m维内进行计算。 q u a d ( f c n , a , b ) 返回在区间[a, b]上g的积分近似值。字符串f c n包含一个与g相 对应的M AT L A B函数名,也就是预定义函数或者是 M文件。 这个函数接收一个向量参数,并返回一个向量结果。 M AT L A B利用辛普森规则执行递归的积分,计算误差为1 0-3。 q u a d ( f c n , a , b , t o l ) 求g的积分近似值,其相对误差由参数 t o l定义。否则,计算 过程同上。 quad(fcn,a b,tol,求g的积分近似值,其相对误差由参数 t o l所定义。如果参数 p i c ) p i c是非零值,则在图形中显示求值的点。 q u a d (. . ., t r a c e ) 如果t r a c e是非零值,则画出积分图形

152 China-pub.com MATLAB5手册 下载 guad8(···) 可以与quad一样用于相同的参数组合并返回相同的结果, 但使用更高精度的方法。因此,如果被积函数的导数在某一 区间内是不定的,例如:9=5md,使用此命令将会更好 一些。quad和quad8都要求被积函数在整个区间里是有限的。 dblquad(f,min1,计算双变量函数f的二重积分。函数中的第一个自变量用于 max1,min2,max2, 内层积分。内层积分在minl和nax 1之间进行,外层积分在 tol,trace,order) min2和max2之间进行。变量tol指定相对误差。trace的使用 方法与quad相同。根据字符串order,对于相同的访问, dblquad能选择使用quad、quad8和许多用户定义的积分 方法,并返回与guad相同的变量。 输入quaddemo可以看到一个演示实例。 ■例11.1 下面用不同的方法来计算下列积分: (a)使用trapzt命令。首先创建一个有x值的向量。用5和l0两个值进行计算: x5=1 inspace(0,1,5);x10=1 inspace(0,1,10); 然后创建x的函数y: y5=exp(-x5.2);y10=exp(-x10.2); 现在计算出积分值: format long; integral5 trapz(x5,y5),... integral10 trapz(x10,y10) 返回 integral5 0.74298409780038 integral10 0.74606686791267 (b)使用guad命令。首先在M文件中创建函数。此文件integrand.m包含函数,如下: function y integrand(x) y =exp(-x.-2); 首先以标准误差计算积分,然后再以指定误差计算积分。 format long; integralStd quad('integrand',0,1) integralTol quad('integrand',0,1,0.00001)
q u a d 8 (. . .) 可以与q u a d一样用于相同的参数组合并返回相同的结果, 但使用更高精度的方法。因此,如果被积函数的导数在某一 区间内是不定的,例如: ,使用此命令将会更好 一些。q u a d和quad8 都要求被积函数在整个区间里是有限的。 dblquad(f, min1,计算双变量函数f的二重积分。函数中的第一个自变量用于 m a x 1 , m i n 2 , m a x 2 , 内层积分。内层积分在m i n1 和m a x1之间进行,外层积分在 t o l , t r a c e , o r d e r ) m i n2和m a x2之间进行。变量t o l指定相对误差。 t r a c e的使用 方法与 q u a d相同。根据字符串 o r d e r,对于相同的访问, d b l q u a d能选择使用q u a d、q u a d 8和许多用户定义的积分 方法,并返回与q u a d相同的变量。 输入q u a d d e m o可以看到一个演示实例。 ■ 例11 . 1 下面用不同的方法来计算下列积分: (a) 使用t r a p z命令。首先创建一个有x值的向量。用5和1 0两个值进行计算: 然后创建x的函数y: 现在计算出积分值: (b) 使用q u a d命令。首先在M文件中创建函数。此文件i n t e g r a n d . m包含函数,如下: 首先以标准误差计算积分,然后再以指定误差计算积分。 q = sinx 0 1 ò dx 1 5 2 M ATLAB 5 手册 下载 返回

China-pub.com 第11章积分和微分方程组 153 下载 给出 integralStd 0.74682612052747 integralTol 0.74682414517798 (c)使用quad8命令:使用在(b)中创建的M文件,然后输入: integral8Std quad8('integrand',0,1) integral8Std 0.74682413281243 这是MATLAB所能给出的最精确的结果。 (d使用cumtrapz命令能很容易地计算出不同区间的积分。 x=0:5; cumtrapz(x) ans 00.5000 2.0000 4.5000 8.0000 12.5000 (e)计算二重积分: 如图11-l。首先创建一个包含函数M文件:integrand.2.m: function y integrand2(x,y) y=exp(-x.2-y.2); 然后用quad命令计算对于固定的x值在y方向的一些积分值: x=linspace(0,1,15); for1=1:15 integral(i)=quad('integrand2',0,1,[],[],x(i)) end 现在已计算出在y方向的15个积分值。trapz命令能使用这些值来计算二重积分: format short; dIntegral trapz(x,integral) dIntegral 0.5575 输入下列语句可以得到一个积分区域的图形: [X,Y]=meshgrid(0:.1:1,0:.1:1); Z =integrand2(X,Y); mesh(X,Y,Z);view(30,30);
(c) 使用q u a d 8命令:使用在( b )中创建的M文件,然后输入: 这是M AT L A B所能给出的最精确的结果。 (d) 使用c u m t r a p z命令能很容易地计算出不同区间的积分。 (e) 计算二重积分: 如图11 - 1。首先创建一个包含函数M文件:i n t e g r a n d 2 . m: 然后用q u a d命令计算对于固定的x值在y方向的一些积分值: 现在已计算出在y方向的1 5个积分值。t r a p z命令能使用这些值来计算二重积分: 输入下列语句可以得到一个积分区域的图形: 第11章 积分和微分方程组 1 5 3 下载 给出

154 China-pub.coM MATLAB5手册 下载 结果如图11-1所示。命令mesh和view定义在13.5节中。 0.日 0. 。0 图11-1函数e2在区间[0,1]×[0,1]的上的图形 ■ 不定积分 ∫f)d不能使用上面的命令来计算。MATLAB中的数学符号工具箱和 MATLAB的编辑器能提供处理这些积分的命令。 11.2常微分方程组 下面来研究常微分方程系统ODE,该系统处理的是初始值已知的一阶微分方程。在本节中 主要讨论这种类型的微分方程,同时也会举出两个有关边界值问题的例子。可以利用ODE系 统创建稀疏线性系统方程来求解这些例子。 在数学符号工具箱中,有一些命令能给出常微分方程的符号解,即解以数学表达式的形式给出。 在下面的初始值问题中,有两个未知函数:x1()和x2(),并用以下式子表达其微分形式: d水i二x对 d 在许多应用中,独立变量参数表示时间。 x=f(x1,x2,t) x2=f2(x1,x2,t) x1(0)=x1,0 x2(0)=x2,0 高阶的ODE能表达成第1阶的ODE系统。例如,有以下微分方程: x”=f(x,x',t) x(0)=x0 x'(to)=xpo 用x替换x‘用x,替换x,就能得到: [x1=2 x2=f(x1,x2,t) x1(0)=x0 x2(0)=xp0
结果如图11 - 1所示。命令m e s h和v i e w定义在1 3 . 5节中。 图11-1 函数e -x2 -y2在区间[ 0,1 ]×[ 0,1 ]的上的图形 不定积分 不能使用上面的命令来计算。 M AT L A B中的数学符号工具箱和 M AT L A B的编辑器能提供处理这些积分的命令。 11.2 常微分方程组 下面来研究常微分方程系统 O D E, 该系统处理的是初始值已知的一阶微分方程。在本节中 主要讨论这种类型的微分方程,同时也会举出两个有关边界值问题的例子。可以利用 O D E系 统创建稀疏线性系统方程来求解这些例子。 在数学符号工具箱中,有一些命令能给出常微分方程的符号解,即解以数学表达式的形式给出。 在下面的初始值问题中,有两个未知函数:x 1(t)和x 2(t),并用以下式子表达其微分形式: 在许多应用中,独立变量参数 t表示时间。 高阶的O D E能表达成第1阶的O D E系统。例如,有以下微分方程: 用x2替换x 用x1替换 x,就能得到: f(t) a x ò dt 1 5 4 M ATLAB 5 手册 下载 dxi dt = x ¢ i ■

China-pub.coM 第11章积分和微分方程组 155 下载 这是一个第1阶的ODE系统。 对于某一时间间隔0≤1≤T,初始值问题的解决方法是将时间分成一组有限和离散的时间 点,例如用相同的时间间隔△进行等分: t=i△t,i=0,.,W 其中时间步长△仁TN,N为某一整数。这种导数能被微分方程的可微分的商所代替,微分 方程表示在不同时间点的解。见例11.2,给出更多的有关有限微分商的信息。这种方法的稳 定性取决于△的大小和所采用的数值方法,用这种方法能得到ODE的近似值。 在许多应用中有一些微分过程非常复杂的微分方程,在某些区域里这些方程要求有非常 小的时间步长△1。解决这些问题的困难在于问题中涉及不同的时间尺度,如解的导数可能有 较大的变化。 MATLAB使用龙格-库塔-芬尔格(Runge-Kutta-Fehlberg)方法来解ODE问题。在有限点内 计算求解,而这些点的间距由解本身来决定。当解比较平滑时,区间内使用的点数少一些: 在解变化很快时,区间内应使用较多的点。 为了得到更多的有关何时使用哪种解法和算法的信息,推荐使用helpdesk。所有求解 方程通用的语法或句法在命令集108中头两行给出。时间间隔将以向量t=[t0,tt]给出。 命令ode23可以求解(2,3)阶的常微分方程组,函数ode45使用(4,5)阶的龙格-库塔-芬 尔格方法。注意,在这种情况下x是x的微分,不是x的转置。 在命令集108中so1ver将被诸如ode45函数所代替。 命令集108 龙格-库塔-芬尔格方法 [time,x]= 计算ODE或由字符串str给定的ODE的值。部分解已 solver(str,t,x0) 在向量time中给出。在向量time中给出部分解,包含的 是时间值。还有部分解在矩阵X中给出,X的列向量是 每个方程在这些值下的解。对于标量问题,方程的解将 在向量X中给出。这些解在时间区间(1)到t(2)上计算得 到,其初始值是x0即x(t(1)。此方程组由str指定的M文 件中函数表示出。这个函数需要两个参数:标量1和向 量x,应该返回向量x'(即x的导数)。因为对标量ODE来 说,x和x'都是标量。在M文件中输入odefile可得到 更多信息。同时可以用命令numjac来计算雅可比函 数。 [t,X]= 此方程的求解过程同上。结构val包含用户给solver solver(str,t,x0,val) 的命令。参见odeset和表11-1,可得更多信息。 ode45 此方法被推荐为首选方法。 ode23 这是一个比ode45低阶的方法。 ode113 用于更高阶或大的标量计算。 ode23t 用于解决难度适中的问题。 ode23s 用于解决难度较大的微分方程组。对于系统中存在常 量矩阵的情况也有用
这是一个第1阶的O D E系统。 对于某一时间间隔0≤t≤T,初始值问题的解决方法是将时间分成一组有限和离散的时间 点,例如用相同的时间间隔 Dt进行等分: 其中时间步长Dt=T / N,N为某一整数。这种导数能被微分方程的可微分的商所代替,微分 方程表示在不同时间点的解。见例 11 . 2,给出更多的有关有限微分商的信息。这种方法的稳 定性取决于Dt的大小和所采用的数值方法,用这种方法能得到 O D E的近似值。 在许多应用中有一些微分过程非常复杂的微分方程,在某些区域里这些方程要求有非常 小的时间步长 Dt。解决这些问题的困难在于问题中涉及不同的时间尺度,如解的导数可能有 较大的变化。 M AT L A B使用龙格-库塔-芬尔格(R u n g e - K u t t a - F e h l b e rg)方法来解O D E问题。在有限点内 计算求解,而这些点的间距由解本身来决定。当解比较平滑时,区间内使用的点数少一些; 在解变化很快时,区间内应使用较多的点。 为了得到更多的有关何时使用哪种解法和算法的信息,推荐使用 h e l p d e s k。所有求解 方程通用的语法或句法在命令集 1 0 8中头两行给出。时间间隔将以向量 t = [ t 0 , t t ]给出。 命令o d e 2 3可以求解( 2,3 )阶的常微分方程组,函数 o d e 4 5使用( 4,5 )阶的龙格-库塔-芬 尔格方法。注意,在这种情况下 x´是x的微分,不是x的转置。 在命令集1 0 8中s o l v e r将被诸如o d e 4 5函数所代替。 命令集1 0 8 龙格-库塔-芬尔格方法 [ t i m e , X ]= 计算O D E或由字符串s t r给定的O D E的值。部分解已 s o l v e r ( s t r , t , x 0 ) 在向量t i m e中给出。在向量t i m e中给出部分解,包含的 是时间值。还有部分解在矩阵 X中给出,X的列向量是 每个方程在这些值下的解。对于标量问题,方程的解将 在向量X中给出。这些解在时间区间t ( 1 )到t ( 2 )上计算得 到,其初始值是x 0即x ( t ( 1 ) )。此方程组由s t r指定的M文 件中函数表示出。这个函数需要两个参数:标量 t和向 量x,应该返回向量x' (即x的导数)。因为对标量O D E来 说,x和x'都是标量。在M文件中输入o d e f i l e可得到 更多信息。同时可以用命令 n u m j a c来计算雅可比函 数。 [ t , X ] = 此方程的求解过程同上。结构 v a l包含用户给s o l v e r s o l v e r ( s t r , t , x 0 , v a l ) 的命令。参见o d e s e t和表11 - 1,可得更多信息。 o d e 4 5 此方法被推荐为首选方法。 o d e 2 3 这是一个比o d e 4 5低阶的方法。 o d e 1 1 3 用于更高阶或大的标量计算。 o d e 2 3 t 用于解决难度适中的问题。 o d e 2 3 s 用于解决难度较大的微分方程组。对于系统中存在常 量矩阵的情况也有用。 第11章 积分和微分方程组 1 5 5 下载

156 MATLAB5手册 China-pub.c 下载 ode15s 与ode23s相同,但要求的精度更高。 ode23tb 用于解决难度较大的问题。对于系统中存在常量矩阵 的情况也有用。 set=odeset(set1,val1,返回结构set,其中包含用于0DE求解方程的设置参数。 set2,va12,···) 有关可用设置的信息参见表11-1。 odeget (set,'set1') 返回结构set中设置setl的值 有许多设置对odeset控制的0DE解是有用的,参见表I1-l。例如,如果在求解过程中要 画出解的图形,可以输入:inst=odeset(OutputFcn','odeplot');。 表11-1ODE求解方程的设置参数 RelTol 给出求解方程允许的相对误差 AbsTol 给出求解方程允许的绝对误差 Refine 给出与输出点数相乘的因子 OutputFcn 这是一个带有输出函数名的字符串,该字符串将在求解函数执行的每 步被调用:odephas2(画出2D的平面相位图),odephas3(画出3D的平面 相位图),odeplot(画出解的图形),odeprint(显示中间结果) Outputsel 是一个整型向量,指出哪些元素应被传递给函数,特别是传递综utputFcn Stats 如果参数Stats为on,则将统计并显示出计算过程中资源消耗情况 Jacobian 如果编写ODE文件代码以便E(t,y,'jacobian')返回dF1d,则将 Jacobian设置为on Jconstant 如果雅可比数d切d是常量,则将此参数设置为on JPattern 如果编写ODE文件的编码以便函数E(I],[],'jpattern') 返回带 有零的稀疏矩阵并输出非零元素dFIdy,则需将Jpatterni设置成on Vectorized 如果编写ODE文件编码以便函数E(t,[y1,y2'··]返回 [F(t,y1)E(t,y2门,则将此参数设置成on Events 如果ODE文件中有带有参数‘events',则将此参数设置成on Mass 如果编写ODE文件编码以实现函数E(t,[】,mass')返回M和M(), 应将此参数设置成on MassConstant 如果矩阵M1)是常量,则将此参数设置为on MaxStep 此参数是限定算法能使用的区间长度上限的标量 Initialstep 给出初始步长的标量。如果给定的区间太大,算法就使用一个较小的步长 Maxorder 此参数只能被odel5s使用,它主要是指定ode15s的最高阶数,并且此参 数应是从1到5的整数 BDE 此参数只能被odel5s使用。如果使用倒推微分公式而不是使用通常所 使用的微分公式,则要将它设置为on NormControl 如果算法根据norm(e)<=max(RelTol+norm(y),AbsTo1)来步积 分过程中的错误,则要将它设置为on 也可试用命令odedemo
o d e 1 5 s 与o d e 2 3 s相同,但要求的精度更高。 o d e 2 3 t b 用于解决难度较大的问题。对于系统中存在常量矩阵 的情况也有用。 s e t = o d e s e t ( s e t 1 , v a l 1 , 返回结构s e t,其中包含用于O D E求解方程的设置参数。 s e t 2 , v a l 2 ,. . .) 有关可用设置的信息参见表 11 - 1。 o d e g e t ( s e t ,’s e t 1’) 返回结构s e t中设置s e t 1的值 有许多设置对o d e s e t控制的O D E解是有用的,参见表11 - 1。例如,如果在求解过程中要 画出解的图形,可以输入: i n s t = o d e s e t (‘O u t p u t F c n’,’o d e p l o t’) ;。 表11-1 ODE求解方程的设置参数 R e l T o l 给出求解方程允许的相对误差 A b s T o l 给出求解方程允许的绝对误差 R e f i n e 给出与输出点数相乘的因子 O u t p u t F c n 这是一个带有输出函数名的字符串,该字符串将在求解函数执行的每 步被调用:o d e p h a s 2(画出2 D的平面相位图 ) , o d e p h a s 3 (画出3 D的平面 相位图) ,o d e p l o t(画出解的图形) ,o d e p r i n t(显示中间结果) O u t p u t S e l 是一个整型向量,指出哪些元素应被传递给函数,特别是传递给O u t p u t F c n S t a t s 如果参数S t a t s为o n,则将统计并显示出计算过程中资源消耗情况 J a c o b i a n 如果编写O D E文件代码以便F ( t , y ,’j a c o b i a n’)返回d F/d y,则将 J a c o b i a n设置为o n J c o n s t a n t 如果雅可比数d f/d y是常量,则将此参数设置为 o n J P a t t e r n 如果编写 O D E文件的编码以便函数 F ( [ ] , [ ] , ’ j p a t t e r n ’ ) 返回带 有零的稀疏矩阵并输出非零元素 d F/d y,则需将J p a t t e r n设置成o n V e c t o r i z e d 如果编写 O D E文件编码以便函数 F ( t , [ y 1 , y 2 ’. . .] )返回 [F(t,y1) F(t,y2). . .],则将此参数设置成o n E v e n t s 如果O D E文件中有带有参数‘e v e n t s’,则将此参数设置成o n M a s s 如果编写O D E文件编码以实现函数 F ( t , [ ] ,’m a s s’)返回M和M(t), 应将此参数设置成o n M a s s C o n s t a n t 如果矩阵M(t)是常量,则将此参数设置为 o n M a x S t e p 此参数是限定算法能使用的区间长度上限的标量 I n i t i a l S t e p 给出初始步长的标量。如果给定的区间太大,算法就使用一个较小的步长 M a x O r d e r 此参数只能被o d e 1 5 s使用,它主要是指定o d e 1 5 s的最高阶数,并且此参 数应是从1到5的整数 B D F 此参数只能被 o d e 1 5 s使用。如果使用倒推微分公式而不是使用通常所 使用的微分公式,则要将它设置为 o n N o r m C o n t r o l 如果算法根据n o r m ( e ) < = m a x ( R e l T o l*n o r m ( y ) , A b s T o l )来步积 分过程中的错误,则要将它设置为 o n 也可试用命令o d e d e m o。 1 5 6 M ATLAB 5 手册 下载

China-bub.com 第11章积分和微分方程组 157 下载 ■例11.2 (a)求解下面的ODE: x/=-x2 x(0)=1 创建函数xprim1,将此函数保存在M文件xpriml.m中: function xprim xprimi(t,x) xprim -x.2; 然后,调用MATLAB的ODE算法求解方程,最后画出解的图形: [t,x]=ode45('xprim1',[01],1); p1ot(t,x,’-’,t,x,’0); xlabel('time to =0,tt =1'); ylabel('x values x(0)=1'); 得到图11-2。MATLAB计算出的解用圆圈标记。在13.1节中介绍绘图命令p1ot。 05 05 0.7 a85 06 Q10.2030.4·050.6070.809 m80=0量=1 图1l-2由函数xprim1定义的ODE解的图形 (b)解下面的ODE过程是等价的: [x'=x2 x(0)=1 首先创建函数xprim.2,并将其保存在M文件xprim2.m中: function xprim xprim2(t,x) xprim x.2; 然后调用ODE的求解方程并画出其解的图形:
■ 例11 . 2 (a) 求解下面的O D E: 创建函数x p r i m1,将此函数保存在M文件x p r i m 1 . m中: 然后,调用M AT L A B的O D E算法求解方程,最后画出解的图形: 得到图11 - 2。M AT L A B计算出的解用圆圈标记。在 1 3 . 1节中介绍绘图命令p l o t。 图11-2 由函数x p r i m 1定义的O D E解的图形 (b) 解下面的O D E过程是等价的: 首先创建函数x p r i m2,并将其保存在M文件x p r i m 2 . m中: 然后调用O D E的求解方程并画出其解的图形: 第11章 积分和微分方程组 1 5 7 下载
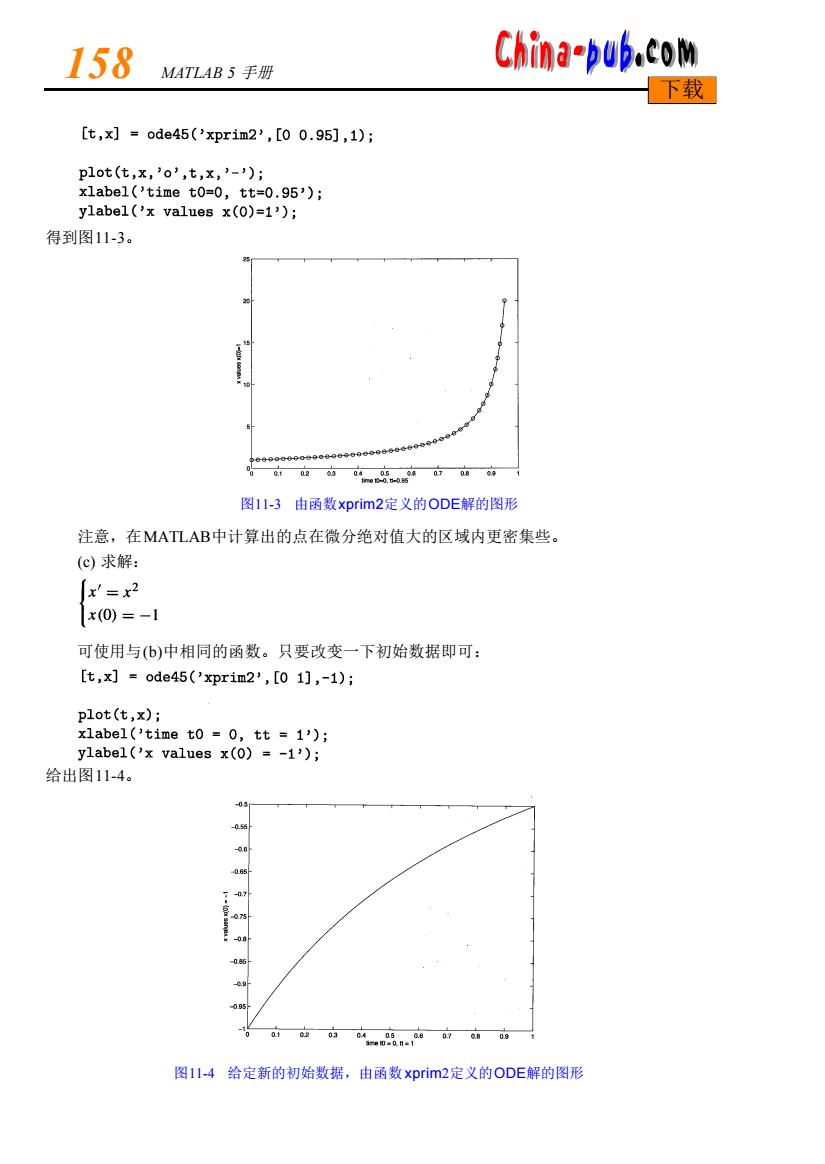
158 China-bub.com MATLAB5手册 下载 [t,x]=ode45('xprim?2',[00.95],1); p1ot(t,x,'o’,t,x,3-); xlabel('time to=0,tt=0.95'); ylabel('x values x(0)=1'); 得到图11-3。 图11-3由函数xprim2定义的ODE解的图形 注意,在MATLAB中计算出的点在微分绝对值大的区域内更密集些。 (c)求解: x'=x2 x(0)=-1 可使用与(b)中相同的函数。只要改变一下初始数据即可: [t,x]=ode45('xprim2',[01],-1); plot(t,x); xlabel('time to =0,tt =1'); ylabel('x values x(0)=-1'); 给出图11-4。 -05 0 a65 Q75 086 1020904050807809 nwo。0.Hs1 图11-4给定新的初始数据,由函数xprim2定义的ODE解的图形
得到图11 - 3。 图11-3 由函数x p r i m 2定义的O D E解的图形 注意,在M AT L A B中计算出的点在微分绝对值大的区域内更密集些。 (c) 求解: 可使用与( b )中相同的函数。只要改变一下初始数据即可: 给出图11 - 4。 图11-4 给定新的初始数据,由函数 x p r i m2定义的O D E解的图形 1 5 8 M ATLAB 5 手册 下载
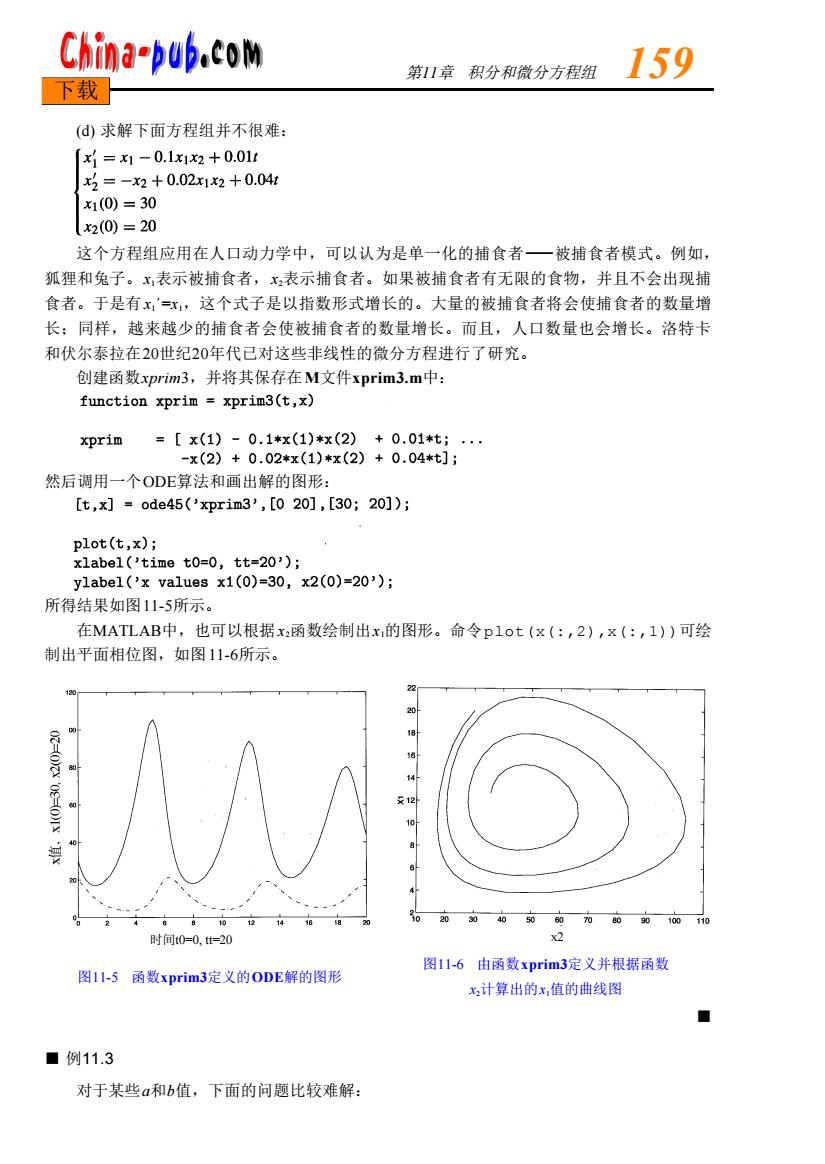
China-pub.com 第11章积分和微分方程组 159 下载 (d)求解下面方程组并不很难: =1-0.1x1x2+0.011 x=-x2+0.02x1x2+0.04 x1(0)=30 x2(0)=20 这个方程组应用在人口动力学中,可以认为是单一化的捕食者一被捕食者模式。例如, 狐狸和兔子。x表示被捕食者,x2表示捕食者。如果被捕食者有无限的食物,并且不会出现捕 食者。于是有x,'=x,这个式子是以指数形式增长的。大量的被捕食者将会使捕食者的数量增 长:同样,越来越少的捕食者会使被捕食者的数量增长。而且,人口数量也会增长。洛特卡 和伏尔泰拉在20世纪20年代已对这些非线性的微分方程进行了研究。 创建函数xprim3,并将其保存在M文件xprim3.m中: function xprim xprim3(t,x) xpr1m=[x(1)-0.1*x(1)*x(2)+0.01*t;. -x(2)+0.02*x(1)*x(2)+0.04*t]; 然后调用一个ODE算法和画出解的图形: [t,x]=ode45('xprim3',[020],[30;20]); plot(t,x) xlabel('time to=0,tt=20'); y1abe1('x values x1(0)=30,x2(0)=20'); 所得结果如图11-5所示。 在MATLAB中,也可以根据x2函数绘制出x的图形。命令p1ot(x(:,2),x(:,1))可绘 制出平面相位图,如图11-6所示。 20 18 O-OIX 10 2030405060700901010 时间t0=0,t=20 X2 图11-6由函数xprim3定义并根据函数 图1l-5函数xprim3定义的ODE解的图形 x2计算出的x,值的曲线图 ■例11.3 对于某些α和b值,下面的问题比较难解:
(d) 求解下面方程组并不很难: 这个方程组应用在人口动力学中,可以认为是单一化的捕食者—被捕食者模式。例如, 狐狸和兔子。x1表示被捕食者,x2表示捕食者。如果被捕食者有无限的食物,并且不会出现捕 食者。于是有x1´ =x1,这个式子是以指数形式增长的。大量的被捕食者将会使捕食者的数量增 长;同样,越来越少的捕食者会使被捕食者的数量增长。而且,人口数量也会增长。洛特卡 和伏尔泰拉在2 0世纪2 0年代已对这些非线性的微分方程进行了研究。 创建函数x p r i m3,并将其保存在M文件x p r i m 3 . m中: 然后调用一个O D E算法和画出解的图形: 所得结果如图11 - 5所示。 在M AT L A B中,也可以根据x2函数绘制出x1的图形。命令p l o t ( x ( : , 2 ) , x ( : , 1 ) )可绘 制出平面相位图,如图11 - 6所示。 ■ 例11 . 3 对于某些a和b值,下面的问题比较难解: 第11章 积分和微分方程组 1 5 9 下载 图11-5 函数x p r i m 3定义的O D E解的图形 图11-6 由函数x p r i m 3定义并根据函数 x2计算出的x1值的曲线图 ■ 时间t0=0, tt=20 x2

160 MATLAB5手册 China-pub.com 下载 x1=a-(b+1)x1+xx2 =bx1-xx2 0 =1 0=3 方程由下面的M文件stiff1.m定义: function stiff=stiffl(t,x) global a; 号变量不能放入参数表中 global b; stiff=[0;0]; 号st1f必须是一个冒号向量 8tiff(1)=a-(b+1)*x(1)+x(1)2*x(2); stiff(2)=b*x(1)-x(1)2*x(2); 下面的M文件给出一个比较困难的问题: global a;a =100; global b;b =1; tic; [t,X]=ode23('stiff1',[010],[13]); toc size(t) 运行后得到的结果如下: elapsed_time 72.1647 ans 34009 1 使用专门解决复杂问题的解法ode23s,将会得到较好的结果: elapsed_time 1.0098 ans 103 1 ■ 对于边界值问题,除了微分方程,还有在边界处的值。在一维下这意味至少有两个条件。 现在举两个如下的例子: ·假设要研究一根杆的温度分布情况。这根杆一端的温度是T,另一端的温度是T1:如 图11-7所示。 令y(x)表示这根杆的温度,函数x)表示加热源。 从时间=O开始,在相当长的时间内加热这根杆,直至达到平衡状态。这就是所谓的定常 值或稳定状态。这个定常值可由下面的方程模型表示: -y"(x)=f(x),0<x<1 y(0)=T0 y(1)=T 假设这根杆两端为:x=0和x=1。 ·假设在其两端有一根固定的柱子(或者可以看成是一个连接两个岛屿的桥),如图11-8所示
方程由下面的M文件s t i ff 1 . m定义: function stiff=stiff1(t, x) global a; % 变量不能放入参数表中 global b; s t i f f = [ 0 ; 0 ] ; % Stiff必须是一个冒号向量 下面的M文件给出一个比较困难的问题: 运行后得到的结果如下: 使用专门解决复杂问题的解法 o d e 2 3 s,将会得到较好的结果: 对于边界值问题,除了微分方程,还有在边界处的值。在一维下这意味至少有两个条件。 现在举两个如下的例子: • 假设要研究一根杆的温度分布情况。这根杆一端的温度是 T0,另一端的温度是 T1;如 图11 - 7所示。 令y(x)表示这根杆的温度,函数f(x)表示加热源。 从时间t= 0开始,在相当长的时间内加热这根杆,直至达到平衡状态。这就是所谓的定常 值或稳定状态。这个定常值可由下面的方程模型表示: 假设这根杆两端为:x= 0和 x= 1。 • 假设在其两端有一根固定的柱子(或者可以看成是一个连接两个岛屿的桥),如图11-8所示。 1 6 0 M ATLAB 5 手册 下载 ■