
China-pub.com 下载 第10章 函数、插值和曲线拟合分析 MATLAB可以处理有估值和没有估值的多项式,还有一些强大的数值分析命令,如求零 值和最小值。MATLAB中还有数据集合的插值、曲线拟合的命令和函数,还提到了经典的贝 赛尔(Bessel)函数。 10.1 MATLAB中的多项式 MATLAB将阶为n的多项式px)存储在长度为n+I的行向量p中。元素为多项式的系数,并 按x的幂降序排列,表示为: p=(an an-1...al ao) 代表的多项式为: p(x)=anx"an-1x-I+...+aix+ao 令A是一个稀疏矩阵,向量p和q的长度分别为n+1和m+1,它们分别表示次数为n和m的多 项式。MATLAB中处理多项式的命令如下: 命令集99 多项式 polyval(p,x) 计算多项式P。如果x是一个标量,则计算出多项式在x点 的值:如果x是一个向量或者一个矩阵,则计算出多项式 在x中所有元素上的值。 [y,err]= 计算向量x的多项式p的值。同上,计算结果在y中,同时 polyval(p,x,E) 还根据polyfit命令给出的矩阵E返回一个误差估计向量 err。见help polyvaf和nelp polyfit参见10.4节。 polyvalm(p,A) 直接对矩阵A进行多项式计算。不是象上个命令一样对每个 元素进行多项式计算,而是计算p(A)=pA+BA-++pl。 poly(A) 计算矩阵A的特征多项式向量。 poly(x) 给出一个长度为+1的向量,其中的元素是次数为n的多项 式的系数。这个多项式的根是长度为n的向量x中元素。 compan (p) 计算带有系数P的多项式的友矩阵A,这个矩阵的特征多 项式为p。 roots(p) 计算特征多项式即的根,是一个长度为m的向量,也就是方程 0的解。表达式oly(roots(p)p为真。结果可以是复数。 conv(p,q) 计算多项式p和q的乘积,也可以认为是p和q的卷积。 [k,r]=deconv (p,q) 计算多项式p除q。k是商多项式,r是残数多项式。这个 计算等价于p和q的逆卷积
下载 第1 0章 函数、插值和曲线拟合分析 M AT L A B可以处理有估值和没有估值的多项式,还有一些强大的数值分析命令,如求零 值和最小值。M AT L A B中还有数据集合的插值、曲线拟合的命令和函数,还提到了经典的贝 赛尔( B e s s e l )函数。 10.1 MAT L A B中的多项式 M AT L A B将阶为n的多项式p ( x )存储在长度为n+ 1的行向量p中。元素为多项式的系数,并 按x的幂降序排列,表示为: 代表的多项式为: 令A是一个稀疏矩阵,向量 p和q的长度分别为n+ 1和m+ 1,它们分别表示次数为 n和m的多 项式。M AT L A B中处理多项式的命令如下: 命令集9 9 多项式 p o l y v a l ( p , x ) 计算多项式 p。如果x是一个标量,则计算出多项式在 x点 的值;如果 x是一个向量或者一个矩阵,则计算出多项式 在x中所有元素上的值。 [ y , e r r ] = 计算向量x的多项式p的值。同上,计算结果在y中,同时 p o l y v a l ( p , x , E ) 还根据p o l y f i t命令给出的矩阵E返回一个误差估计向量 e r r。见help polyval和help polyfit,参见1 0 . 4节。 p o l y v a l m ( p , A ) 直接对矩阵A进行多项式计算。不是象上个命令一样对每个 元素进行多项式计算,而是计算p(A) =p1An+p2An-1+…+pn + 1I。 p o l y ( A ) 计算矩阵A的特征多项式向量。 p o l y ( x ) 给出一个长度为n+ 1的向量,其中的元素是次数为 n的多项 式的系数。这个多项式的根是长度为 n的向量x中元素。 c o m p a n ( p ) 计算带有系数 p的多项式的友矩阵 A,这个矩阵的特征多 项式为p。 r o o t s ( p ) 计算特征多项式p的根,是一个长度为n的向量,也就是方程 p(x) = 0的解。表达式p o l y ( r o o t s ( p ) ) = p为真。结果可以是复数。 c o n v ( p , q ) 计算多项式p和q的乘积,也可以认为是p和q的卷积。 [ k , r ] = d e c o n v ( p , q ) 计算多项式 p除q。k是商多项式, r是残数多项式。这个 计算等价于p和q的逆卷积

136 China-pub.com MATLAB5手册 下载 [u v kF 计算px)/gx的部分展开式: residue(p,q) py-u四 ,u2) u) +k) q(x)x-n(1)x-n(2) x-n(i) 向量p和q分别是多项式px)和gx)的系数。得到的余数在 向量u中,极点在列向量v中,商多项式在向量k中。 [pg]=residue(u,v,x从同上的部分展开式u、v和x计算得到多项式p和qe mpoles 给出极点多样性的相关信息,见help mpo1es polyder(p) 计算得到长度为的微分多项式向量,多项式的系数在向量中。 polyder(p,q) 返回一个向量,它表示由conv(p,q)定义的多项式微分。 [u,v]=polyder(p,q)返回两个向量,它们表示由deconv(p,q)定义的多项式 微分,表达形式为uN。 ■例10.1 将一些多项式命令应用在下列的多项式上: p2(x)=3x2+2x-4p3x)=2x3-2 MATLAB用下列向量来表示这两个多项式: p2=[32-4]; p3=[200-2]; (a)计算多项式在x=l处的值,输入: value2 polyval(p2,1),... value3=polyval(p3,1) 结果为: value2 1 value3 0 (b)很容易对向量或者矩阵计算多项式的值,输入: x=[123]'; values2 polyval(p2,x),values3 polyval(p3,x) 结果为: values2 1 12 29 values3 0 14 52
[u v k]= 计算p ( x ) / q ( x )的部分展开式: r e s i d u e ( p , q ) 向量p和q分别是多项式 p ( x )和q ( x )的系数。得到的余数在 向量u中,极点在列向量v中,商多项式在向量k中。 [p q]=residue(u,v,x)从同上的部分展开式u、v和x计算得到多项式p和q。 m p o l e s 给出极点多样性的相关信息,见 help mpoles。 p o l y d e r ( p ) 计算得到长度为n的微分多项式向量,多项式的系数在向量p中。 p o l y d e r ( p , q ) 返回一个向量,它表示由c o n v ( p , q )定义的多项式微分。 [ u , v ] = p o l y d e r ( p , q ) 返回两个向量,它们表示由 d e c o n v ( p , q )定义的多项式 微分,表达形式为u/v。 ■ 例1 0 . 1 将一些多项式命令应用在下列的多项式上: M AT L A B用下列向量来表示这两个多项式: (a) 计算多项式在x= 1处的值,输入: 结果为: (b) 很容易对向量或者矩阵计算多项式的值,输入: 结果为: p(x) q(x) = u(1) x - n(1) + u(2) x - n(2) + ×××+ u(j) x - n(j) + k(x). 1 3 6 M ATLAB 5 手册 下载
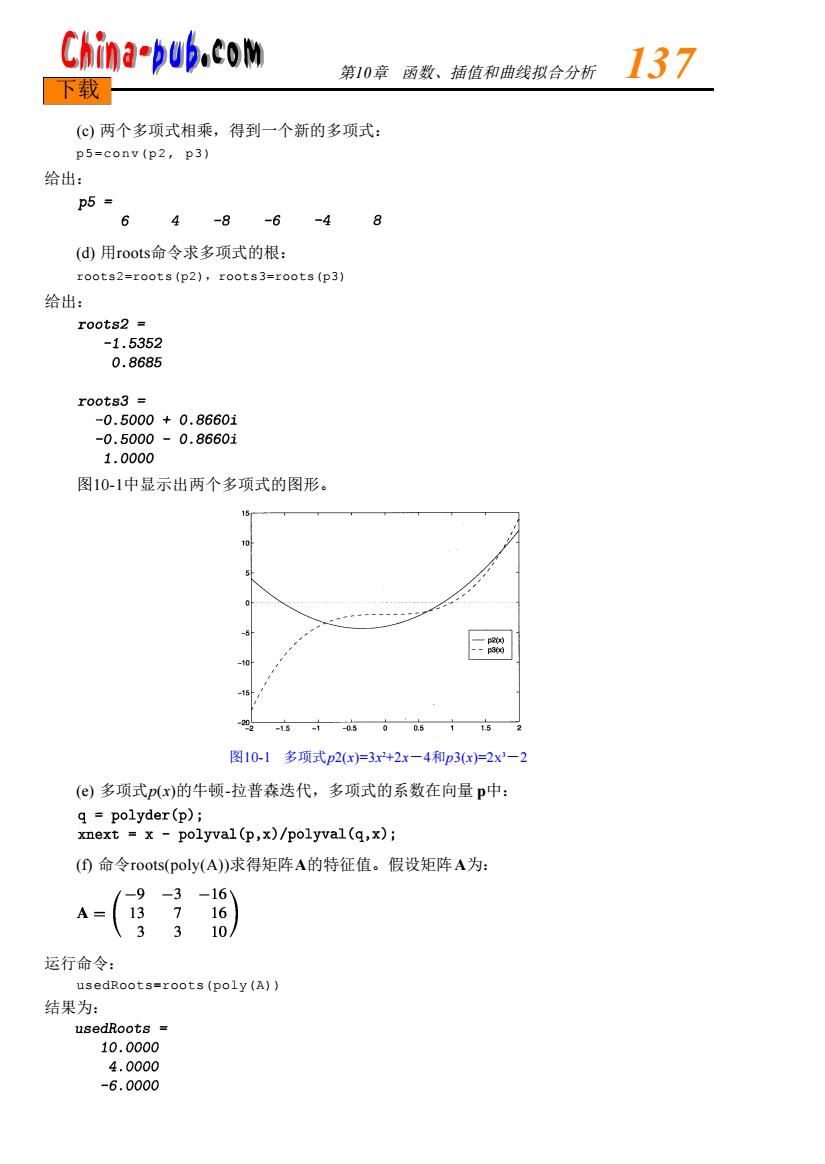
China-pub.com 第10章函数、插值和曲线拟合分析 137 下载 (©)两个多项式相乘,得到一个新的多项式: p5=conv(p2,p3) 给出: p5= 6 4 -8 -6 -4 (d)用rootst命令求多项式的根: roots2=roots(p2),roots3=roots(p3) 给出: roots2 -1.5352 0.8685 roots3= -0.5000+0.86601 -0.5000-0.86601 1.0000 图10-1中显示出两个多项式的图形。 15 一 0.5 1.5 图10-1多项式p2(x)=3x2+2x-4和p3(x)=2x3-2 (e)多项式p(x)的牛顿-拉普森迭代,多项式的系数在向量p中: q=polyder(p); xnext x -polyval(p,x)/polyval(q,x); ()命令roots(poly(A)求得矩阵A的特征值。假设矩阵A为: 运行命令: usedRoots=roots(poly(A)) 结果为: usedRoots 10.0000 4.0000 -6.0000
(c) 两个多项式相乘,得到一个新的多项式: p5=conv(p2, p3) 给出: (d) 用r o o t s命令求多项式的根: r o o t s 2 = r o o t s ( p 2 ),r o o t s 3 = r o o t s ( p 3 ) 给出: 图1 0 - 1中显示出两个多项式的图形。 图10-1 多项式p2 (x) = 3x 2+ 2x-4和p3 (x) = 2 x3-2 (e) 多项式p(x)的牛顿-拉普森迭代,多项式的系数在向量 p中: (f) 命令r o o t s ( p o l y ( A ) )求得矩阵A的特征值。假设矩阵A为: 运行命令: u s e d R o o t s = r o o t s ( p o l y ( A ) ) 结果为: 第1 0章 函数、插值和曲线拟合分析 1 3 7 下载

138 ATLAB5手册 China-pub.com 下载 然而这样得到的特征值没有用MATLAB命令eig(A)得到的特征值的精度高,而且有效 性也差些: usedEig=eig(A) 给出: usedEig -6.0000 10.0000 4.0000 结果是一样的,但是顺序正好相反。 (g)对于所有的矩阵A都有:po1yva1m(po1y(A),A)。=0 这是Cayley-Hamilton法则。这个法则对于秩为5的方阵来说: Magical magic(5); AlmostZero polyvalm(poly(Magical),Magical) AlmostZero 1.0e-07* 0.2794 0.3551 0.1723 0.1770 0.2654 0.2765 0.2887 0.2049 0.2142 0.2561 0.1775 0.2468 0.2701 0.3073 0.2375 0.1942 0.2744 0.2759 0.2608 0.2282 0.2082 0.3120 0.2608 0.2515 0.2049 ■ 10.2 函数的零值 MATLAB的M文件可以表示数学函数:参见2.9节。函数: 5x-6.4 9x x-0.4 g(x)= x-1.3)2+0.002+x3+0.03-x-0.922+0.005 如果输入下面的M文件g.m,这个函数就可以在MATLAB中调用: function y =g(x) y=(5.*x-6.4)./((x-1.3).2+0.002)+.. (9.*x)./(x.3+0.03)-,., (x-0.4)./((x-0.92).2+0.005); 使用元素运算符*、人、A、+和一定义MATLAB函数g。结果是如果这个函数被一个向量调用, 那么得到的结果也是一个向量。本章中提到的所MATLAB函数需要以这种方式来定义数学函数。 用plot命令可以画出函数的图形: x=linspace(0,2); 号生成向量x plot(x,g(x)); 号画g(x)图形 grid; 冬画格栅 title('The g(x)function 告给出图标题 或者使用fplot命令: p1ot(g,【02]): 号画g(x)图形 grid; 号画格栅 title('The g(x)functidn 号给出图标题
然而这样得到的特征值没有用 M AT L A B命令e i g ( A )得到的特征值的精度高,而且有效 性也差些: u s e d E i g = e i g ( A ) 给出: 结果是一样的,但是顺序正好相反。 (g) 对于所有的矩阵A都有:polyvalm(poly(A), A)=0 。 这是C a y l e y - H a m i l t o n法则。这个法则对于秩为5的方阵来说: ■ 10.2 函数的零值 M AT L A B的M文件可以表示数学函数;参见 2 . 9节。函数: 如果输入下面的M文件g . m,这个函数就可以在M AT L A B中调用: 使用元素运算符. *、. /、. ^、+和-定义M AT L A B函数g。结果是如果这个函数被一个向量调用, 那么得到的结果也是一个向量。本章中提到的所有M AT L A B函数需要以这种方式来定义数学函数。 用p l o t命令可以画出函数的图形: x=linspace(0, 2); % 生成向量x p l o t ( x , g ( x ) ) ; % 画g ( x )图形 g r i d ; % 画格栅 t i t l e ('The g(x) function') % 给出图标题 或者使用f p l o t命令: f p l o t ('g', [0 2]); % 画g ( x )图形 g r i d ; % 画格栅 t i t l e ('The g(x) function') % 给出图标题 1 3 8 M ATLAB 5 手册 下载
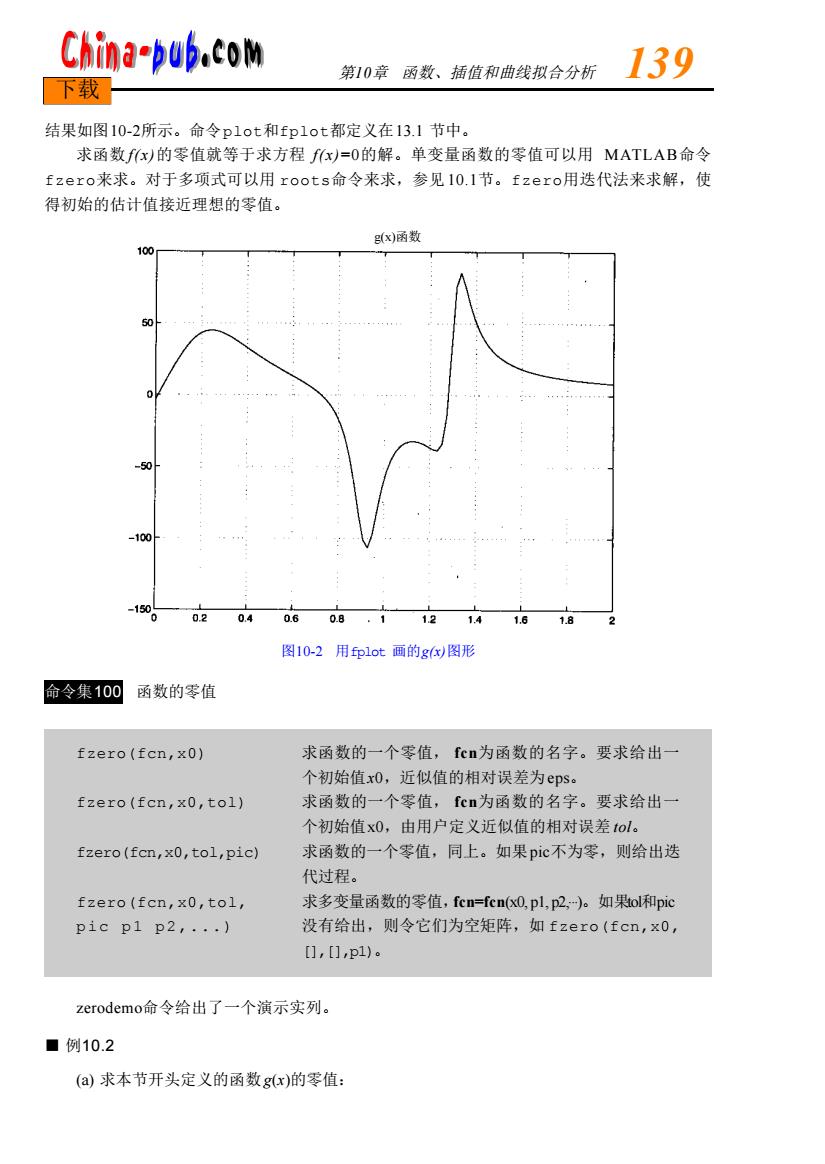
China-pub.com 第10章函数、插值和曲线拟合分析 139 下载 结果如图10-2所示。命令p1ot和fp1ot都定义在13.1节中。 求函数fx)的零值就等于求方程fx)=0的解。单变量函数的零值可以用MATLAB命令 fzero来求。对于多项式可以用roots命令来求,参见10.1节。fzero用迭代法来求解,使 得初始的估计值接近理想的零值。 g(x)函数 100 50 0.2 0.4 0.6 0.8 1 12 1.4 1.6 1.8 图10-2用p1ot画的gx)图形 命令集100 函数的零值 fzero(fcn,x0) 求函数的一个零值,fcn为函数的名字。要求给出一 个初始值x0,近似值的相对误差为eps。 fzero(fcn,x0,tol) 求函数的一个零值,fcn为函数的名字。要求给出一 个初始值x0,由用户定义近似值的相对误差tol。 fzero(fcn,x0,tol,pic) 求函数的一个零值,同上。如果pic不为零,则给出迭 代过程。 fzero(fcn,x0,tol, 求多变量函数的零值,fcn=fcn(x0,pl,p2,-)。如果ol和pic p1cp1p2,···) 没有给出,则令它们为空矩阵,如fzero(fcn,x0, [],[],p1)。 zerodemo命令给出了一个演示实列。 ■例10.2 (a)求本节开头定义的函数g(x)的零值:
结果如图1 0 - 2所示。命令p l o t和f p l o t都定义在13.1 节中。 求函数 f ( x )的零值就等于求方程 f ( x )= 0的解。单变量函数的零值可以用 M AT L A B命令 f z e r o来求。对于多项式可以用 r o o t s命令来求,参见 1 0 . 1节。f z e r o用迭代法来求解,使 得初始的估计值接近理想的零值。 图10-2 用f p l o t 画的g ( x )图形 命令集1 0 0 函数的零值 f z e r o ( f c n , x 0 ) 求函数的一个零值, f c n为函数的名字。要求给出一 个初始值x0,近似值的相对误差为e p s。 f z e r o ( f c n , x 0 , t o l ) 求函数的一个零值, f c n为函数的名字。要求给出一 个初始值x 0,由用户定义近似值的相对误差 t o l。 f z e r o ( f c n , x 0 , t o l , p i c ) 求函数的一个零值,同上。如果p i c不为零,则给出迭 代过程。 f z e r o ( f c n , x 0 , t o l , 求多变量函数的零值,f c n=f c n(x0, p1, p2,. . .)。如果t o l和p i c pic p1 p2,...) 没有给出,则令它们为空矩阵,如 f z e r o ( f c n , x 0 , [ ] , [ ] , p 1 )。 z e r o d e m o命令给出了一个演示实列。 ■ 例1 0 . 2 (a) 求本节开头定义的函数g(x)的零值: 第1 0章 函数、插值和曲线拟合分析 1 3 9 下载 g(x)函数
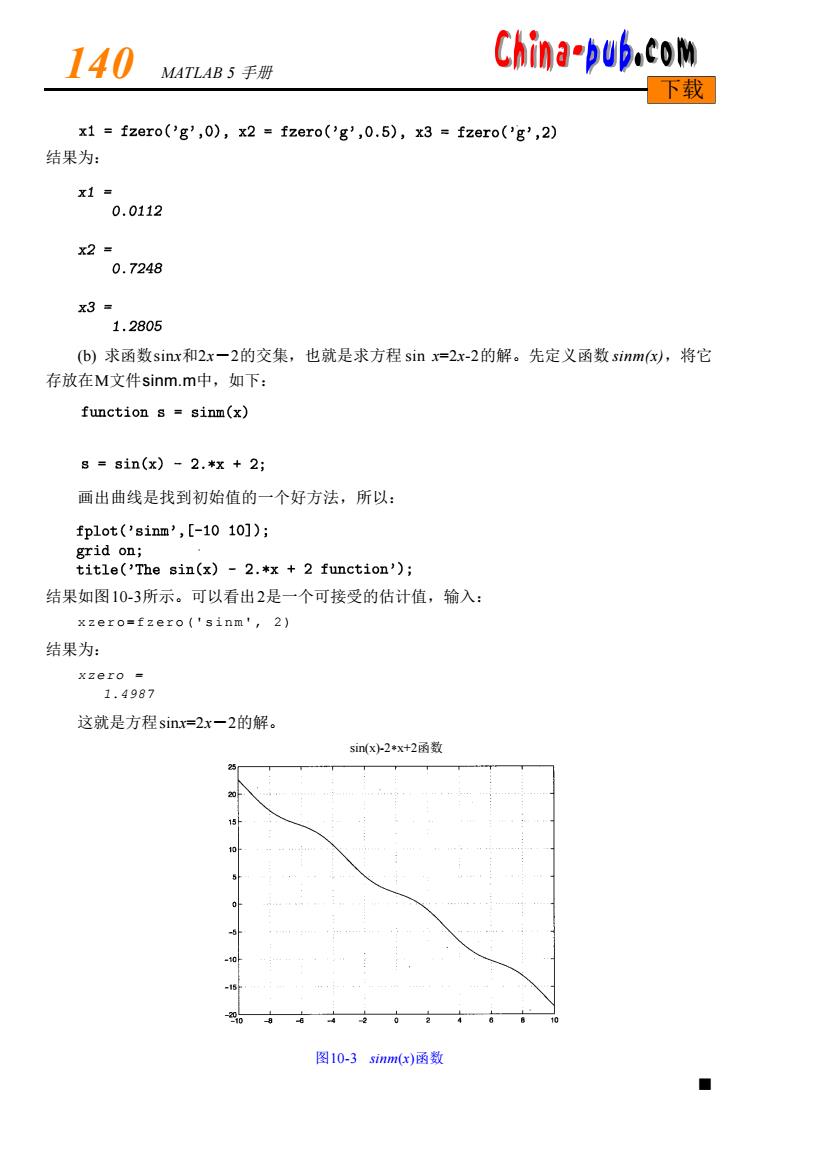
140 MATLAB5手册 China-pub.com 下载 x1 =fzero('g',0),x2 =fzero('g',0.5),x3 fzero('g',2) 结果为: x1= 0.0112 x2= 0.7248 x3= 1.2805 (b)求函数sinr和2x一2的交集,也就是求方程sinx=2x-2的解。先定义函数sinm(x,将它 存放在M文件sinm.m中,如下: function s sinm(x) s=sin(x)-2.*x+2; 画出曲线是找到初始值的一个好方法,所以: fplot('sinm',[-10 10]); grid on; title('The sin(x)-2.*x 2 function'); 结果如图10-3所示。可以看出2是一个可接受的估计值,输入: xzero=fzero('sinm',2) 结果为: xzero 1.4987 这就是方程sinx=2x一2的解。 sin(x-2*x+2函数 25 图10-3sinm(x)函数 ■
结果为: (b) 求函数s i nx和2x-2的交集,也就是求方程 sin x= 2x- 2的解。先定义函数 s i n m ( x ),将它 存放在M文件s i n m . m中,如下: 画出曲线是找到初始值的一个好方法,所以: 结果如图1 0 - 3所示。可以看出2是一个可接受的估计值,输入: xzero=fzero('sinm', 2) 结果为: xzero = 1 . 4 9 8 7 这就是方程s i nx= 2x-2的解。 图10-3 s i n m(x)函数 ■ 1 4 0 M ATLAB 5 手册 sin(x)-2*x+2函数 下载

China-pub.com 第10章函数、插值和曲线拟合分析 141 下载 10.3函数的最小值和最大值 最优化是求最优解,也就是在某个区间内有条件约束或者无条件约束地找到函数的最大 值或者最小值。MATLAB使用数字方法求函数的最小值。使用迭代算法,也就是有些步骤要 重复许多次。现在,假设要求函数f在某个区间内的最小值Xm。 f (xmin)=min f(x) 迭代方法需要一个初始估计值xo。从x开始找到一个更接近x的新值x,这个值的好坏取 决于使用的数学方法。直到找到有足够精度的近似值x,才停止迭代,也就是绝对值xm一x足 够小。 如果函数有多个局部最小值,fmin可以找到它们中的一个。也可用MATLAB的最优化工 具箱来求得,参见附录C。 这里提到了标准MATLAB系统的两个最优化命令,fmin命令可以求单变量函数的最小 值:fmins命令可以求多变量函数的最小值,同时它还要求有一个初始向量。 没有求函数f的最大值的命令,相反函数=一f的最小值可以求得。 命令集101 函数的最小值 fmin(fcn,x1,x2) 求函数在区间(xl,x2)内的最小值,fcn是目标函数名。如 果没有局部最小值,则返回区间内的最小x值。相对误差 小于10-。 fmin(fcn,x1,x2, 求函数在区间(xl,x2)内的最小值,fcn是目标函数名。 options) 如果没有局部最小值,则返回区间内的最小x值。向量 options为控制参数,如options(I)=l,显示中间结果: options(2)表示得到的结果x的精度,缺省为10-4。输入 help foption西得更多信息。 fmins(fcn,x0) 求函数fcn的最小值。由用户自己给出一个初始估计向量 x0,相对误差为10-4。 fmins (fcn,x0, 带优化参数求函数cn的最小值,同上。输入help fimins和 options) help foptions可得更多信息。例如,优化参数可以控 制迭代次数和计算结果的精度。 ■例10.3 (a)在区间[0,2]内求函数cos的最小值: cosmin=fmin('cos',0,+pa)号求cos的最小值 cosmin= 3.1416 这就是期望得到的结果。 (b)同样可以简单地求高级函数的最小值。对定义在10.2节中的函数gx),求在区间[0,2] 内的最小值
10.3 函数的最小值和最大值 最优化是求最优解,也就是在某个区间内有条件约束或者无条件约束地找到函数的最大 值或者最小值。 M AT L A B使用数字方法求函数的最小值。使用迭代算法,也就是有些步骤要 重复许多次。现在,假设要求函数 f在某个区间内的最小值xm i n。 迭代方法需要一个初始估计值 x0。从x0开始找到一个更接近 xm i n的新值x1,这个值的好坏取 决于使用的数学方法。直到找到有足够精度的近似值 xi才停止迭代,也就是绝对值 |xm i n-xi|足 够小。 如果函数有多个局部最小值, f m i n可以找到它们中的一个。也可用 M AT L A B的最优化工 具箱来求得,参见附录C。 这里提到了标准 M AT L A B系统的两个最优化命令, f m i n命令可以求单变量函数的最小 值;f m i n s命令可以求多变量函数的最小值,同时它还要求有一个初始向量。 没有求函数f的最大值的命令,相反函数 h=-f 的最小值可以求得。 命令集1 0 1 函数的最小值 f m i n ( f c n , x 1 , x 2 ) 求函数在区间(x1,x2 )内的最小值,f c n是目标函数名。如 果没有局部最小值,则返回区间内的最小 x值。相对误差 小于10-4。 f m i n ( f c n , x 1 , x 2 , 求函数在区间(x1,x2 )内的最小值,f c n是目标函数名。 o p t i o n s ) 如果没有局部最小值,则返回区间内的最小 x值。向量 o p t i o n s为控制参数,如 o p t i o n s( 1 ) = 1,显示中间结果; o p t i o n s( 2 )表示得到的结果 x的精度,缺省为 1 0-4。输入 help foptions可得更多信息。 f m i n s ( f c n , x 0 ) 求函数f c n的最小值。由用户自己给出一个初始估计向量 x 0,相对误差为1 0-4。 f m i n s ( f c n , x 0 , 带优化参数求函数f c n的最小值,同上。输入help fmins 和 o p t i o n s ) help f o p t i o n s可得更多信息。例如,优化参数可以控 制迭代次数和计算结果的精度。 ■ 例1 0 . 3 (a) 在区间[ 0,2 ]内求函数c o s的最小值: cosmin=fmin('cos', 0, 2 *pi) % 求c o s的最小值 c o s m i n = 3 . 1 4 1 6 这就是期望得到的结果。 (b) 同样可以简单地求高级函数的最小值。对定义在 1 0 . 2节中的函数g(x),求在区间[ 0,2 ] 内的最小值。 第1 0章 函数、插值和曲线拟合分析 1 4 1 下载

142 MATLAB5手册 China-bub.com 下载 gmin fmin('g',0,2) gmin 1.2277 注意,这是一个局部最小值,不一定是函数在这个区间内的最小值。从图10-2上可以看 出在一个更小区间内可以得到第二个最小值,这个值比第一个值还小: gmin2 fmin('g',0,1) gmin2= 0.9260 (c)还可以用fmin命令来求函数的最大值,但是要先编写一个返回一g(x)的函数,这个函 数保存在M文件minusg..m中。 function y minusg(x) y=-g(x); 求这个函数的最小值就等于求函数g的最大值。 gmax=fmin('minusg',0,2) 结果为: gmax 0.2433 在这个区间内有若干个最大值,MATLAB求出的最大值不一定是函数的全局最大值。 (d)用fmins命令来求多个变量函数的最小值,假设函数为: f(x1,x2)=x7+x3-0.5x1x2-sinx1 编写M文件fx1x2.m: function f fxix2(x) f=x(1).2+x(2).2-0.5.*x(1).*x(2)-sin(x(1)); 函数fmins要求有一个初始估计向量,假设给(1,0): fx1x2min fmins('fx1x2',[1,0]) 结果为: fx1x2min 0.4744 0.1186 用下面的程序画出函数的图形来: x=linspace(-1,150);号新建向量x,假设y=x for1=1:50 号计算fx1x2在每一点的值 for j=1:50 2(i,j)=fx1x2([×(i)×(j)]): end end meshc(x ,x,Z); 号带有基本等值线的网格图 view(80,10): 号指定观察点
注意,这是一个局部最小值,不一定是函数在这个区间内的最小值。从图 1 0 - 2上可以看 出在一个更小区间内可以得到第二个最小值,这个值比第一个值还小: (c) 还可以用f m i n命令来求函数的最大值,但是要先编写一个返回- g(x)的函数,这个函 数保存在M文件m i n u s g . m中。 求这个函数的最小值就等于求函数 g的最大值。 gmax=fmin('minusg', 0, 2) 结果为: 在这个区间内有若干个最大值, M AT L A B求出的最大值不一定是函数的全局最大值。 (d) 用f m i n s命令来求多个变量函数的最小值,假设函数为: 编写M文件f x 1 x 2 . m: 函数f m i n s要求有一个初始估计向量,假设给 ( 1,0 ): 结果为: 用下面的程序画出函数的图形来: x = l i n s p a c e (-1, 1 50); % 新建向量x,假设y = x for i=1: 50 % 计算f x 1 x 2在每一点的值 for j=1: 50 Z(i, j)=fx1x2([x(i) x(j)]); e n d end meshc(x ,x, Z); % 带有基本等值线的网格图 view(80, 10); % 指定观察点 1 4 2 M ATLAB 5 手册 下载
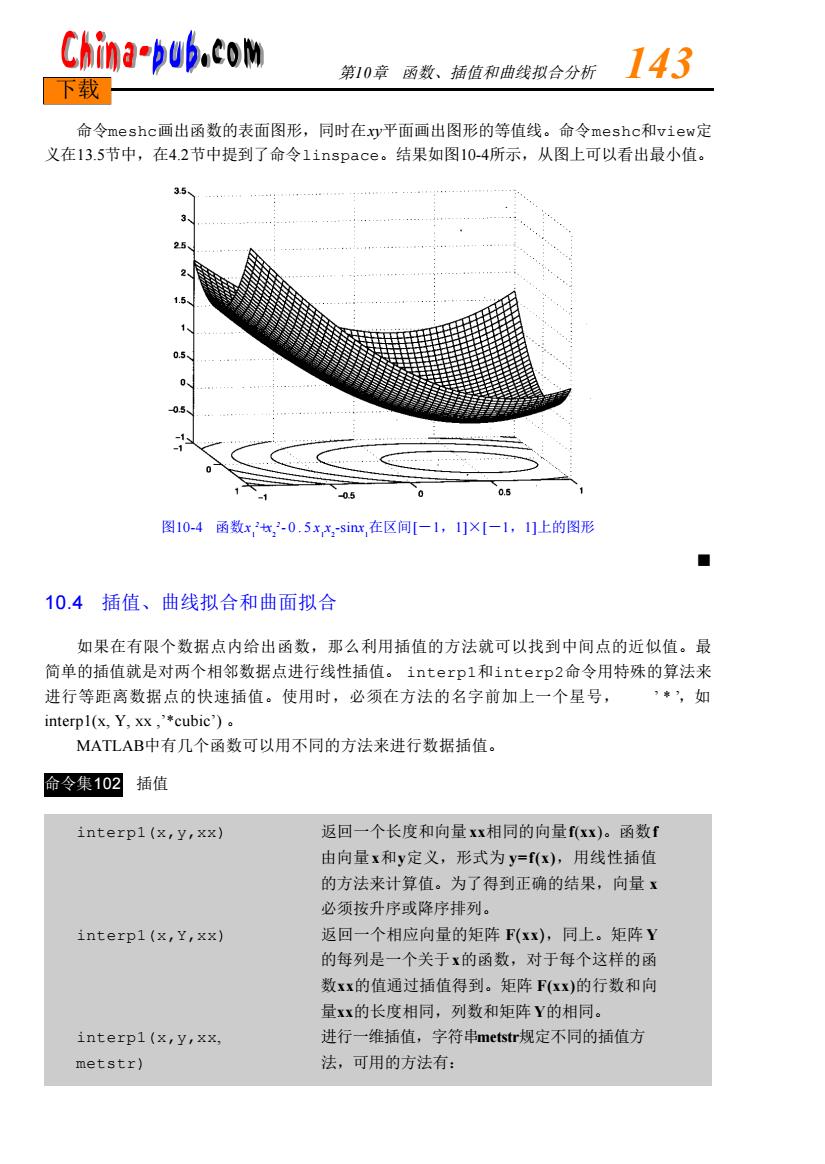
China-pub.com 第10章函数、插值和曲线拟合分析 143 下载 命令neshci画出函数的表面图形,同时在xy平面画出图形的等值线。命令meshc和view定 义在13.5节中,在4.2节中提到了命令1 inspace。结果如图10-4所示,从图上可以看出最小值。 35 25 05 0.5 .1 图10-4函数x2x2-0.5xx-sinx在区间[-1,1门×[-1,1]上的图形 ■ 10.4插值、曲线拟合和曲面拟合 如果在有限个数据点内给出函数,那么利用插值的方法就可以找到中间点的近似值。最 简单的插值就是对两个相邻数据点进行线性插值。interpl和interp.2命令用特殊的算法来 进行等距离数据点的快速插值。使用时,必须在方法的名字前加上一个星号, ’,如 interpl(x,Y,xx,'*cubic'). MATLAB中有几个函数可以用不同的方法来进行数据插值。 命令集102 插值 interpl(x,y,xx) 返回一个长度和向量xx相同的向量f(xx)。函数f 由向量x和y定义,形式为y=f(x),用线性插值 的方法来计算值。为了得到正确的结果,向量x 必须按升序或降序排列。 interpl(x,Y,xx) 返回一个相应向量的矩阵F(xx),同上。矩阵Y 的每列是一个关于x的函数,对于每个这样的函 数xx的值通过插值得到。矩阵F(xx)的行数和向 量xx的长度相同,列数和矩阵Y的相同。 interpl(x,y,xx, 进行一维插值,字符串metstr规定不同的插值方 metstr) 法,可用的方法有:
命令m e s h c画出函数的表面图形,同时在x y平面画出图形的等值线。命令m e s h c和v i e w定 义在1 3 . 5节中,在4 . 2节中提到了命令l i n s p a c e。结果如图1 0 - 4所示,从图上可以看出最小值。 图10-4 函数x 1 2+ x 2 2 - 0 . 5 x 1 x 2 - s i nx 1在区间[-1,1 ]×[-1,1 ]上的图形 ■ 10.4 插值、曲线拟合和曲面拟合 如果在有限个数据点内给出函数,那么利用插值的方法就可以找到中间点的近似值。最 简单的插值就是对两个相邻数据点进行线性插值。 i n t e r p 1和i n t e r p 2命令用特殊的算法来 进行等距离数据点的快速插值。使用时,必须在方法的名字前加上一个星号, ’ * ’,如 interp1(x, Y, xx ,’*cubic’) 。 M AT L A B中有几个函数可以用不同的方法来进行数据插值。 命令集1 0 2 插值 i n t e r p 1 ( x , y , x x ) 返回一个长度和向量x x相同的向量f(x x)。函数f 由向量x和y定义,形式为 y=f ( x ),用线性插值 的方法来计算值。为了得到正确的结果,向量 x 必须按升序或降序排列。 i n t e r p 1 ( x , Y , x x ) 返回一个相应向量的矩阵 F(x x),同上。矩阵 Y 的每列是一个关于x的函数,对于每个这样的函 数x x的值通过插值得到。矩阵 F ( x x )的行数和向 量x x的长度相同,列数和矩阵Y的相同。 i n t e r p 1 ( x , y , x x, 进行一维插值,字符串m e t s t r规定不同的插值方 m e t s t r ) 法,可用的方法有: 第1 0章 函数、插值和曲线拟合分析 1 4 3 下载

144 MATLAB5手册 China-pub.com 下载 ‘1 inear' 线性插值。 ‘nearest' 最邻近插值。 ‘spline' 三次样条插值。也叫外推法。 ‘cubic' 三次插值,要求x的值等距离。 所有插值方法均要求x是单调的。 interplq(x,y,xx) 和interpl相同,但是对于非均匀空间的数据插 值更快。 interp2(X,Y,Z,Xx, 进行矩阵Xx和Yy的二维插值,并由X、Y和Z Yy) 所描述的函数Z=X,)内的插值所决定。如果X、 Y和Z中任何一个是一个向量,则它的元素被认 为应用于相应的行和列。 interp2 (X,Y,Z,Xx, 进行二维插值,字符串metstr规定了不同的插 Yy,metstr) 值方法,可用的方法有: ‘1 inear' 线性插值。 ‘nearest' 最邻近插值。 ‘spline' 三次样条插值。 ‘cubic' 三次插值。 VV=interp3 (X,Y,Z, 进行由X,Y和Z所描述的函数V的插值,XX、 V,XX,YY,ZZ YY和ZZ是插值点。字符串metstr规定了不同 metstr) 的插值方法,可用的方法有: nearest' 使用最邻近点的值。 “linear' 使用8个最邻近点进行线性插值。 'spline' 三次样条插值。 cubic' 使用64个最邻近点进行三次插值。 VV=interpn (X1,X2, 和interp.3相同,但是V和VV可以是多维数组。 X3,···,V,Y1,,Y2, 如果X1,X2,X3,是等距离的,使用星号*如 Y3,···,method) *cub阿以加快计算速度。 Interpft(y,n) 快速傅利叶变换插值,返回一个长度为n,从y计 算得到的向量。要求y的值是等距离的,结果在 与y相同区间内计算。 griddata(x,y,z, 返回相同大小的矩阵Xx和Yy,它们表示一个网 Xx,Yy,'method') 格,由函数z=fc,的插值得到。向量x、y和z 包含的是三维空间的x、y和z坐标。字符串 method规定了不同的插值方法,可用的方法如 下: ‘1 inear' 基于三角的线性插值。 ‘nearest' 最邻近插值
‘l i n e a r’ 线性插值。 ‘n e a r e s t’ 最邻近插值。 ‘s p l i n e’ 三次样条插值。也叫外推法。 ‘c u b i c’ 三次插值,要求x的值等距离。 所有插值方法均要求x是单调的。 i n t e r p 1 q ( x , y , x x ) 和i n t e r p 1相同,但是对于非均匀空间的数据插 值更快。 i n t e r p 2 ( X , Y , Z , X x , 进行矩阵X x和Y y的二维插值,并由X、Y和Z Y y ) 所描述的函数Z=f(X,Y)内的插值所决定。如果X、 Y和Z中任何一个是一个向量,则它的元素被认 为应用于相应的行和列。 i n t e r p 2 ( X , Y , Z , X x , 进行二维插值,字符串m e t s t r规定了不同的插 Y y,m e t s t r ) 值方法,可用的方法有: ‘l i n e a r’ 线性插值。 ‘n e a r e s t’ 最邻近插值。 ‘s p l i n e’ 三次样条插值。 ‘c u b i c’ 三次插值。 V V = i n t e r p 3 ( X , Y , Z , 进行由X,Y和Z所描述的函数V的插值,X X、 V , X X , Y Y , Z Z , Y Y和Z Z是插值点。字符串m e t s t r规定了不同 m e t s t r ) 的插值方法,可用的方法有: ‘n e a r e s t’ 使用最邻近点的值。 ‘l i n e a r’ 使用8个最邻近点进行线性插值。 ‘s p l i n e’ 三次样条插值。 ‘c u b i c’ 使用6 4个最邻近点进行三次插值。 V V = i n t e r p n ( X 1 , X 2 , 和i n t e r p 3相同,但是V和V V可以是多维数组。 X 3,. . ., V , Y 1 ,,Y 2 , 如果X1,X2,X3,.. .是等距离的,使用星号*如 Y 3 ,. . ., m e t h o d ) ’ * c u b i c ’ 可以加快计算速度。 I n t e r p f t ( y , n ) 快速傅利叶变换插值,返回一个长度为n,从y计 算得到的向量。要求 y的值是等距离的,结果在 与y相同区间内计算。 g r i d d a t a ( x , y , z , 返回相同大小的矩阵X x和Y y,它们表示一个网 X x , Y y ,’m e t h o d’) 格,由函数z=f(x, y)的插值得到。向量 x、y和z 包含的是三维空间的 x 、y和z坐标。字符串 m e t h o d规定了不同的插值方法,可用的方法如 下: ‘l i n e a r’ 基于三角的线性插值。 ‘n e a r e s t’ 最邻近插值。 1 4 4 M ATLAB 5 手册 下载