
China-pub.com 下载 附录B线性代数中的定义和基本概念 这是对线性代数和矩阵代数基础的一个概要,MATLAB中也包含了用到的所有概念。 B.1向量 线性空间由可以进行加和数乘运算的向量组成。 线性空间R由列向量组成: X1 X2 2 y= : 其中,元素x和y为实数,长度为n。 在线性空间C中,元素可以为复数。 加法的定义是各元素分别相加: x1十y1 x2+2 x十y= xt十yn 数乘定义为各元素分别与数α相乘: 0x1 0x2 所有元素均为零的向量定义为零向量。 0 0 0 在线性空间的p个向量中,即x,x,…x的集合,如果至少有一个向量可以由其他向量 线性表示,则称这p个向量是线性相关的。 xp=a1X1十…+p-1xp-1 这里a为标量。 如果不能这样表示,则称这些向量线性无关。线性无关最通常的定义是:αx+α,x+… +a,x,=0成立,当且仅当a=0,==a,=0。 ■例B.1 向量
下载 附录B 线性代数中的定义和基本概念 这是对线性代数和矩阵代数基础的一个概要, M AT L A B中也包含了用到的所有概念。 B.1 向量 线性空间由可以进行加和数乘运算的向量组成。 线性空间R n由列向量组成: 其中,元素xk和yk为实数,长度为n。 在线性空间C n中,元素可以为复数。 加法的定义是各元素分别相加: 数乘定义为各元素分别与数a相乘: 所有元素均为零的向量定义为零向量。 在线性空间的p个向量中,即x1 , x2 , ……xp的集合,如果至少有一个向量可以由其他向量 线性表示,则称这p个向量是线性相关的。 这里ai为标量。 如果不能这样表示,则称这些向量线性无关。线性无关最通常的定义是: a1 x1 +a2 x2 +…… +ap xp = 0成立,当且仅当a1 =a2 =……=ap = 0。 ■ 例B . 1 向量

China-pub.com 附录B线性代数中的定义和基本概念 361 下载 =(Θ-(Θ-() 在线性空间R中是线性无关的。 ■ 线性空间中线性无关向量的最大个数称为线性空间的维数。R和C的维数均为。注意: 在有些情况下认为C"是2维的更为方便,这样就能分成实部和虚部两部分。 线性空间的基指的是一些向量的集合,这个空间中所有的向量都能由这些向量线性表示。 基中向量的个数等于空间的维数。线性空间中有无穷多组基。 ■例B.2 在例B.1中的向量形成R和C3空间中的基。向量: 0 0 0 形成同样空间中更常用的基,有: X2 =x1e1+x2e2+x3e3 这是R空间中一个由基向量线性表示的任意向量。可用图B-1来表示说明。 图B-1向量和它的分量 ■ C中两个向量x和y的内积或点积,通常写作(x,y)或,定义为: (x,y)= 如果严格限在R空间中,则x的复数共轭将是不必要的。可以使用下一节将要介绍的符号, (x,y)=xy。 C中向量的欧几里德范数xl,定义为: 川x3=(区,x)= ∑xP=xx i= 范数用来度量向量的大小或长度。还有许多其他范数,将在B.6节中介绍其中的一些范数。 如果(X,y)=0,则称两个向量x和y正交。 两个向量x和y之间的角度0是按下式来定义的: cos= (,y) x2yl2
在线性空间R n中是线性无关的。 线性空间中线性无关向量的最大个数称为线性空间的维数。 R n和C n的维数均为n。注意: 在有些情况下认为C n是2n维的更为方便,这样就能分成实部和虚部两部分。 线性空间的基指的是一些向量的集合,这个空间中所有的向量都能由这些向量线性表示。 基中向量的个数等于空间的维数。线性空间中有无穷多组基。 ■ 例B . 2 在例B . 1中的向量形成R 3和C 3空间中的基。向量: 形成同样空间中更常用的基,有: 这是R 3空间中一个由基向量线性表示的任意向量。可用图 B - 1来表示说明。 图B-1 向量和它的分量 Cn中两个向量x和y的内积或点积,通常写作(x, y)或,定义为: 如果严格限在Rn空间中,则xi的复数共轭将是不必要的。可以使用下一节将要介绍的符号, (x, y) =x Hy。 Cn中向量的欧几里德范数| |x| |2定义为: 范数用来度量向量的大小或长度。还有许多其他范数,将在 B . 6节中介绍其中的一些范数。 如果(x, y) = 0,则称两个向量x和y正交。 两个向量x和y之间的角度 是按下式来定义的: 附录B 线性代数中的定义和基本概念 3 6 1 下载 ■ ■

362 MATLAB5手册 China-pub.com 下载 已经知道两个正交向量之间的夹角是π/2或90度,即两个向量是垂直的。零向量与任何向 量都正交。 如果非零向量集合x,X,,x中所有向量都正交,则它们构成正交系,其中的向量也是 线性无关的。因此,正交化比线性无关的条件更强。如果X,x,“,x形成一个正交系,并且 每个向量的欧氏范数均为1,则称为标准正交系。标准正交系中的向量有如下关系: 0j≠k (区j,X) 1 j=k ■例B.3 例B2中的向量e,e,e,构成R(和C)中的标准正交系。在标准的笛卡儿坐标系中,它们分 别代表x,y,z轴。 ■ 除了以列向量的形式定义外,还可以以行向量的形式定义上述所有概念。 V=(U1,2,·,vp) 但是,使用列向量有几个优点。 B.2矩阵介绍 矩阵是一个以行列形式排列的数字矩形数组。一个有m行n列的矩阵称为m×n矩阵。例如, 这里有一个2×3矩阵: (32)=( 11 a12a13 a22 a23 矩阵中的数字称为矩阵的元素或分量。如果矩阵命名为A,矩阵A的元素称为α,这里代 表行下标,代表列下标,即α代表行列的元素。 n×n矩阵称为方阵。 矩阵的大小由行数m和列数n给出。对于方阵来说,n有时也指矩阵的阶数。 矩阵中从左上角到右下角的对角线称为主对角线,主对角线上的元素称为对角元素,。从 右上角到左下角的对角线称为反对角线。主对角线上方和下方的对角线分别称为上对角线和 下对角线。 大小相同的两个矩阵相加定义为矩阵的各个元素分别相加。矩阵C=A+B,也就是元素c, at b 数乘的定义也是每个元素分别相乘。矩阵oaA的元素为aa。 矩阵乘法仅在左侧矩阵的列数等于右侧矩阵的行数时才有意义。矩阵C=AB是一个m×n 矩阵,这里A为mXp矩阵,B为pXn矩阵。 k=] 元素c为A中行和B中j列的内积。 即使AB有意义,但BA不一定有意义。如果A和B都是n阶方阵,那么AB和BA将都有意义, 但是通常AB≠BA。矩阵乘法是不可交换的。 n阶单位矩阵是一个n×n矩阵,其中除对角线上元素为1外,其余元素均为0,用I或I表示。 A矩阵乘单位矩阵,结果不变,因此有IA=A和AI=A
已经知道两个正交向量之间的夹角是 p/ 2或9 0度,即两个向量是垂直的。零向量与任何向 量都正交。 如果非零向量集合 x1 , x2 , …, xp中所有向量都正交,则它们构成正交系,其中的向量也是 线性无关的。因此,正交化比线性无关的条件更强。如果 x1 , x2 , …, xp形成一个正交系,并且 每个向量的欧氏范数均为1,则称为标准正交系。标准正交系中的向量有如下关系: ■ 例B . 3 例B . 2中的向量e1 , e2 , e3构成Rn (和Cn )中的标准正交系。在标准的笛卡儿坐标系中,它们分 别代表x, y, z轴。 除了以列向量的形式定义外,还可以以行向量的形式定义上述所有概念。 但是,使用列向量有几个优点。 B.2 矩阵介绍 矩阵是一个以行列形式排列的数字矩形数组。一个有 m行n列的矩阵称为m×n矩阵。例如, 这里有一个2×3矩阵: 矩阵中的数字称为矩阵的元素或分量。如果矩阵命名为 A,矩阵A的元素称为ai j,这里i代 表行下标,j代表列下标,即ai j代表i行j列的元素。 n×n矩阵称为方阵。 矩阵的大小由行数m和列数n给出。对于方阵来说,n有时也指矩阵的阶数。 矩阵中从左上角到右下角的对角线称为主对角线,主对角线上的元素称为对角元素 ai i。从 右上角到左下角的对角线称为反对角线。主对角线上方和下方的对角线分别称为上对角线和 下对角线。 大小相同的两个矩阵相加定义为矩阵的各个元素分别相加。矩阵 C=A+B,也就是元素ci j = ai j + bi j。 数乘的定义也是每个元素分别相乘。矩阵 aA的元素为aai j。 矩阵乘法仅在左侧矩阵的列数等于右侧矩阵的行数时才有意义。矩阵 C=A B是一个m×n 矩阵,这里A为m×p矩阵,B为p×n矩阵。 元素ci j为A中i行和B中j列的内积。 即使A B有意义,但B A不一定有意义。如果A和B都是n阶方阵,那么A B和B A将都有意义, 但是通常A B≠B A。矩阵乘法是不可交换的。 n阶单位矩阵是一个n×n矩阵,其中除对角线上元素为1外,其余元素均为0,用I或I n表示。 A矩阵乘单位矩阵,结果不变,因此有 I A=A和A I=A。 3 6 2 M ATLAB 5 手册 下载 ■

China-pub.com 附录B线性代数中的定义和基本概念 363 下载 列向量可看成是n×1矩阵,而行向量可看成是1×n矩阵。有时将一个标量看成1×1矩阵 也是十分有用的。 如果x是一个有n个分量的列向量,而A是一个n×n阶矩阵,那么Ax也是有n个分量的列向 量。这称为矩阵一向量乘法。 转置是将矩阵的行和列交换位置,转置运算符记做T。如果A是一个元素为a的m×n矩阵, 那么转置矩阵A是一个元素为a的n×m矩阵。转置也可以看成是这样:A的第1列作为转置矩 阵中的第1行,A的第2列作为转置矩阵中的第2行,依次类推。 矩阵的共轭是一个矩阵,其中的元素是原矩阵中复数元素的共轭。结果记做A。一个常 用的操作符是共轭转置,这将形成矩阵AT或等价的AT。该矩阵通常记做A“,A*,在 MATLAB中记做A'。 两个列向量x和y的内积常写成: (x,y)= i=l 欧氏范数可写成风,=西。注意:xy是一个标量,因为它是1×n阶矩阵和n1阶矩阵的 内积。相反,xy是一个n×n阶矩阵。 B.3矩阵概念 矩阵不只是一个数字的集合。一些重要而有用的数学概念都与矩阵有关。 矩阵A的秩,rank(A)是矩阵A中线性无关列的列数,并且总是等于矩阵A中线性无关行的 行数。如果A为m×n矩阵,则秩小于或等于min(m,n)。 方阵A的行列式,dt(A),是一个可以用不同方式定义和计算的标量。有下列结论: 1)det(A)=det(AT). 2)det(A)=det(A). 3)如果A中有两行相等,或某一行可由其他行线性表示,则dt(A)=0。对于A的列也有同 样的结论。 4)某行减去另一行与一个标量的乘积,行列式不变。对于列也有同样的结论。 5)交换任意两行,行列式变号。对于列也有同样的结论。 6)主对角线下方所有元素均为零的矩阵称为上三角矩阵,其行列式为主对角元素的乘积。 对于下三角矩阵也有同样的结论。 7)矩阵乘积的行列式等于行列式的乘积。这是一个重要的乘法定理: det(AB)= det(A)det(B). 8)矩阵行列式的计算可用高斯消元法来很好地求得。 阶线性方程组可以记成如下明确的形式: a11x1+a12x2+...+aInxn=b1 a21x1+a22x2+··+a2nxn=b2 anlx1 a2nx2+...+annxn =bn 或用A=(a,,x=(,,…,x)和b=(b,bn…,b)来表示:
列向量可看成是 n×1矩阵,而行向量可看成是 1×n矩阵。有时将一个标量看成 1×1矩阵 也是十分有用的。 如果x是一个有n个分量的列向量,而 A是一个n×n阶矩阵,那么A x也是有n个分量的列向 量。这称为矩阵—向量乘法。 转置是将矩阵的行和列交换位置,转置运算符记做 T。如果A是一个元素为ai j的m×n矩阵, 那么转置矩阵AT是一个元素为aj i的n×m矩阵。转置也可以看成是这样: A的第1列作为转置矩 阵中的第1行,A的第2列作为转置矩阵中的第2行,依次类推。 矩阵的共轭是一个矩阵,其中的元素是原矩阵中复数元素的共轭。结果记做 。一个常 用的操作符是共轭转置,这将形成矩阵 或等价的 。该矩阵通常记做 AH,A*,在 M AT L A B中记做A¢。 两个列向量x和y的内积常写成: 欧氏范数可写成 。注意:x Hy是一个标量,因为它是 1×n阶矩阵和n×1阶矩阵的 内积。相反,x yH是一个n×n阶矩阵。 B.3 矩阵概念 矩阵不只是一个数字的集合。一些重要而有用的数学概念都与矩阵有关。 矩阵A的秩,r a n k(A)是矩阵A中线性无关列的列数,并且总是等于矩阵 A中线性无关行的 行数。如果A为m×n矩阵,则秩小于或等于m i n (m, n)。 方阵A的行列式,d e t ( A ),是一个可以用不同方式定义和计算的标量。有下列结论: 3) 如果A中有两行相等,或某一行可由其他行线性表示,则 d e t (A) = 0。对于A的列也有同 样的结论。 4) 某行减去另一行与一个标量的乘积,行列式不变。对于列也有同样的结论。 5) 交换任意两行,行列式变号。对于列也有同样的结论。 6) 主对角线下方所有元素均为零的矩阵称为上三角矩阵,其行列式为主对角元素的乘积。 对于下三角矩阵也有同样的结论。 7) 矩阵乘积的行列式等于行列式的乘积。这是一个重要的乘法定理: d e t (A B) = d e t (A) d e t (B)。 8) 矩阵行列式的计算可用高斯消元法来很好地求得。 n阶线性方程组可以记成如下明确的形式: 或用A= (ai j ),x= (x1 , x2 , …,xn ) T和b= (b1 , b2 ,…,bn ) T来表示: x 2 = x H x 附录B 线性代数中的定义和基本概念 3 6 3 下载

364 MATLAB5手册 China-pub.com 下载 Ax=b 将向量a,a,,a看作A的列,该方程组可被写成如下的半压缩形式。 x1a1+x2a2+…+xnan=b 当且仅当det(A)≠O时方程组有唯一解。 mXn阶矩阵A的值域R(A)是A的列a,a,,a的所有线性的组合。这是一个线性空间, 并且R(A)的维数等于rank(A)。 矩阵A的零空间N(A)是所有使得Ax=0的向量集合,即齐次方程组的解。这也是一个线性 空间,并且维数等于m一rank(A)。 A的值域和零空间的定义同上。 方程系AX-I是一个矩阵方程,其中A是一个nXn矩阵,而I为n阶单位阵。使用符号x,x, …,,x和e=(1,0,…,0)',e=(0,1,…,0),…,e=(0,0,…,1)作为X和I的列,根据: X=(x1 x2 ..Xn)I=(el e2 ..en) 可以将矩阵方程写成线性方程组的集合: Axk=ek k=1,2,....n 当且仅当det(A)≠0时方程组有唯一的解。AX=I的解X被称为A的逆,记为A-, 有AA1=I和A1A=I。 逆的计算通常也使用高斯消元法。存在逆的矩阵称为非奇异矩阵,否则称为奇异矩阵。 方阵的特征值和特征向量可用如下的方程定义: Ax=Ix 这等价于齐次方程组: (A-1ID)x=0 对于每个矩阵A和入,向量x=0都是一个解。但是,如果dt(A一2I)≠0,则方程组还有非 零解。这些×≠0的解称为A的特征向量,相应的入,称为特征值或特征根。在复平面上A总有 个特征值入,入,,入。特征值和它相应的特征向量称为特征对。 函数p(仉)=det(A-入I)是入的n次多项式,也称为A的特征多项式。特征方程为p(久)=0。 总有这样的结论:矩阵多项式p(A)=O,这就是Cayley-Hamilton定理。 如果C为非奇异矩阵,A和B定义成B=C-AC,则称A和B为相似矩阵,A和B之间的变换 称为相似变换。相似变换不改变矩阵的特征值。 矩阵A的谱半径p(A)定义为max。 如果矩阵A、B的逆存在,则对逆、转置和共轭转置如下的式子成立: (AB)-I=B-1A-1如果所有的逆都存在 (AB)T =BTAT (AB)H BHAH 下面的等价链包含了上述的大部分定义。A为n阶方阵。 线性方程Ax=b有唯一的解 台 det(A≠0 台
A x = b 将向量a1 , a2 ,…,an看作A的列,该方程组可被写成如下的半压缩形式。 当且仅当d e t (A)≠0时方程组有唯一解。 m×n阶矩阵A的值域 (A)是A的列a1 , a2 ,…,an的所有线性的组合。这是一个线性空间, 并且 (A)的维数等于r a n k(A)。 矩阵A的零空间 (A)是所有使得A x = 0的向量集合,即齐次方程组的解。这也是一个线性 空间,并且维数等于m—r a n k(A)。 AT的值域和零空间的定义同上。 方程系A X = I是一个矩阵方程,其中 A是一个n×n矩阵,而I为n阶单位阵。使用符号 x1 , x2 , …,xn和e1 =(1, 0, …,0 ) T , e2 =(0, 1, …,0) T , …,en =(0, 0, …,1) T作为X和I的列,根据: 可以将矩阵方程写成线性方程组的集合: 当且仅当d e t (A) ¹ 0时方程组有唯一的解。A X = I的解X被称为A的逆,记为A-1 , 有A A-1=I和A-1A = I。 逆的计算通常也使用高斯消元法。存在逆的矩阵称为非奇异矩阵,否则称为奇异矩阵。 方阵的特征值和特征向量可用如下的方程定义: A x = l x 这等价于齐次方程组: (A-lI)x= 0 对于每个矩阵A和l,向量x = 0都是一个解。但是,如果 d e t (A-lI)≠0,则方程组还有非 零解。这些xk≠0的解称为A的特征向量,相应的 lk称为特征值或特征根。在复平面上 A总有n 个特征值l1 , l2 ,…,ln。特征值和它相应的特征向量称为特征对。 函数j(l) = d e t (A-lI )是l的n次多项式,也称为A的特征多项式。特征方程为 j(l) = 0。 总有这样的结论:矩阵多项式 (A) = 0,这就是C a y l e y - H a m i l t o n定理。 如果C为非奇异矩阵,A和B定义成B= C-1A C,则称A和B为相似矩阵,A和B之间的变换 称为相似变换。相似变换不改变矩阵的特征值。 矩阵A的谱半径r(A)定义为m a xi |li |。 如果矩阵A、B的逆存在,则对逆、转置和共轭转置如下的式子成立: 下面的等价链包含了上述的大部分定义。 A为n阶方阵。 3 6 4 M ATLAB 5 手册 下载 如果所有的逆都存在 线性方程A x=b有唯一的解 Û d e t ( A ¹ 0 Û

China-pub.com 附录B线性代数中的定义和基本概念 365 下载 A存在 台 A的秩为n 台 A的列线性无关 台 A的行线性无关 台 A的值域维数为n 台 A的零空间维数为0 台 齐次方程组Ax=0有唯一的零解 台 =0不是A的特征值 台 B.4矩阵分类 矩阵可用多种方式分类。一个矩阵中如果所有非对角元素均为零,则称为对角阵。如果 所有主对角线下方的元素均为0,则称为上三角阵,如果对角线上的元素也都为零,则称为严 格上三角阵。同样,也可以定义下三角阵和严格下三角阵。 如果仅在主对角线、第一条上对角线和第一条下对角线上有非零元素,则称矩阵为三对 角矩阵。更一般的是,如果所有非零元素均在主对角线周围的带形区域内,则称为带状矩阵。 如果第一条子对角线下方的元素均为零,则称为上海森伯格形式。 如果矩阵中大部分元素都是零,称为稀疏矩阵:否则,称为满矩阵。带状矩阵属于稀疏矩阵。 使用分块矩阵也是十分有用的,分块矩阵即矩阵的元素也是矩阵。实际上代数运算不变。 假设A,B的定义如下: A= A11A12 A21 B= B11B12 A22 B21B22 可给出C=AB: C= C11C12 C21C22 其中,比如:C,=AB+AB2 块矩阵有时也称为分区矩阵。在前面的例子中,子矩阵的大小必须一致。类似块对角阵, 块上三角阵的定义就不再赘述了。 矩阵还可以按数学性质分类。已介绍过的一些概念,这里再重复一下。 如果det(A)≠0,则称矩阵A为非奇异矩阵,这意味着所有的特征值都是非零值。如果
B.4 矩阵分类 矩阵可用多种方式分类。一个矩阵中如果所有非对角元素均为零,则称为对角阵。如果 所有主对角线下方的元素均为 0,则称为上三角阵,如果对角线上的元素也都为零,则称为严 格上三角阵。同样,也可以定义下三角阵和严格下三角阵。 如果仅在主对角线、第一条上对角线和第一条下对角线上有非零元素,则称矩阵为三对 角矩阵。更一般的是,如果所有非零元素均在主对角线周围的带形区域内,则称为带状矩阵。 如果第一条子对角线下方的元素均为零,则称为上海森伯格形式。 如果矩阵中大部分元素都是零,称为稀疏矩阵;否则,称为满矩阵。带状矩阵属于稀疏矩阵。 使用分块矩阵也是十分有用的,分块矩阵即矩阵的元素也是矩阵。实际上代数运算不变。 假设A,B的定义如下: 可给出C = A B: 其中,比如:C11= A11 B11+A1 2B21。 块矩阵有时也称为分区矩阵。在前面的例子中,子矩阵的大小必须一致。类似块对角阵, 块上三角阵的定义就不再赘述了。 矩阵还可以按数学性质分类。已介绍过的一些概念,这里再重复一下。 如果d e t ( A )≠0,则称矩阵 A为非奇异矩阵,这意味着所有的特征值都是非零值。如果 附录B 线性代数中的定义和基本概念 3 6 5 A-1存在 Û A的秩为n Û A的列线性无关 Û A的行线性无关 Û A的值域维数为n Û A的零空间维数为0 Û 齐次方程组A x = 0有唯一的零解 Û l= 0不是A的特征值 Û 下载

366 MATLAB5手册 China-bub.com 下载 det(A)=0,矩阵为奇异矩阵,至少有一个特征值为零。 如果A“=A,矩阵A为Hermitian矩阵。这与实数阵的对称矩阵类似。特征值为实数,特征 向量形成一个标准正交基。 如果A=一A,矩阵A为反Hermitian矩阵。这与实数阵的反对称矩阵类似。特征值为虚数, 特征向量形成一个标准正交基。 如果A“A=AA“,则称A为标准阵。特征向量形成标准正交基。 如果AA=,则称A为酉矩阵。这类似于实数矩阵的正交阵。由此得A=A“。A的列形成 标准正交基,行也一样。特征值一定为1,特征向量形成标准正交基。 如果对每个x≠0,都有x"Ax>0,则称Hermitian?矩阵为正定的。所有特征值均为正数。 用同样的方式可以对较弱的条件x“Ax≥0定义半正定矩阵,特征值均为非负。 对于某个整数P,如果A-0,则称矩阵A为幂零矩阵。如果A2=A,则称矩阵A为幂等矩阵。 如果存在相似变换C,使得C-AC为对角阵,则称A是可对角化的。A可对角化当且仅当 A有n个线性无关的特征向量。 B.5特殊矩阵 所有元素均为零的矩阵称为零矩阵。所有元素均为1的矩阵称为1矩阵。单位矩阵主对角 线上元素均为1,其他元素均为零。随机矩阵的元素都是随机的。 Givens旋转是具有如下形式的矩阵: 与单位阵的区别仅在(i,).(i,),U,)和Uj)四处。Givensh旋转是正交的。 cos0 sin -sinθcos0 Householder反射是由I一2wHw定义的矩阵,其中wHw=l。这些矩阵是酉矩阵和Hermitian 矩阵。 高斯变换矩阵有如下的形式: 1 其中×代表非零元素。它仅在对角线下方的一列上与单位阵有区别
d e t ( A ) = 0,矩阵为奇异矩阵,至少有一个特征值为零。 如果AH=A,矩阵A为H e r m i t i a n矩阵。这与实数阵的对称矩阵类似。特征值为实数,特征 向量形成一个标准正交基。 如果AH=-A,矩阵A为反H e r m i t i a n矩阵。这与实数阵的反对称矩阵类似。特征值为虚数, 特征向量形成一个标准正交基。 如果AH A=A AH,则称A为标准阵。特征向量形成标准正交基。 如果AHA= I,则称A为酉矩阵。这类似于实数矩阵的正交阵。由此得 A-1= AH。A的列形成 标准正交基,行也一样。特征值一定为 1,特征向量形成标准正交基。 如果对每个x≠0,都有x HA x > 0,则称H e r m i t i a n矩阵为正定的。所有特征值均为正数。 用同样的方式可以对较弱的条件 x H A x≥0定义半正定矩阵,特征值均为非负。 对于某个整数p,如果Ap= 0,则称矩阵A为幂零矩阵。如果A2=A,则称矩阵A为幂等矩阵。 如果存在相似变换 C,使得C-1A C为对角阵,则称 A是可对角化的。 A可对角化当且仅当 A有n个线性无关的特征向量。 B.5 特殊矩阵 所有元素均为零的矩阵称为零矩阵。所有元素均为 1的矩阵称为1矩阵。单位矩阵主对角 线上元素均为1,其他元素均为零。随机矩阵的元素都是随机的。 G i v e n s旋转是具有如下形式的矩阵: 与单位阵的区别仅在(i,i) , (i, j), (j, i)和(j j)四处。G i v e n s旋转是正交的。 H o u s e h o l d e r反射是由I-2 wH w定义的矩阵,其中wH w = 1。这些矩阵是酉矩阵和H e r m i t i a n 矩阵。 高斯变换矩阵有如下的形式: 其中×代表非零元素。它仅在对角线下方的一列上与单位阵有区别。 3 6 6 M ATLAB 5 手册 下载

China-pub.com 附录B线性代数中的定义和基本概念 367 下载 置换矩阵与单位矩阵有相同的列,但是次序不同。每行每列都有一个准确的单位元素。 B.61 向量和矩阵的范数 前面已经介绍了向量x的欧氏范数或2-范数。 x:2=√xHx 介绍最大范数也是十分有用的。 lllo= 另一个范数是1-范数。 I1=2x i=1 所有这些都是更一般的p-范数的特例。 范数常用来度量向量的大小或长度。 矩阵范数用下式来定义: AxIl lAll max =max Axll x≠0‖x‖x台1 可以得到下面的结论: ·A的1-范数是列和绝对值的最大值。 All1 max ∑lal ·A的2-范数或谱范数: IAl2=√p(AHA) 而A的最大范数是行元素绝对值之和的最大值。 IlAll oo max I≤i≤m 另一个常用的矩阵范数是F-范数Al,用下面的式子定义: Ia眼=∑∑E F-范数不能象另外三个矩阵范数那样由向量范数定义得到。 有下列不等式:
置换矩阵与单位矩阵有相同的列,但是次序不同。每行每列都有一个准确的单位元素。 B.6 向量和矩阵的范数 前面已经介绍了向量x的欧氏范数或2-范数。 介绍最大范数也是十分有用的。 另一个范数是1 -范数。 所有这些都是更一般的p-范数的特例。 范数常用来度量向量的大小或长度。 矩阵范数用下式来定义: 可以得到下面的结论: • A的1 -范数是列和绝对值的最大值。 • A的2 -范数或谱范数: 而A的最大范数是行元素绝对值之和的最大值。 另一个常用的矩阵范数是F-范数| |A| |F ,用下面的式子定义: F-范数不能象另外三个矩阵范数那样由向量范数定义得到。 有下列不等式: 附录B 线性代数中的定义和基本概念 3 6 7 下载

368 MATLAB5手册 China-pub.coM 下载 1)对任何矩阵A和它所有的范数,有p(A)≤A。 2)如果A为Hermitian?矩阵,则p(A)=Al,。 3)如果A为酉矩阵,则lAl=1。 使用矩阵范数可以对矩阵中扰动的灵敏性进行估计和度量。 线性方程组Ax=b的条件数定义为: cond(A)=IlAll IlAIl 有如下关系: lAy≤cond(A) llxi bl 其中,△b是对右侧b的扰动,而△x是对解向量x的相应的扰动。注意到关系中既有向量 范数又有矩阵范数。对矩阵A中的扰动也有类似的关系。 B.7矩阵因式分解 1)LU因式分解或LU分解PA=LU,其中P为扰动矩阵,L为一个对角线上有元素为1的下 三角矩阵,而U为一个上三角矩阵。 2)Cholesky因式分解对称、正定矩阵A可以因式分解为A=GG',这里G为下三角阵。 3)QR因式分解A=QR,其中A是m×n矩阵,Q是一个mXm的正交矩阵,而R是mXm的 上三角矩阵。 4)假设A有n个线性无关的特征向量,则存在矩阵C,使得C-AC=D为对角阵,即A= CDC-,该条件是充分必要的。一个充分条件是所有的特征值均不同。 5)舒尔分解对每个矩阵A,存在矩阵U,使得UAU=T为上三角阵,即A=UTU“。 6)对于Hermitian:矩阵A,存在一个酉矩阵U,使得UHAU-D为对角阵,即A=UTU"。 7)Murnaghan-Winters定理对于所有的实数阵A,存在实数正交阵U,使得U'AU=B为 实数分块三角阵,这里对角线上的块为2×2阶或1×1阶。每个2阶块代表一个特征值的复数共 轭对。 8)Jordan标准形对每一个方阵A,存在一个非奇异矩阵S,使得SAS-J,其中J为块对 角阵的形式: 如果块J为一阶,则J=(?,)。与对角线上的每一个块相对应的一个特征向量也称为Jordan 框。如果Jordan框的数日为p,则矩阵A有p个线性无关的特征向量。 9)奇异值分解每个mXn矩阵A都可分解成两个酉矩阵U和V,使得U'AV=D是一个m×n 对角阵。其中,U是一个m×m矩阵,V是一个n×n矩阵,而D的对角元素为o,。这些元素有序 排列为o,≥o,≥.o≥0,其中,p≤min(m,n)。如果有其他的o,则为零。o的值称为A的奇 异值。因此A=UDV
1) 对任何矩阵A和它所有的范数,有 (A)≤| |A| |。 2) 如果A为H e r m i t i a n矩阵,则 (A) = | |A| |2。 3) 如果A为酉矩阵,则| |A| |2 = 1。 使用矩阵范数可以对矩阵中扰动的灵敏性进行估计和度量。 线性方程组A x = b的条件数定义为: 有如下关系: 其中,△b是对右侧b的扰动,而△x是对解向量x的相应的扰动。注意到关系中既有向量 范数又有矩阵范数。对矩阵 A中的扰动也有类似的关系。 B.7 矩阵因式分解 1) L U因式分解或L U分解 PA = L U,其中P为扰动矩阵,L为一个对角线上有元素为1的下 三角矩阵,而U为一个上三角矩阵。 2) C h o l e s k y因式分解 对称、正定矩阵A可以因式分解为A = G GT,这里G为下三角阵。 3) Q R因式分解 A = Q R,其中A是m×n矩阵,Q是一个m×m的正交矩阵,而R是m×m的 上三角矩阵。 4 ) 假设A有n个线性无关的特征向量,则存在矩阵 C,使得 C-1A C = D为对角阵,即 A= C D C-1,该条件是充分必要的。一个充分条件是所有的特征值均不同。 5) 舒尔分解 对每个矩阵A,存在矩阵U,使得UHA U=T为上三角阵,即A = U T UH。 6) 对于H e r m i t i a n矩阵A,存在一个酉矩阵U,使得UHA U = D为对角阵,即A = U T UH。 7) M u r n a g h a n - Wi n t e r s定理 对于所有的实数阵A,存在实数正交阵U,使得UTA U=B为 实数分块三角阵,这里对角线上的块为 2×2阶或1×1阶。每个2阶块代表一个特征值的复数共 轭对。 8) J o r d a n标准形 对每一个方阵A,存在一个非奇异矩阵S,使得S - 1A S = J,其中J为块对 角阵的形式: 如果块J k为一阶,则Jk = (lk )。与对角线上的每一个块相对应的一个特征向量也称为 J o r d a n 框。如果J o r d a n框的数目为p,则矩阵A有p个线性无关的特征向量。 9) 奇异值分解 每个m×n矩阵A都可分解成两个酉矩阵U和V,使得UTAV = D是一个m×n 对角阵。其中, U是一个m×m矩阵, V是一个n×n矩阵,而D的对角元素为sk。这些元素有序 排列为s1≥s2≥. . .sp≥0,其中,p≤m i n (m, n)。如果有其他的 sk,则为零。sk的值称为A的奇 异值。因此A = U D VT。 3 6 8 M ATLAB 5 手册 下载
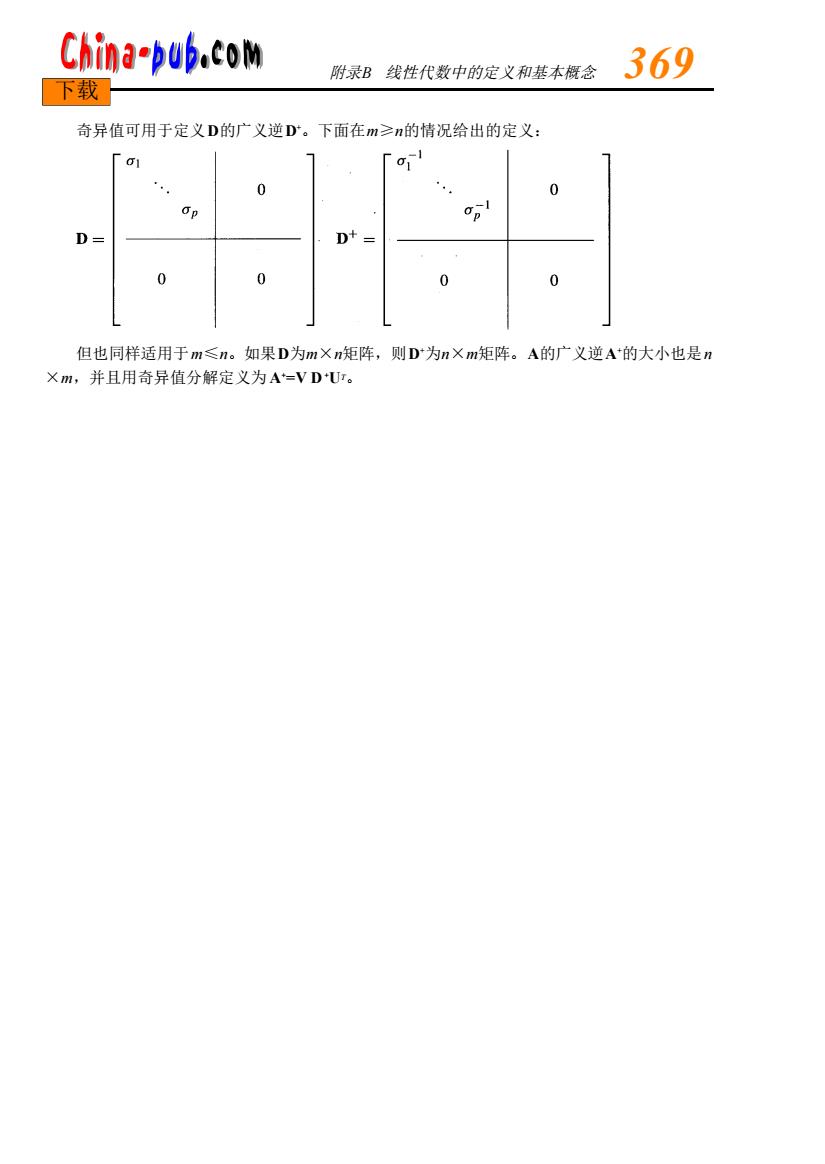
China-bub.coM 附录B线性代数中的定义和基本概念 369 下载 奇异值可用于定义D的广义逆D。下面在m≥n的情况给出的定义: 0 D= D+= 0 0 0 0 但也同样适用于m≤n。如果D为mXn矩阵,则D为nXm矩阵。A的广义逆A的大小也是n Xm,并且用奇异值分解定义为A-VDUr
奇异值可用于定义D的广义逆D+。下面在m≥n的情况给出的定义: 但也同样适用于m≤n。如果D为m×n矩阵,则D+为n×m矩阵。A的广义逆A+的大小也是n ×m,并且用奇异值分解定义为 A+=V D+UT。 附录B 线性代数中的定义和基本概念 3 6 9 下载