
China-bub.com 下载 附录A MATLAB初步 这是一个MATLAB的简短介绍。建议在阅读本书的同时使用介绍的命令。若要详细地了 解有关命令,请参见每一节的内容和/或使用help或helpdesk。所有的命令见附录D和命令列表。 A.1启动和退出MATLAB 根据使用的计算机,单击图标或输入matlab就可以启动MATLAB。详细内容见2.1节。 以下信息出现在MATLAB的命令窗口中: MA T L AB (R)> (c)Copyright 1984-98 The MathWorks,Inc. All Rights Reserved Version 5.2.0.3084 Jan171998 To get started,type one of these:helpwin,helpdesk,or demo. For product information,type tour or visit www.mathworks.com. 使用这些命令是非常好的。命令tour和demo也是非常有实用价值的。在MATLAB提示 符后键入一个命令,当按下回车键后,就执行该命令。 >tour← 在本书的其他节将不给出MATLAB提示符,因为这将使读者阅读起来比较困难。命令应 在提示符>后键入,但提示符不在每一行中列出。 注意,本书使用不同的字体以区别用户在提示符处输入的命令和MATLAB返回的运行结 果。见1.2节。 退出MATLAB,只需输入quit并回车即可。从这以后将不强调在命令行后输入回车键。 >>quit 如果想要终止MATLAB的运行,就要同时按下‘CTRL’和‘c'键。MATLAB将停止其 运行的所有工作,并且在屏幕上给出提示符,等待输入。 >> A.2基本赋值和计算 通常,MATLAB能被当作计算器使用: 5011+13 ans 5024 同一行上可以有多条命令:
下载 附录A MAT L A B初步 这是一个M AT L A B的简短介绍。建议在阅读本书的同时使用介绍的命令。若要详细地了 解有关命令,请参见每一节的内容和 /或使用h e l p或h e l p d e s k。所有的命令见附录D和命令列表。 A.1 启动和退出M AT L A B 根据使用的计算机,单击图标或输入 m a t l a b就可以启动 M AT L A B。详细内容见 2 . 1节。 以下信息出现在M AT L A B的命令窗口中: 使用这些命令是非常好的。命令 t o u r和d e m o也是非常有实用价值的。在 M AT L A B提示 符后键入一个命令,当按下回车键后,就执行该命令。 在本书的其他节将不给出 M AT L A B提示符,因为这将使读者阅读起来比较困难。命令应 在提示符> >后键入,但提示符不在每一行中列出。 注意,本书使用不同的字体以区别用户在提示符处输入的命令和 M AT L A B返回的运行结 果。见1 . 2节。 退出M AT L A B,只需输入q u i t并回车即可。从这以后将不强调在命令行后输入回车键。 > > q u i t 如果想要终止M AT L A B的运行,就要同时按下‘ C T R L’和‘c’键。M AT L A B将停止其 运行的所有工作,并且在屏幕上给出提示符,等待输入。 > > A.2 基本赋值和计算 通常,M AT L A B能被当作计算器使用: 同一行上可以有多条命令:

348 MATLAB5手册 China-pub.com 下载 2^5,2*(3+2) ans 32 ans 10 通常,变量用于保存所赋的值和结果。如果没有赋值,MATLAB将结果存放在名为ans的 变量中。现在定义变量并赋值: x=14 X 14 多三3*x 42 所有的基本数学函数在MATLAB中有定义(见2.4节): sin(x) ans 0.9906 圆括号’0',可在数学式子中使用。 u=2*x-y; w=2*(x-y); exp(2-u)/(w-2) ans 0.7589 注意,在命令行尾的分号‘;’是MATLAB‘quietly'执行赋值命令,即在屏幕上不回显 信息,但计算照常执行。 MATLAB中的变量通常为向量或矩阵: vco1=[1;2;3;4],vrow=[5678] vcol 1 2 4 VrOw 5 6 7 8 A=[1234;5678;9101112]
通常,变量用于保存所赋的值和结果。如果没有赋值, M AT L A B将结果存放在名为a n s的 变量中。现在定义变量并赋值: 所有的基本数学函数在M AT L A B中有定义(见2 . 4节): 圆括号’( )’,可在数学式子中使用。 注意,在命令行尾的分号‘ ;’是M AT L A B‘q u i e t l y’执行赋值命令,即在屏幕上不回显 信息,但计算照常执行。 M AT L A B中的变量通常为向量或矩阵: 3 4 8 M ATLAB 5 手册 下载

China-bub.com 附录MATLAB初步 349 下载 A 1 4 5 6 7 9 10 11 12 注意,各行要用分号隔开。 在单个命令中,函数可用于向量或矩阵。 sqrt(vcol) ans 1.0000 1.4142 1.7321 2.0000 到现在为止,已经定义了许多变量。输入以下命令,可以得到变量列表: who Your variables are: u VrOW ans vcol 命令whos也将显示当前的变量,同时还显示出每个变量的其他信息。试使用这个命令, 并看看如何区别变量是标量还是向量。 MATLAB在程序运行过程中保存所有的变量,清除变量应输入: clear 先前的变量现在全被清除。此时,如果输入wo,将不会返回任何信息:见2.3节。向量 可通过使用元素操作运算符来生成:见4.3节。 vector =0:8 vector 0 1 2 3 456 7 8 vector2=0:0.5:2 vector2 0.5000 1.0000 1.50002.0000 命令linspace和logspace也可用来创建向量:见4.3节。通过使用双操作符向量也可 直接计算。 values =2.vector values 1 248163264128256 注意,先前使用的运算符八,表示应对向量中的每一个元素进行操作。见35节。 借助箭头键,能重复先前所给的命令:见21节。如果输入有误,它就能避免再写过长的
注意,各行要用分号隔开。 在单个命令中,函数可用于向量或矩阵。 到现在为止,已经定义了许多变量。输入以下命令,可以得到变量列表: 命令w h o s也将显示当前的变量,同时还显示出每个变量的其他信息。试使用这个命令, 并看看如何区别变量是标量还是向量。 M AT L A B在程序运行过程中保存所有的变量,清除变量应输入: C l e a r 先前的变量现在全被清除。此时,如果输入 w h o,将不会返回任何信息;见 2 . 3节。向量 可通过使用元素操作运算符来生成;见 4 . 3节。 命令l i n s p a c e和l o g s p a c e也可用来创建向量;见 4 . 3节。通过使用双操作符向量也可 直接计算。 注意,先前使用的运算符 ^,表示应对向量中的每一个元素进行操作。见 3 . 5节。 借助箭头键,能重复先前所给的命令;见 2 . 1节。如果输入有误,它就能避免再写过长的 附录A MAT L A B初步 3 4 9 下载
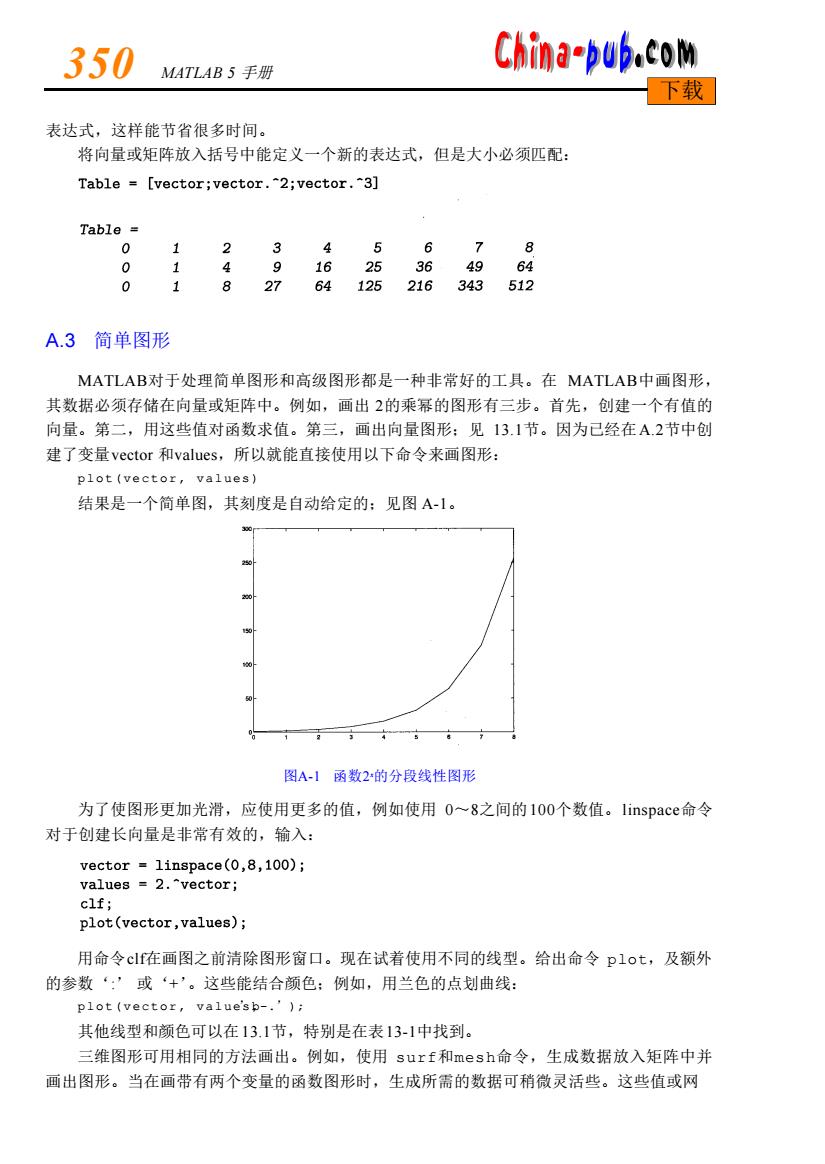
350 MATLAB5手册 China-pub.com 下载 表达式,这样能节省很多时间。 将向量或矩阵放入括号中能定义一个新的表达式,但是大小必须匹配: Table =[vector;vector.2;vector.3] Table 0 2 5 6 A 8 0 1 16 25 36 49 64 0 1 27 64 125 216 343 512 A.3 简单图形 MATLAB对于处理简单图形和高级图形都是一种非常好的工具。在MATLAB中画图形, 其数据必须存储在向量或矩阵中。例如,画出2的乘幂的图形有三步。首先,创建一个有值的 向量。第二,用这些值对函数求值。第三,画出向量图形:见131节。因为已经在A.2节中创 建了变量vector和values,所以就能直接使用以下命令来画图形: plot(vector,values) 结果是一个简单图,其刻度是自动给定的:见图A-1。 300 250 20 50 图A-1函数2的分段线性图形 为了使图形更加光滑,应使用更多的值,例如使用0~8之间的100个数值。linspace命令 对于创建长向量是非常有效的,输入: vector linspace(0,8,100); values =2.vector; clf; plot(vector,values); 用命令cf在画图之前清除图形窗口。现在试着使用不同的线型。给出命令p1ot,及额外 的参数‘:’或‘+’。这些能结合颜色:例如,用兰色的点划曲线: plot (vector,value'sb-.'); 其他线型和颜色可以在13.1节,特别是在表13-1中找到。 三维图形可用相同的方法画出。例如,使用surf和mesh命令,生成数据放入矩阵中并 画出图形。当在画带有两个变量的函数图形时,生成所需的数据可稍微灵活些。这些值或网
表达式,这样能节省很多时间。 将向量或矩阵放入括号中能定义一个新的表达式,但是大小必须匹配: A.3 简单图形 M AT L A B对于处理简单图形和高级图形都是一种非常好的工具。在 M AT L A B中画图形, 其数据必须存储在向量或矩阵中。例如,画出 2的乘幂的图形有三步。首先,创建一个有值的 向量。第二,用这些值对函数求值。第三,画出向量图形;见 1 3 . 1节。因为已经在A . 2节中创 建了变量vector 和v a l u e s,所以就能直接使用以下命令来画图形: plot(vector, values) 结果是一个简单图,其刻度是自动给定的;见图 A - 1。 图A-1 函数2 x的分段线性图形 为了使图形更加光滑,应使用更多的值,例如使用 0~8之间的1 0 0个数值。l i n s p a c e命令 对于创建长向量是非常有效的,输入: 用命令c l f在画图之前清除图形窗口。现在试着使用不同的线型。给出命令 p l o t,及额外 的参数‘:’ 或‘+’。这些能结合颜色;例如,用兰色的点划曲线: plot(vector, values, ’b - .’) ; 其他线型和颜色可以在1 3 . 1节,特别是在表1 3 - 1中找到。 三维图形可用相同的方法画出。例如,使用 s u r f和m e s h命令,生成数据放入矩阵中并 画出图形。当在画带有两个变量的函数图形时,生成所需的数据可稍微灵活些。这些值或网 3 5 0 M ATLAB 5 手册 下载
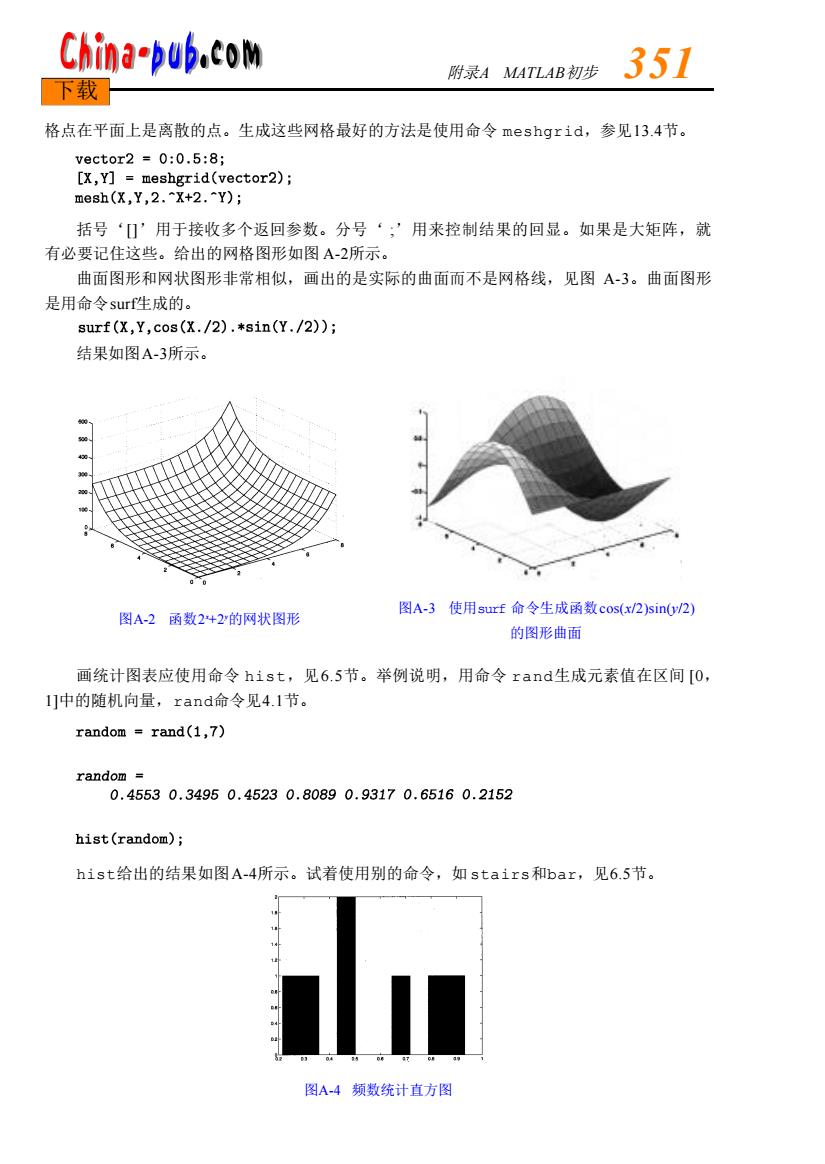
China-pub.coM 附录MATLAB初步 351 下载 格点在平面上是离散的点。生成这些网格最好的方法是使用命令meshgrid,参见13.4节。 vector2=0:0.5:8; [X,Y]meshgrid(vector2); mesh(X,Y,2.X+2.Y) 括号‘[’用于接收多个返回参数。分号‘,’用来控制结果的回显。如果是大矩阵,就 有必要记住这些。给出的网格图形如图A-2所示。 曲面图形和网状图形非常相似,画出的是实际的曲面而不是网格线,见图A-3。曲面图形 是用命令surf生成的。 surf(X,Y,cos(X./2)*sin(Y./2)); 结果如图A-3所示。 图A-2函数2+2的网状图形 图A-3使用surf命令生成函数cos(x/2)sin0/2) 的图形曲面 画统计图表应使用命令hist,见6.5节。举例说明,用命令rand生成元素值在区间[0, 1中的随机向量,rand命令见4.1节。 random rand(1,7) random 0.45530.34950.45230.80890.93170.65160.2152 hist(random); hist给出的结果如图A-4所示。试着使用别的命令,如stairs和bar,见6.5节。 图A-4频数统计直方图
格点在平面上是离散的点。生成这些网格最好的方法是使用命令 m e s h g r i d,参见1 3 . 4节。 括号‘[ ]’用于接收多个返回参数。分号‘ ;’用来控制结果的回显。如果是大矩阵,就 有必要记住这些。给出的网格图形如图 A - 2所示。 曲面图形和网状图形非常相似,画出的是实际的曲面而不是网格线,见图 A - 3。曲面图形 是用命令s u r f生成的。 结果如图A - 3所示。 画统计图表应使用命令 h i s t,见6 . 5节。举例说明,用命令 r a n d生成元素值在区间 [ 0, 1 ]中的随机向量,r a n d命令见4 . 1节。 h i s t给出的结果如图A - 4所示。试着使用别的命令,如 s t a i r s和b a r,见6 . 5节。 图A-4 频数统计直方图 附录A MAT L A B初步 3 5 1 下载 图A-2 函数2 x+ 2y的网状图形 图A-3 使用s u r f 命令生成函数c o s (x/ 2 ) s i n (y/ 2 ) 的图形曲面

352 MATLAB5手册 China-pub.com 下载 A.4 线性系统和矩阵特征值 定义矩阵: 3 4 5 2 2 23 B=(什7) 用下面的语句: A=[345;522;123]; B=[123;111]; 用命令B*A来做矩阵相乘,结果如下: ans 16 14 18 g 8 10 但是A*B的结果为: ??Error using ==> Inner matrix dimensions must agree. 因为这种矩阵的乘法没有定义,见32节。 计算A的行列式值,可使用命令det: det(A) ans -6 B的行列式值没有定义。也可试着对同一矩阵使用trace、null、orth和inv命令,这 些命令在7.1节有定义。 下面来看看线性方程组: 3x1+4x2+5x3=25 5x1+2x2+2x3=18 x1+2x2+3x3=13 或者是矩阵表达式Ax=b,A是上面定义的,b如下: 25 b= 18 13 可用反斜杠运算符‘\’来求解方程组。 b=[25;18;13]; A\b ans 2.0000 1.0000 3.0000 可以用同样的方法来解超定方程组。因为通常这些方程组没有真解,MATLAB用最小二
A.4 线性系统和矩阵特征值 定义矩阵: 用下面的语句: 用命令B * A来做矩阵相乘,结果如下: 但是A * B的结果为: 因为这种矩阵的乘法没有定义,见 3 . 2节。 计算A的行列式值,可使用命令d e t : B的行列式值没有定义。也可试着对同一矩阵使用 t r a c e、n u l l、o r t h和i n v命令,这 些命令在7 . 1节有定义。 下面来看看线性方程组: 或者是矩阵表达式A x=b,A是上面定义的,b如下: 可用反斜杠运算符‘\’来求解方程组。 可以用同样的方法来解超定方程组。因为通常这些方程组没有真解, M AT L A B用最小二 3 5 2 M ATLAB 5 手册 下载

China-bub.coM 附录A MATLAB初步 353 下载 乘法来解。见72和7.7节。 特征值和特征向量可由命令eig求得。例如,对上面的矩阵A求: [EigenVectors,EigenValues]eig(A) EigenVectors -0.7111-0.4501 -0.0210 -0.6185 0.8459 -0.7756 -0.3342 -0.2863 0.6309 EigenValues 8.8291 0 0 0 -1.3373 0 0 0 0.5082 矩阵Eigen Vectors的列就是A的特征向量,矩阵Eigen Values的对角线上的元素就是A的特 征值:见81节。 A.5曲线拟合及多项式 多项式可由系数矩阵来表示:见101节。多项式: p(x)=2x3+x2+5x+17 可用向量p=(21517)来表示,而且可用po1yva1命令对任何值进行求值: p=[21517]; polyval(p,0),polyval(p,2) ans 17 ans 47 用命令polyder可对多项式进行微分,并且用命令conv对其进行乘法运算。 pprim polyder(p) pprim 6 2 5 这代表p’(x)=6x2+2xr+5。 psquare conv(p,p) psquare 4217859170289 这代表p(x)2=4xr+4x+21x+78.x+59x2+170x+289。 下面在同一个图中用三个子图画出这三个多项式。命令subp1ot见133节。 x=1 inspace(-2,2,50);
乘法来解。见7 . 2和7 . 7节。 特征值和特征向量可由命令 e i g求得。例如,对上面的矩阵 A求: 矩阵E i g e n Ve c t o r s的列就是A的特征向量,矩阵E i g e n Va l u e s的对角线上的元素就是A的特 征值;见8 . 1节。 A.5 曲线拟合及多项式 多项式可由系数矩阵来表示;见 1 0 . 1节。多项式: 可用向量p=(2 1 5 17)来表示,而且可用p o l y v a l命令对任何值进行求值: 用命令p o l y d e r可对多项式进行微分,并且用命令 c o n v对其进行乘法运算。 这代表p’(x) = 6x 2+ 2x+ 5。 这代表p(x) 2= 4x 6+ 4x 5+ 2 1x 4+ 7 8x 3+ 5 9x 2+ 1 7 0x+ 2 8 9。 下面在同一个图中用三个子图画出这三个多项式。命令 s u b p l o t见1 3 . 3节。 附录A MAT L A B初步 3 5 3 下载
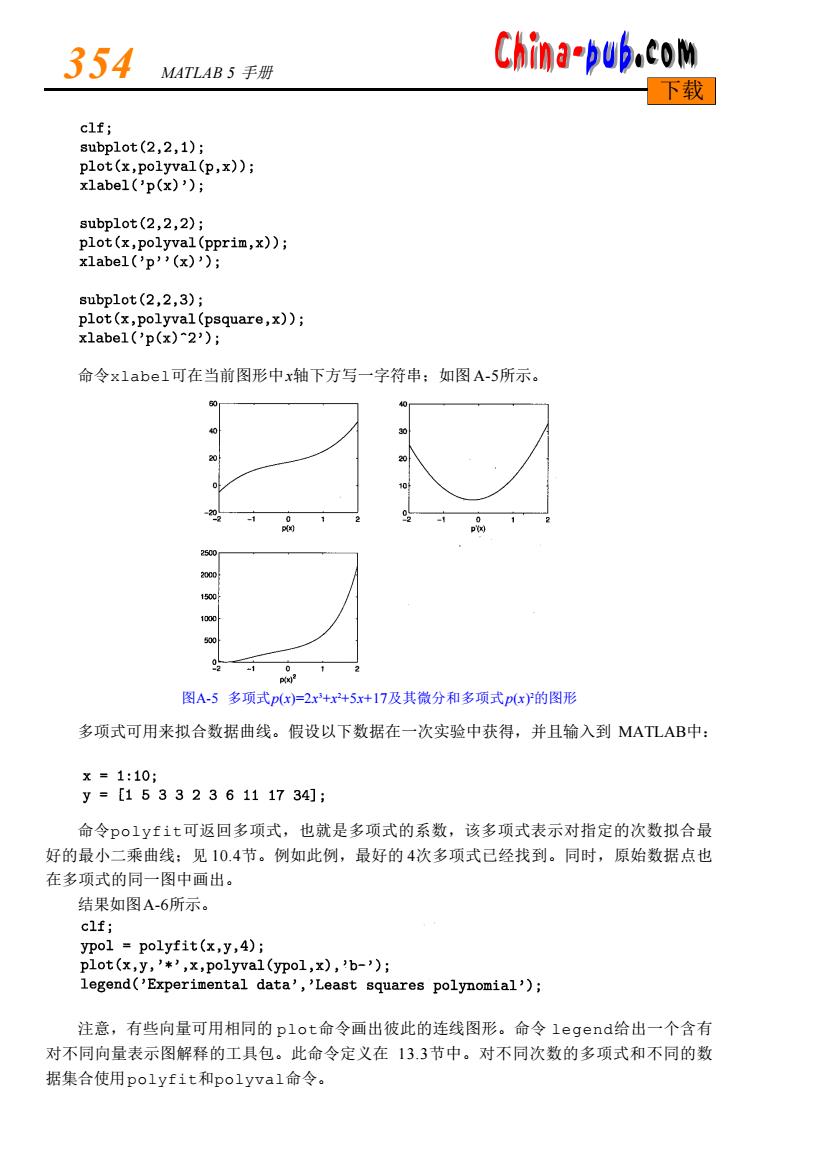
354 MATLAB5手册 China-bub.Com 下载 clf; subp1ot(2,2,1); plot(x,polyval(p,x)); xlabel('p(x)'); 8 ubplot(2,2,2); plot(x,polyval(pprim,x)); xlabel('p'’(x)'); subplot(2,2,3); plot(x,polyval(psquare,x)); x1abe1('p(x)2); 命令x1abe1可在当前图形中x轴下方写一字符串:如图A-5所示。 60 2500 2000 1500 1030 500 2 1 Px) 图A-5多项式p(x)=2x+x+5.x+17及其微分和多项式px)的图形 多项式可用来拟合数据曲线。假设以下数据在一次实验中获得,并且输入到MATLAB中: x=1:10; y=[1533236111734]; 命令polyfit可返回多项式,也就是多项式的系数,该多项式表示对指定的次数拟合最 好的最小二乘曲线:见10.4节。例如此例,最好的4次多项式已经找到。同时,原始数据点也 在多项式的同一图中画出。 结果如图A-6所示。 clf; ypol polyfit(x,y,4); plot(x,y,'*',x,polyval(ypol,x),'b-'); legend('Experimental data','Least squares polynomial'); 注意,有些向量可用相同的plot命令画出彼此的连线图形。命令1 egend:给出一个含有 对不同向量表示图解释的工具包。此命令定义在133节中。对不同次数的多项式和不同的数 据集合使用polyfit和polyva1命令
命令x l a b e l可在当前图形中x轴下方写一字符串;如图A - 5所示。 图A-5 多项式p(x) = 2x 3+x 2+ 5x+ 1 7及其微分和多项式p(x) 2的图形 多项式可用来拟合数据曲线。假设以下数据在一次实验中获得,并且输入到 M AT L A B中: 命令p o l y f i t可返回多项式,也就是多项式的系数,该多项式表示对指定的次数拟合最 好的最小二乘曲线;见 1 0 . 4节。例如此例,最好的 4次多项式已经找到。同时,原始数据点也 在多项式的同一图中画出。 结果如图A - 6所示。 注意,有些向量可用相同的 p l o t命令画出彼此的连线图形。命令 l e g e n d给出一个含有 对不同向量表示图解释的工具包。此命令定义在 1 3 . 3节中。对不同次数的多项式和不同的数 据集合使用p o l y f i t和p o l y v a l命令。 3 5 4 M ATLAB 5 手册 下载
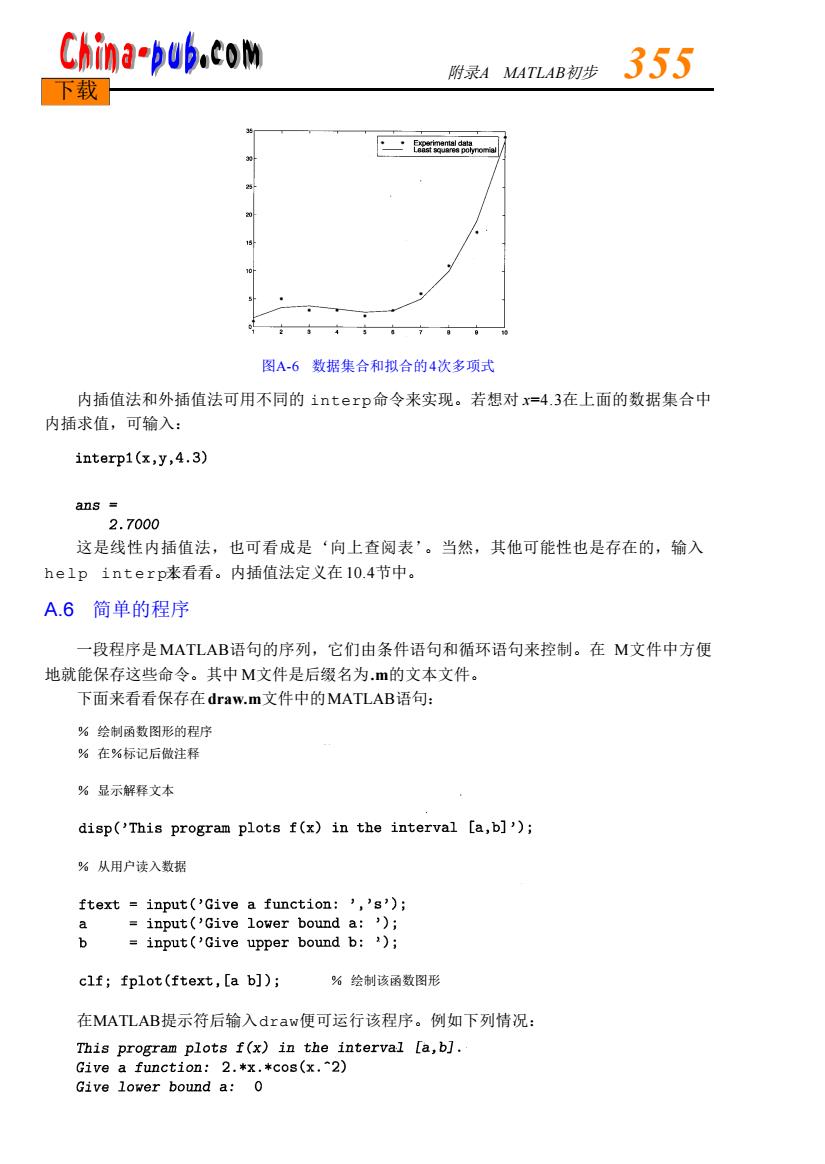
China-pub.com 附录A MATLAB初步 355 下载 图A-6数据集合和拟合的4次多项式 内插值法和外插值法可用不同的interp命令来实现。若想对x=4.3在上面的数据集合中 内插求值,可输入: interp1(x,y,4.3) ans 2.7000 这是线性内插值法,也可看成是‘向上查阅表’。当然,其他可能性也是存在的,输入 he1 p interp来看看。内插值法定义在10.4节中。 A.6简单的程序 一段程序是MATLAB语句的序列,它们由条件语句和循环语句来控制。在M文件中方便 地就能保存这些命令。其中M文件是后缀名为.m的文本文件。 下面来看看保存在draw.m文件中的MATLAB语句: %绘制函数图形的程序 %在%标记后做注释 %显示解释文本 disp('This program plots f(x)in the interval [a,b]'); %从用户读入数据 ftext input('Give a function:','s'); a input('Give lower bound a:') b input('Give upper bound b:') clf;fplot(ftext,[a b]); %绘制该函数图形 在MATLAB提示符后输入draw便可运行该程序。例如下列情况: This program plots f(x)in the interval [a,b]. Give a function:2.*x.*cos(x.2) Give lower bound a:0
图A-6 数据集合和拟合的4次多项式 内插值法和外插值法可用不同的 i n t e r p命令来实现。若想对 x= 4 . 3在上面的数据集合中 内插求值,可输入: 这是线性内插值法,也可看成是‘向上查阅表’。当然,其他可能性也是存在的,输入 help interp1来看看。内插值法定义在1 0 . 4节中。 A.6 简单的程序 一段程序是M AT L A B语句的序列,它们由条件语句和循环语句来控制。在 M文件中方便 地就能保存这些命令。其中 M文件是后缀名为. m的文本文件。 下面来看看保存在d r a w. m文件中的M AT L A B语句: 在M AT L A B提示符后输入d r a w便可运行该程序。例如下列情况: 附录A MAT L A B初步 3 5 5 下载 % 绘制函数图形的程序 % 在%标记后做注释 % 显示解释文本 % 从用户读入数据 % 绘制该函数图形
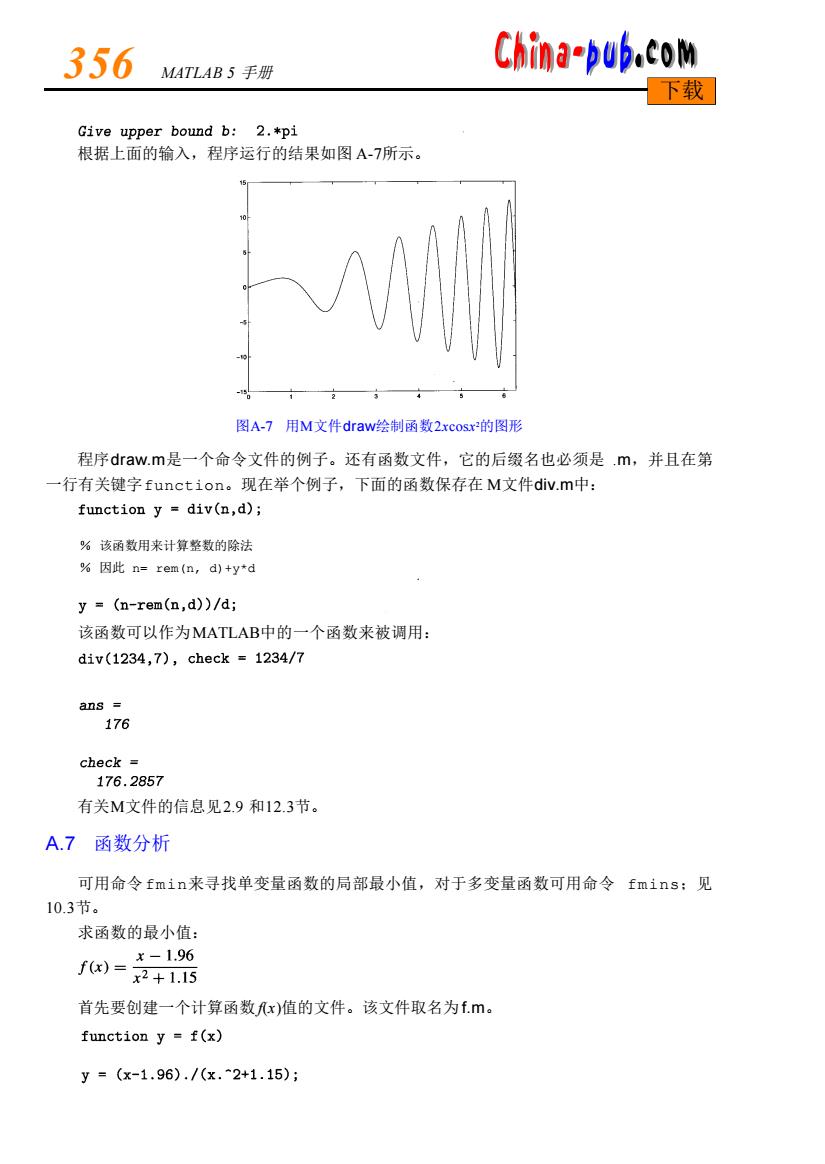
356 MATLAB5手册 China-pub.com 下载 Give upper bound b:2.*pi 根据上面的输入,程序运行的结果如图A-7所示。 图A-7用M文件draw绘制函数2 xCOSx的图形 程序draw.m是一个命令文件的例子。还有函数文件,它的后缀名也必须是.m,并且在第 一行有关键字function。现在举个例子,下面的函数保存在M文件div.m中: function y div(n,d); %该函数用来计算整数的除法 %因此n=rem(n,d)+y*d y =(n-rem(n,d))/d; 该函数可以作为MATLAB中的一个函数来被调用: div(1234,7),check=1234/7 ans 176 check 176.2857 有关M文件的信息见2.9和12.3节。 A.7函数分析 可用命令fmin来寻找单变量函数的局部最小值,对于多变量函数可用命令fmins:见 10.3节。 求函数的最小值: f(x)= x-1.96 x2+1.15 首先要创建一个计算函数fx)值的文件。该文件取名为f.m。 function y f(x) y=(x-1.96)./(x.2+1.15);
根据上面的输入,程序运行的结果如图 A - 7所示。 图A-7 用M文件d r a w绘制函数2xc o sx 2的图形 程序d r a w. m是一个命令文件的例子。还有函数文件,它的后缀名也必须是 .m,并且在第 一行有关键字f u n c t i o n。现在举个例子,下面的函数保存在 M文件d i v. m中: 该函数可以作为M AT L A B中的一个函数来被调用: 有关M文件的信息见2.9 和1 2 . 3节。 A.7 函数分析 可用命令f m i n来寻找单变量函数的局部最小值,对于多变量函数可用命令 f m i n s;见 1 0 . 3节。 求函数的最小值: 首先要创建一个计算函数f(x)值的文件。该文件取名为f . m。 3 5 6 M ATLAB 5 手册 下载 % 该函数用来计算整数的除法 % 因此 n= rem(n, d)+y*d