
试卷代号:1012 座位号■ 中央广播电视大学2007一2008学年度第二学期“开放本科”期末考试(半开卷) 计算机数学基础(2)试题 2008年7月 题 号 二 三 四 总 分 分 数 得 分 评卷人 一、单项选择题(每小题4分,共20分) 得分☐1. π=3.141592653…的五位有效数字,它的绝对误差限是π的左起第五位的半个单 位,即绝对误差限是( A.0.0005 B.0.00005 C.0.000005 D.0.0000005 1x1+2x2+x3=0 得分 2.用列主元消去法解线性方程组{2x1十2x2十3x3=3作第一次消元后得到的第三 -x1-3x2=2 个方程是( A.-x2+x3=2 B.一2x2十x3=3 C.x2-0.5x3=-1.5 D.-2x2+1.5x3=3.5 x1十2x2-2xg=1 得分 3.用高斯一赛德尔迭代法解线性方程组}x1十x2一x3=3的迭代公式中 2x1+2x2+x3=5 x+=( )(k=0,1,2,…). A.3-x十x B.3-x+x+ C.3-++ D.3-x+》+x+D 84
试卷代号 :1012 座位号口口 中央广播电视大学2007-2008学年度第二学期“开放本科”期末考试(半开卷) 计算机数学基础(2) 试题 2008年 7月 题 号 四 总 分 分 数 得 分 评卷人 一、单项选择题 (每小题 4分 ,共 20分) 匣三口1.二一3.141592653…的五位有效数字,它的绝对误差限是二的左起第五位的半个单 位 ,即绝对误差限是( ). 0.0005 0.000005 B. 0.00005 D. 0.0000005 A C. _ (x1 +2x2 +x3一。 瞪且 」2·用列主元消去法解线性方程组} t 2一xx,十】一2x 3 2x十 2=3x 2 3 =3作第一次消元后得到的第三 个方程是( )。 A.一x2 +x3“2 B.一2x2 +x3 =3 C. x2一0. 5x3“一l. 5 D.一2x:十1. 5X3=3. 5 、3. ···-······……{ x1 +2x2一2x3“ 1 x1-+2-x3=3 的迭代公式中 2x,+2x:十x3=5 x妾k+1)=( )(k=0,1,2,…). A. 3一斌k) +x3ck) C. 3一x护+‘’+x梦, B. 3一x(1 k) +x(3k+1) D. 3一x护千‘’+二;k+1)

得分 4.已知当x=1,2时的函数值为f(1),f(2)时,则f(1)≈(). A.f(1)-f(2) B.f(2)-f(1) C2f)+f2)] D.2f2)-f1] (y'=xy(0≤x≤0.6) 得分州 5.取h=0.2,用欧拉法求初值问题 在x=0.2,0.4,0.6处的数 (y(0)=1 值解的公式y4+1=( ),k=0,1,2. A.(1+0.2x)y% B.yo十0.2xye C.y十xye D.(0.2十xe)ye 得分 评卷人 二、填空题(每小题4分,共20分】 得分 6.要使√20=4.472135…的近似值的相对误差限小于0.1%,则近似值至少要取 位有效数字. 得分 7. 设近似值x1,x2的绝对误差限分别为e(x1),e(x2),则e(x1x2)= 1 0.750.757 得分 8.设线性方程组AX=b的系数矩阵为A=0.751 0.75那么雅可比迭代矩 0.750.751 阵B。= 得分 9.已知数据(1,3.8),(2,7.2),(3,10),用拟合曲线拟合这些点,计算得法方程组 为 得分州 10.用牛顿法求方程f(x)=0在[a,b]内的根,已知f(x)在[a,b]内不为0,f"(x)在[a,b] 内不变号,那么选择初始值x。满足 ,则它的迭代解数列一定收敛到方程f(x)=0的根. 85
瘾州 卜已知当x=1,2 f(1)一f(2) 时的函数值为f(1),f(2)时,则厂(1)} B. f(2)一f(i) 合〔, “ ,-}- f<2)] D.喜 乙 [f (2)一f(1)] A. C. 藏不门。.取*一。.2,用欧拉法求初值问题丁了_一‘ y(0-<x. 6’在二一。.。,。.、,。.。处的数 — ly(o)=1 值解的公式 yk+i = A.(1+0. 2x,) yk C. y*十xkyk ),k=0,1,2. B. y。十0. 2xkyk D. (0. 2十xk) yk 得 分 评卷人 二 、填空题 (每小题 4分 .共 20分) {画口 6.要使俪一‘.472135…的近似值的相对误差限小于0. 1 0 o,则近似值至少要取 位有效数字. 匣王口7·设近似值x1 ,x2的绝对误差限分别为。(xl),e(x2),则。(x, x,)= _ 干‘ h '3} 18.“线”方程”AX=“的系”矩阵“A一 四 0.. 0.75 75 1 0. 75 0. 75}那么雅可比迭代矩 75 0.75 1 阵Bo= 匣亚口9.已知数据(1, 3.8),(2, 7.2),(3, 10),用拟合曲线拟合这些点,计算得法方程组 匣王口10.用牛顿法求方程f(x)一。A[a,b]内的根,已知/f (x)-A[a,b]内不为。,f"(x)在〔。,习 内不变号 ,那么选择初始值 xo满足 ,则它的迭代解数列一定收敛到方程_f (x) =0的根

得分 评卷人 三、计算题(每小题15分,共30分) 得分 11.已知函数值f(0)=6,f(1)=10,f(3)=46,f(4)=82,f(6)=212,求函数的四阶 均差f(0,1,3,4,6)和二阶均差f(4,1,3). 得分 12.设求积公式∫,fx)dz≈A,f(-a)+Af0)十Af@)试求待定系数A,A A2使得该求积公式的代数精度尽量高. 得分 评卷人 四、计算分析题(每小题15分,共30分】 得分州 13.用弦截法求方程x一sinx一0.5=0在[1.4,1.6]之间的一个近似根,满足 |x+1一x≤0.01.保留4位小数. y'=x-y+1 得分 14.用四阶龙格一库塔法求解初值问题 已经计算得x=0.4时, y(0)=1 y(0.4)≈1.0704,求x=0.8处的数值解.保留4位小数.已知四阶龙格一库塔法 公式为=-f+,+合),-f0+号,%十受), =f云+h,%+h),*1=%+合(+2+2a十) 86
得 分 评卷人 三、计算题(每小题 15分,共 30分) 匣亚] 11.已知函数值f(0)=6, f(1)=10, f(3)=46, f(4)=82,f(6) =212,求函数的四阶 均差 f(0, 1, 3, 4, 6)和二阶均差 f(4, 1, 3). 匣亚]12·设求积公式分(二,dx-^.-A,f(一,+A, f(0) +A2 f(a,试求待定系数Ao,A, A:使得该求积公式的代数精度尽量高. 得 分 评卷人 四、计算分析题(每小题 15分,共 30分) f'}州 }13.用弦截法求方程 x - si。 一。.5=0在〔1.4,1.6〕之间的一个近似根,满足 I-k+1 -xk I <0. 01.保留4位小数. 0州 卜. 夕二x一y十1 已经计 算得 x=0. 4时, y(0. 4)-1. 0704,求 x=o. 8 ty(o)一 1 处的数值解.保留 4位小数. 用四阶龙”一库塔法求””“问题{ 已知四阶龙格一库塔法 公式为 K, 1, 。h = f (xk,yk),K2= flx*十 -; 白;-h,y*十 .万自 Ki), K3 1, .h = flx;十 o 乙 h,yk卞 W 乙 K2), ‘;=f(xk+h,yk+hic3), yk+1 h , .‘ =y*十 飞 v犷kKl十 LiceT-2K,+ic,)
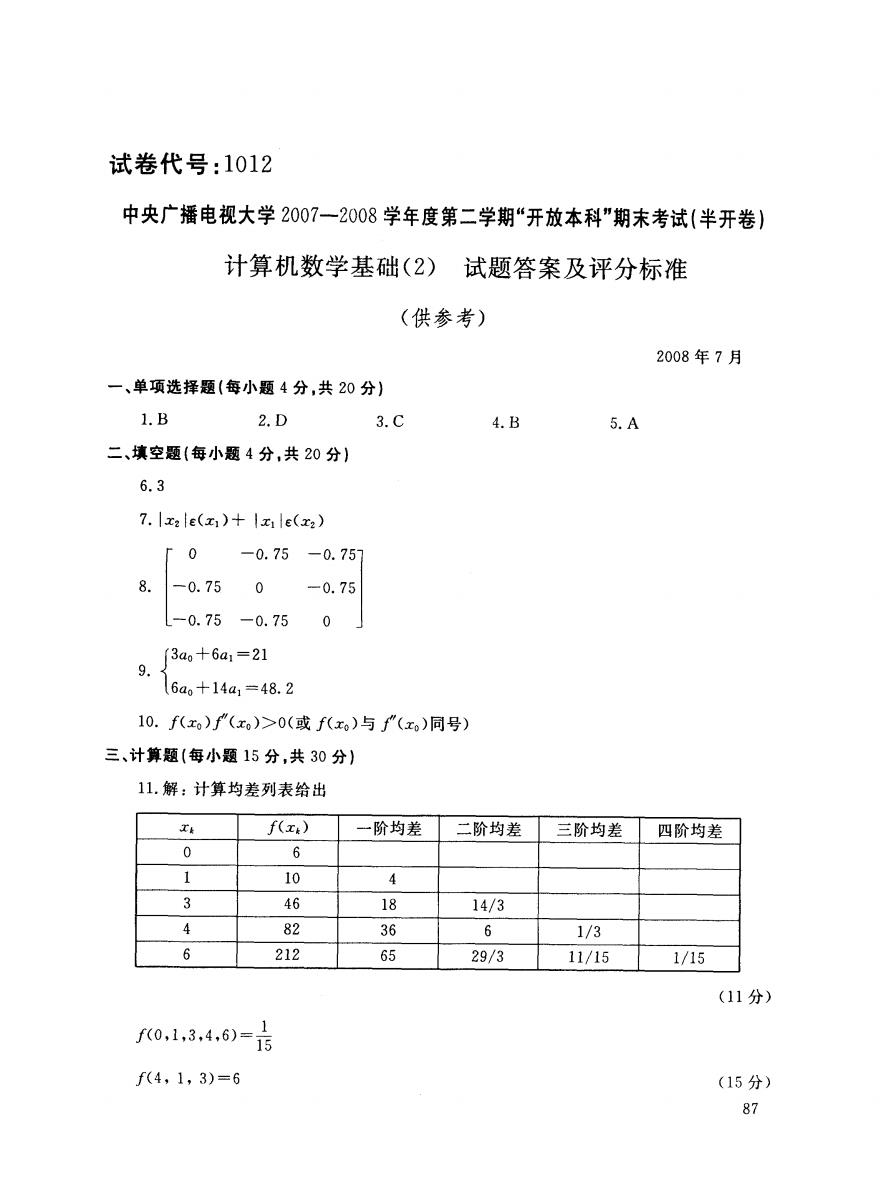
试卷代号:1012 中央广播电视大学2007一2008学年度第二学期“开放本科”期末考试(半开卷) 计算机数学基础(2)试题答案及评分标准 (供参考) 2008年7月 一、单项选择题(每小题4分,共20分)】 1.B 2.D 3.C 4.B 5.A 二、填空题(每小题4分,共20分)】 6.3 7.|x2e(x1)+|x1e(x2) ro -0.75-0.75 8. -0.75 0 -0.75 L-0.75-0.75 0 f3a0+6a1=21 9. (6a+14a1=48.2 10.f(x)f"(xo)>0(或f(x。)与"(x)同号) 三、计算题(每小题15分,共30分) 11.解:计算均差列表给出 x f(x:) 一阶均差 二阶均差 三阶均差 四阶均差 0 6 1 10 4 3 46 18 14/3 4 82 36 6 1/3 6 212 65 29/3 11/15 1/15 (11分) f0,134,60= f(4,1,3)=6 (15分) 87
试卷代号:1012 中央广播电视大学2007-2008学年度第二学期“开放本科”期末考试(半开卷) 计算机数学基础(2) 试题答案及评分标准 (供参考) 2008年 7月 一、单项选择题(每小题 4分.共 20分) 1. B 2. D 3. C 4.B 5. A 二、填空题(每小题 4分.共 20分} 6.3 7. I X2}e(x,)+ !x,}e(x2) 一 0. 75 一 0. 75 .75 0 .75 一 0.75 一 0.75一 0 0 0 一 一 r l 一 L O U 3ao+6a, =21 6a。十14a, =48. 2 ‘ 1 , 、 ra t O J 10. f(xo)f"(xo)>0(或f(xo)与f}(xo)同号) 三、计算题(每小题 15分,共 30分) 11.解:计算均差列表给出 x& f(xk) 一 阶均差 二阶均差 三阶均差 四阶均差 0 6 1 10 4 3 46 18 14/3 4 82 36 6 1/3 6 212 65 29/3 11/15 1/15 (11分) 1 J火U,工,S,任,。)=15 _f( 4,1,3)=6 (15分) 87

12.解:因为有三个待定参数,至少列出三个方程,令f(x)=1,x,x2,代入求积公式,得到 2a=A+A1+A2 0=-Aoa+Aza (6分) 2u-Aoa2+Aza* 解得A。=A=号,A=号 (9分) 求积公式为∫,f(x)d≈号[f(-a)+4f(0)+f(a)] (13分) 当f(x)=x,使得求积公式精确成立,故该求积公式具有3次代数精度. (15分) 四、计算分析题(每小题15分,共30分)】 13.解:设f(x)=x-sinx-0.5,取x=1.4,x1=1.6,由f(1.4)=一0.08550,故f(x)=0在[1.4,1.6]内有根. (3分) f(x.) 弦截法的公式为zt1=工.fz=xx.一x),《n=1,2,…)(6分) 于是,代人函数f(x),本题有达代公式x+1=x.一x,-1-sinx,十sinu -sinxn-0.5 -(x.一x-1) 1.6-sinl.6-0.5 =1.6-1.6-14-sin6+sinl.41.6-1.4)=1.4919 1x2一x1{=0.1081,不满足精度要求. (10分) 当n=2时, 1.4919-sin1.4919-0.5 x=1.49191.4919-.6=9m.4919十sinl.61.4919-1.6)=1.4970 |x3一x2|=0.0051,满足精度要求. 所求方程的解为x·≈1.4970 (15分) 14.解:h=0.4,x0=0,y%=1, 1=x&ya十1 k2=x4十0.2-y4-0.2k1+1 k3=xk十0.2一ye-0.2e2+1 88
12.解:因为有三个待定参数,至少列出三个方程,令 f(x)=1,x,x2,代人求积公式,得到 2a=A,+A,十AZ 0=一Aoa+A2a (6分) 2a3 一二:- = H na - rt A 2a" 3 4a 解得 Ao =A2=尽 d ,A,= 一3’ (9分) 求积公式为扮(二)dx ti答J If(一a)+4f(0)+f(a) ] (13分) 当f(x)二x3,使得求积公式精确成立,故该求积公式具有3次代数精度. (15分) 四、计算分析题 (每小题 15分,共 30分》 13.解:设 f(x) =x一si二 一0.5,取xo=1.4,x1“1.6,由 f(1.4)二一。。08550,故f(x)=0在〔1.4, 1.6〕内有根. (3分) 弦截法的公式为:x.+1 =x。一 了(x) ,___ _ 、 , _, 。 兀币二万不xn-巧1)}-tn工。一‘少八”一土’‘ …)(6分) 于是 ,代人 函数 了(x),本题有迭代公式 x+1 =x.一 x二一sinx。一0.5 x,一x,一1一sinx,十 sinx。一1 (x,一x,一I) 1.6一 sinl. 6一0.5 = l. b一 二-言一-二一气尸---,-下一气丁气~~二-丁~.ll 1. b 一 1.4 一 sln l. b ,一sln l. 4 6一 1.4)= 1.4919 }x2一 x1}=。.1081,不满足精度要求. 当 n=2时, (10分) 4919一 1.4919一 sinl. 4919一 0. 5 丁--气气丁:,:--.弋,-二--- 二~代尸一叮气:二叫弋尸气一-丁-竺丁--二 11 1.4919一 1. 一 sinl. 491,十 sin!. ti 4919一 1. 6)“1.4970 I x,一x2!=0. 0051,满足精度要求. 所求方程的解为 x' -1. 4970 14.解 :h=0.4,x,=0,y,=1, K1 =x*一yk+1 ice = xk +o. 2一y*一0. 2K, +1 K, =.-k +0. 2一y*一0. 2K2+1 (15分)

k4=xk十0.4-ye-0.4K3+1 (5分) 已知x1=0.4,y1=1.0704时,求当x2=0.8时,y2的值. %1=x1-y1十1=0.4-1.0704+1=0.3296 =x1+0.2-y1-0.21+1=0.4637 k3=x1+0.2-y-0.2e2+1=0.4369 k4=x1十0.4-y1-0.4k3十1=0.5548 (12分) 为=y+合+2+2%+e) =1.0704+0(0.3296+2X0.4637+2X0.4369+0.548)=1.2494 (15分) 89
as=xk+0. 4一y;一0. 4/C3+1 已知x, =0. 4,y, =1. 0704时,求当x2 =0. 8时,y:的值 a, = x,一yi+1=0. 4一1. 0704+1=0. 3296 Ice =x, +0. 2一yi一0. 21c,+1=0. 4637 a3 =xl +0. 2一y,一0. 2K2+1=0. 4369 Ka =xi +0. 4一yi一0. 4K,+1=0. 5548 h , y2 =yI+于 (IC, +2K, +2K,+。) 护‘ J二’6、“且’一“乙’“几3’几4产 (5分) (12分) _,_,,0.4,_ ____ _. _ ___ ._ 一1.。/U4一6 kU. Jz9b一Z x 0. 463'/+Z X 0. 4369+0.5548)=1.2494 (15分) 89