内蒙古科技大学：《材料力学》课程PPT教学课件（机械类）第七章 应力状态分析 强度理论

第七章应力状态分析强度理论

1 第七章 应力状态分析 强度理论

第七章强度理论应力状态分析应力状态的概念口口二向应力状态分析一一解析法口二向应力状态分析—一图解法三向应力状态口广义胡克定律国复杂应力状态下的应变能密度口强度理论概述口四种常见的强度理论及强度条件

2 第七章 应力状态分析 强度理论  应力状态的概念  二向应力状态分析——解析法  二向应力状态分析——图解法  三向应力状态  广义胡克定律  复杂应力状态下的应变能密度  强度理论概述  四种常见的强度理论及强度条件 目 录

s 71应力状态的概念铸铁低碳钢塑性材料拉伸时为什么会出现滑移线？一

3 低碳钢 塑性材料拉伸时为什么会出现滑移线？ 铸 铁 §7—1 应力状态的概念

$71应力状态的概念铸铁低碳钢脆性材料扭转时为什么沿45°螺旋面断开？

4 脆性材料扭转时为什么沿45º螺旋面断开？ 低碳钢 铸 铁 §7—1 应力状态的概念

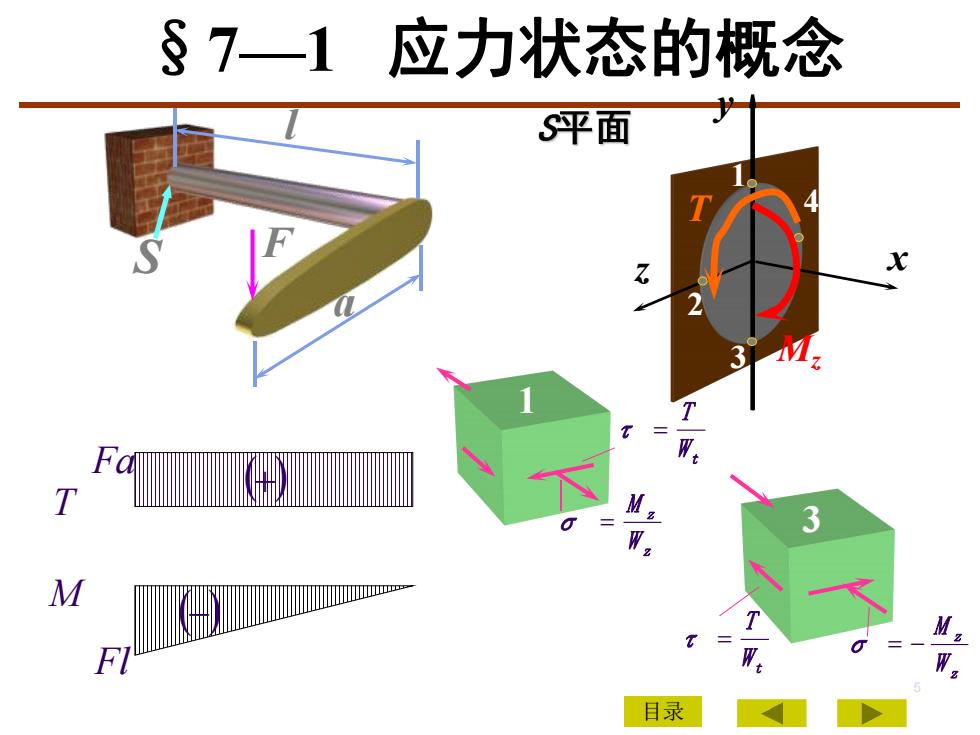
s 71应力状态的概念S平面xNHOTMM,2FlRW目录

5 F l a S 1 W t T τ  z z W M σ  3 W t T τ  z z W M σ   z Mz T 4 3 2 1 y x M  Fl T  Fa 目录 §7—1 应力状态的概念

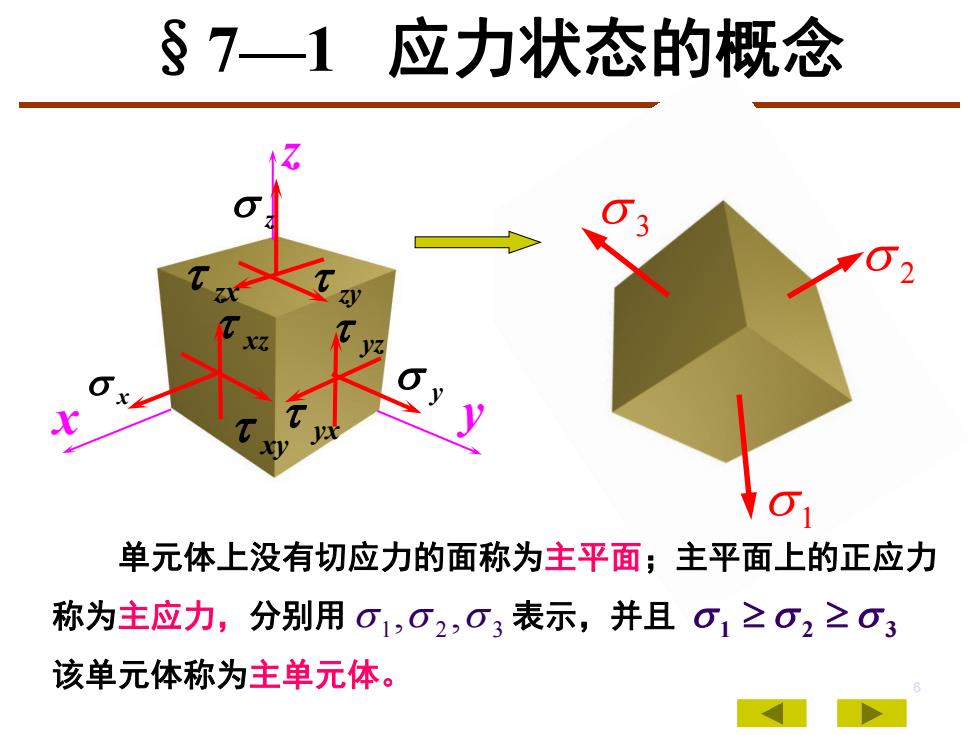
$71应力状态的概念20102TTZLZXZZaJL10单元体上没有切应力的面称为主平面；主平面上的正应力称为主应力，分别用1,02,03表示，并且01≥02≥03该单元体称为主单元体

6  1  2  3 x y z  x  y  z  xy  yx  yz  zy  zx  xz 单元体上没有切应力的面称为主平面；主平面上的正应力 称为主应力，分别用 表示，并且 该单元体称为主单元体。 1 2 3  , ,  1   2   3 §7—1 应力状态的概念

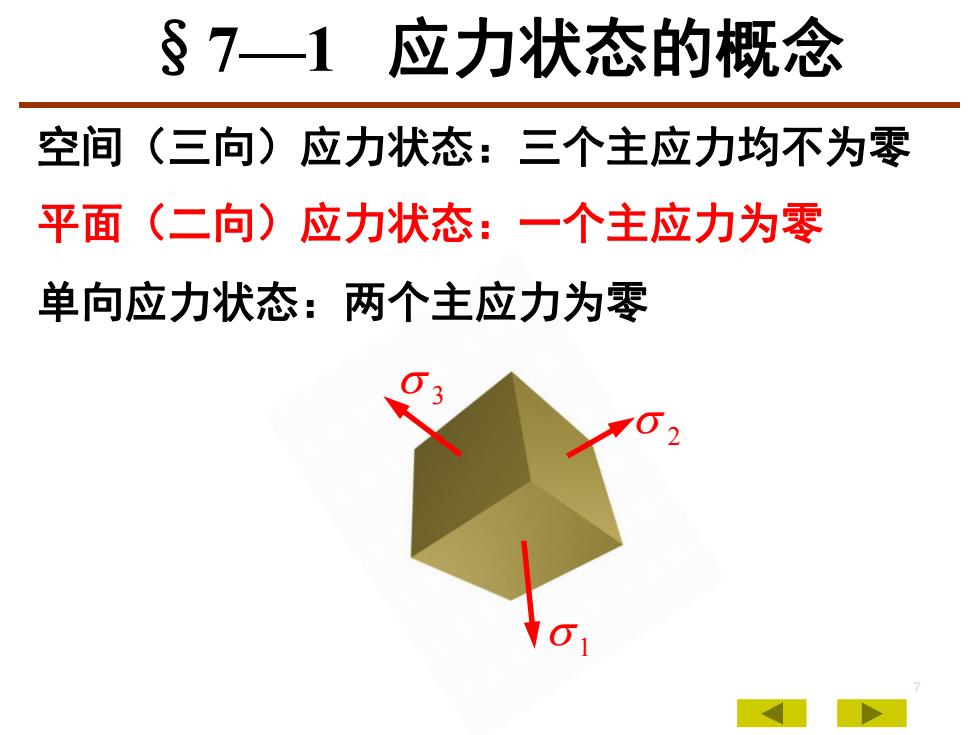
s71应力状态的概念空间 (三向)应力状态：三个主应力均不为零平面（二向)应力状态：一个主应力为零单向应力状态：两个主应力为零DO101

7  1  2  3 空间（三向）应力状态：三个主应力均不为零 平面（二向）应力状态：一个主应力为零 单向应力状态：两个主应力为零 §7—1 应力状态的概念

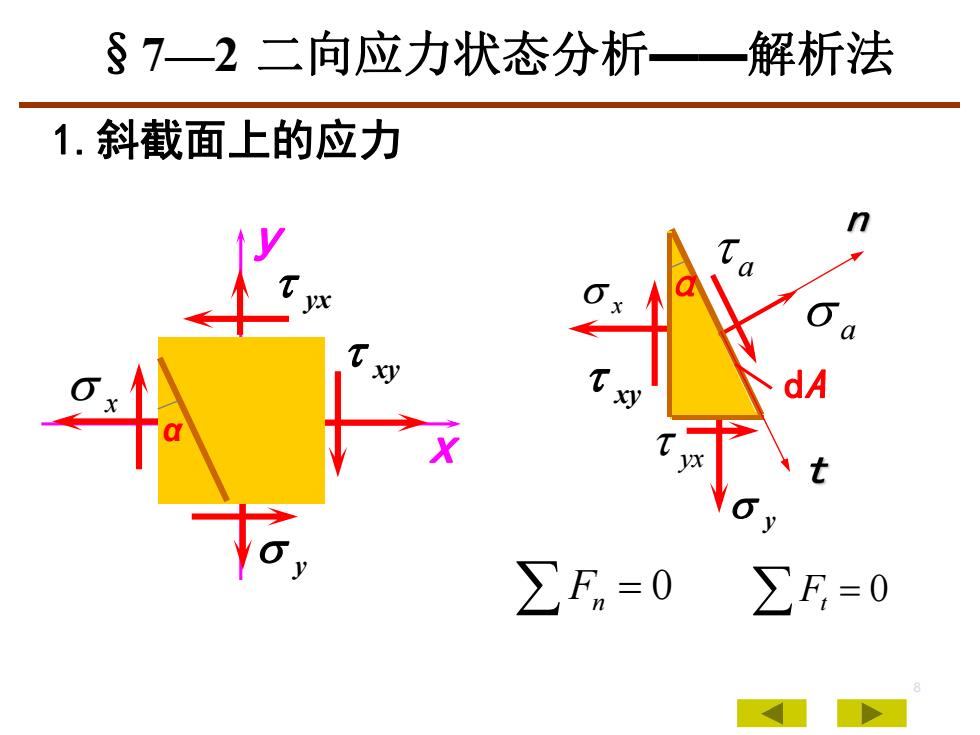
s 7—2 二向应力状态分析——解析法1.斜截面上的应力nT.q20yx0dTxyTxdAO2Xyxt0yZF,=0F,=0E

8 x y  x  y  yx  xy α   0 Fn   0 Ft 1.斜截面上的应力  y  a a   xy dA  x α yx  §7—2 二向应力状态分析——解析法

s7—2 二向应力状态分析—一解析法nKo列平衡方程OaX9aZF,=0TxydAT.&dA+tx(dAcosα)sinα-o,(dAcosα)cosα +yxtOT(dAsinα)cosα-,(dAsinα)sinα = 0ZF=0tadA-tx,(dAcosα)cosα-o,(dAcosα)sinα+Tyx(dAsinα)sinα+o,(dAsinα)cosα = 0

9 Fn  0 ( sin ) cos ( sin )sin 0 ( cos )sin ( cos ) cos                    dA dA dA dA dA yx y xy x Ft  0 ( sin )sin ( sin ) cos 0 ( cos ) cos ( cos )sin                    dA dA dA dA dA yx y xy x  y  a a   xy dA  x α yx  §7—2 二向应力状态分析——解析法

s7—2 二向应力状态分析——解析法cos α ==(1+ cos 2α)2利用三角函数公式sin’ α ==(1-cos 2α)22sinα cosα = sin 2α并注意到 x=x,化简得Gα=(0, +0,)+(o,-0,)cos 2α-T y sin 2α=(αx-0,)sin 2α+tx cos2α

10 利用三角函数公式 (1 cos 2 ) 2 1 cos 2    (1 cos 2 ) 2 1 sin 2    2sin cos  sin2 { 并注意到  yx   xy 化简得     (  ) cos 2  sin 2 2 1 ( ) 2 1  x  y  x  y  xy   (  )sin 2  cos 2 2 1  x  y  xy §7—2 二向应力状态分析——解析法