内蒙古科技大学：《材料力学》课程PPT教学课件（机械类）附录——平面图形的几何性质

附录I平面图形的几何性质sI-1 静矩和形心1.静矩ZS, =J, ydAdAZ S,=[, zdA0L→

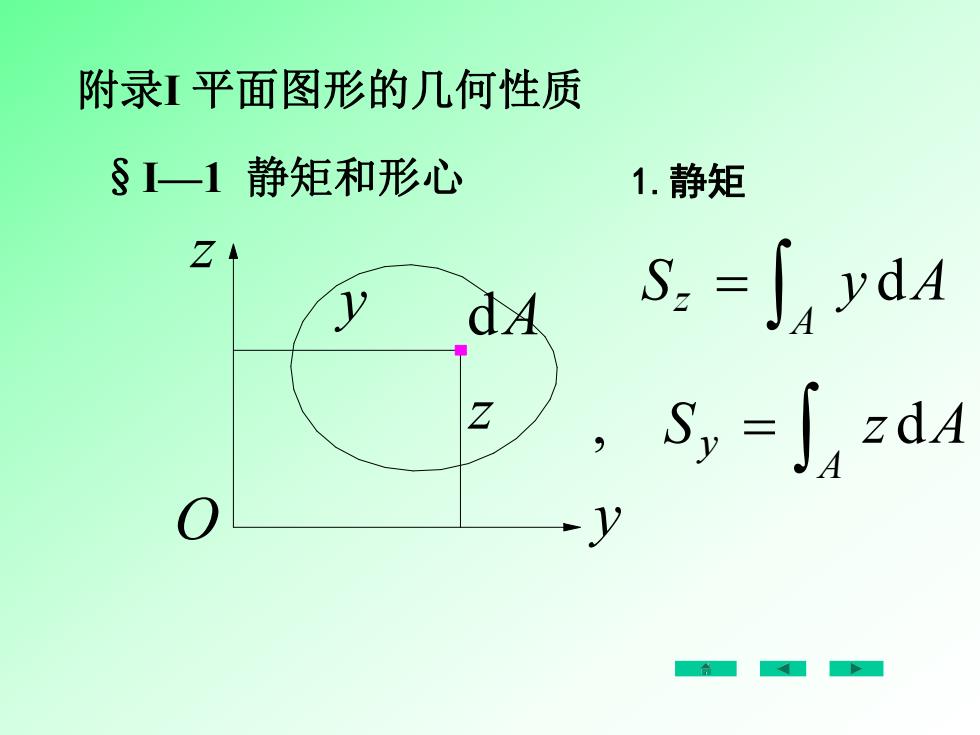
§I—1 静矩和形心 dA y y z z O Sz y A A   d , Sy z A A   d 附录I 平面图形的几何性质 1.静矩

AZ形心坐标：y.CzOydAzdAJAZV1AA

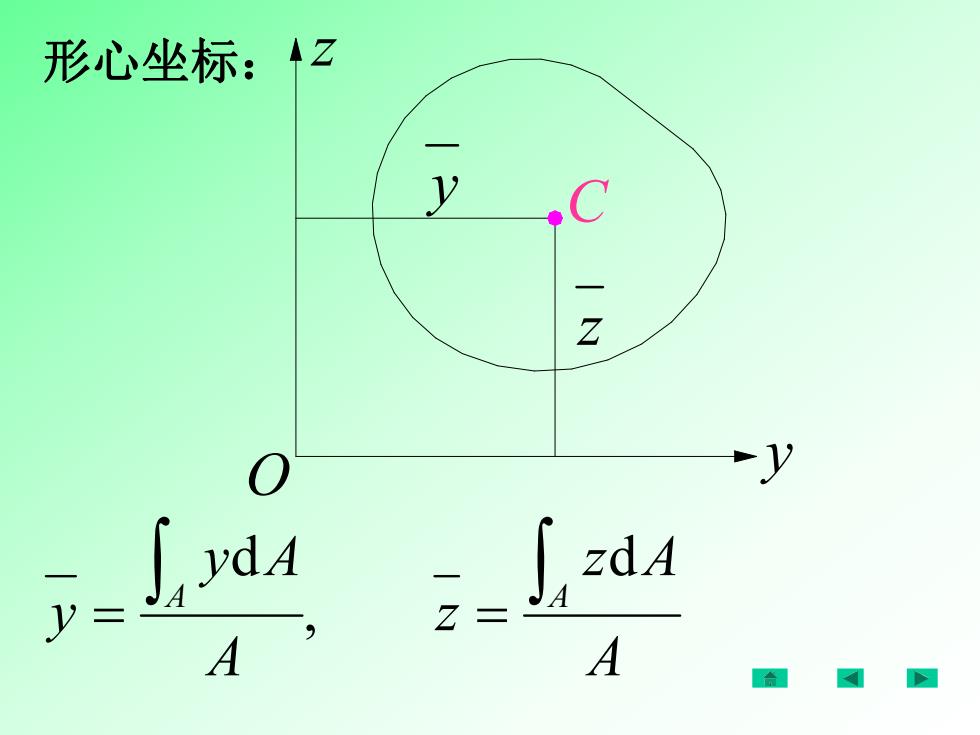
形心坐标： A z A z A y A y A A   d , d C y y z z O

静矩和形心坐标之间的关系：4ZSN二-As-CZAzS, =yA,S,=zA

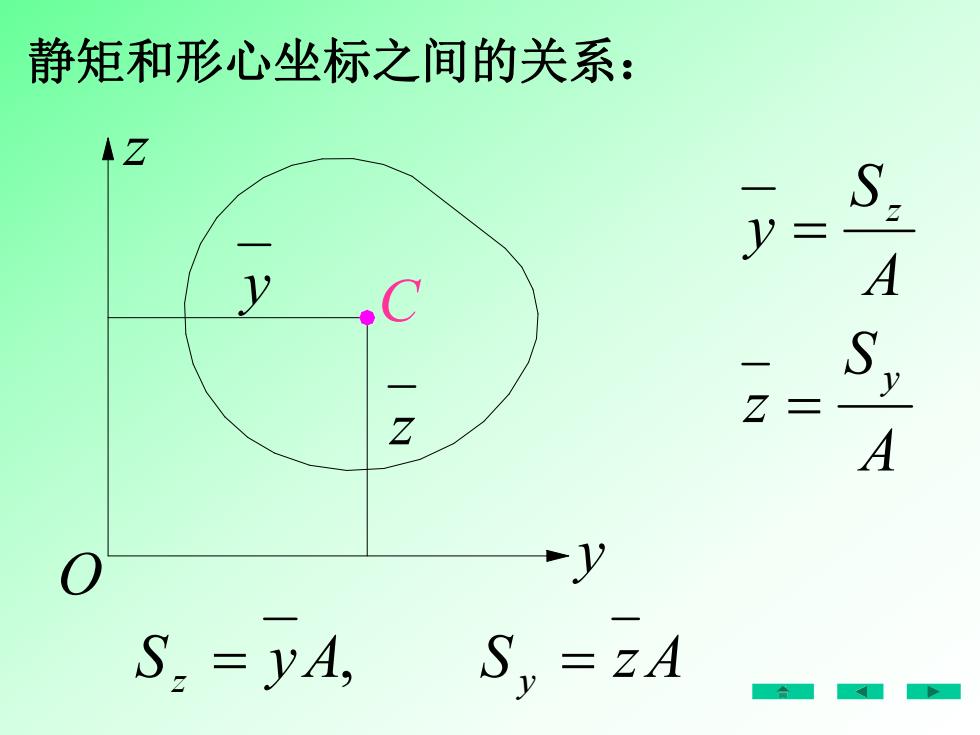
静矩和形心坐标之间的关系： A S z A S y y z   C y y z z O Sz  yA, S y  zA

例：计算由抛物线、y轴和z轴所围成的平面图形对y轴和z轴的静矩，并确定图形的形心坐标Zz = h162y

例：计算由抛物线、y轴和z轴所围成的平面图 形对y轴和z轴的静矩，并确定图形的形心坐标。 z h y b        1  2 2 y z O

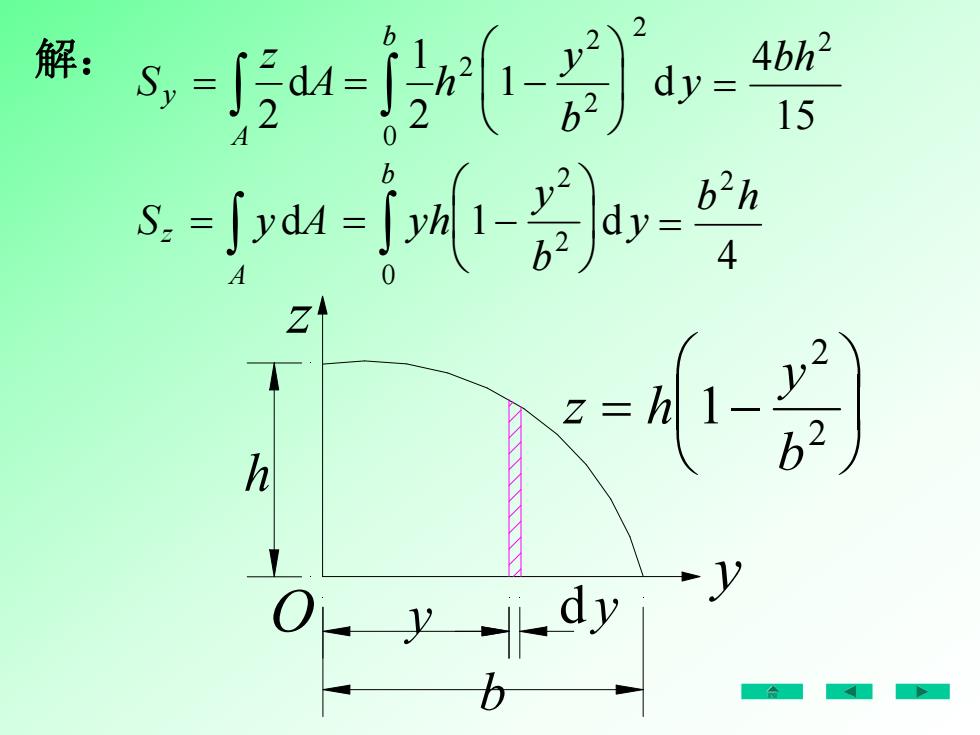
4bh?解： s,=,d-[r(1-号)dy二15b?hS, =[ ydA =J yh( 1--dy624福AZ2L26hVa

z h y b        1  2 2 y d y b h S z y A A   2 解： d Sz y A A   d          1 2 1 0 2 2 2 2 b h y b d y          yh y b y b 0 2 2 1 d y z O  4 15 2 bh  b h 2 4

2bhA=[d4=jn(1-dyA3bh?形心坐标为：S3b4V三2bh8A34bh?S2h15yZ一2bh5A3

A A A   d 形心坐标为: 8 3 3 2 4 2 b bh bh A S y z    5 2 3 2 15 4 2 h bh bh A S z y             0 2 2 1 b h y b d y  2 3 bh

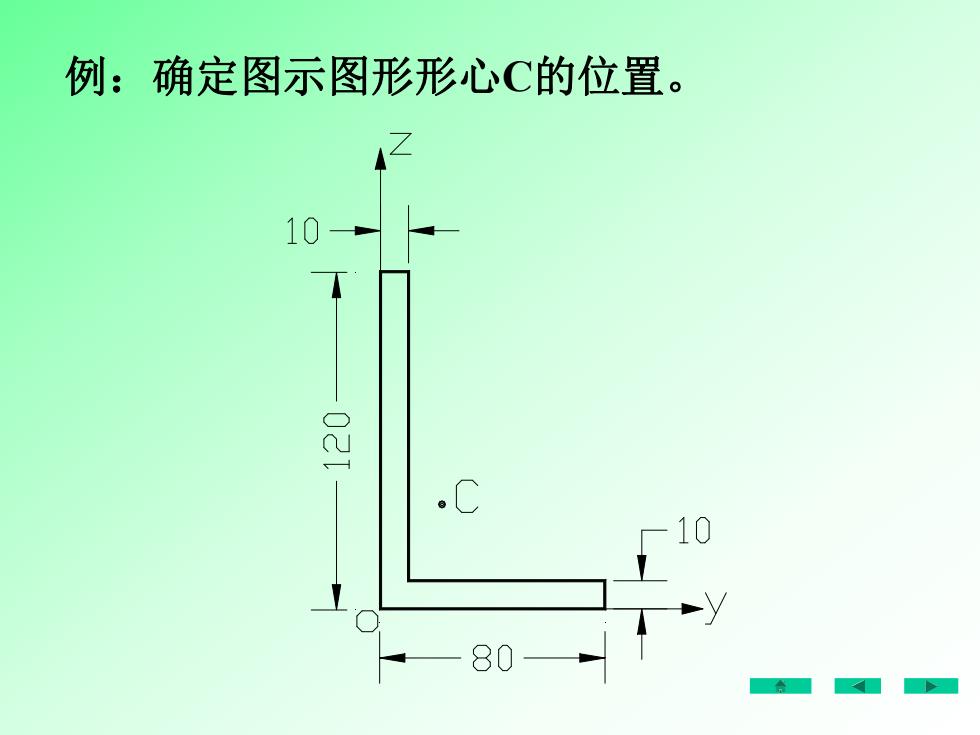
例：确定图示图形形心C的位置。100280

例：确定图示图形形心C的位置

S10×120×5+70×10×45解：7= 19.7mm12A1200+700S10×120×60+70×10×51= 39.7mmA1200+ 70010a.C1080

解： A S y z  39.7mm 1200 700 10 120 60 70 10 5          A S z y         10 120 5 70 10 45 1200 700 19.7mm

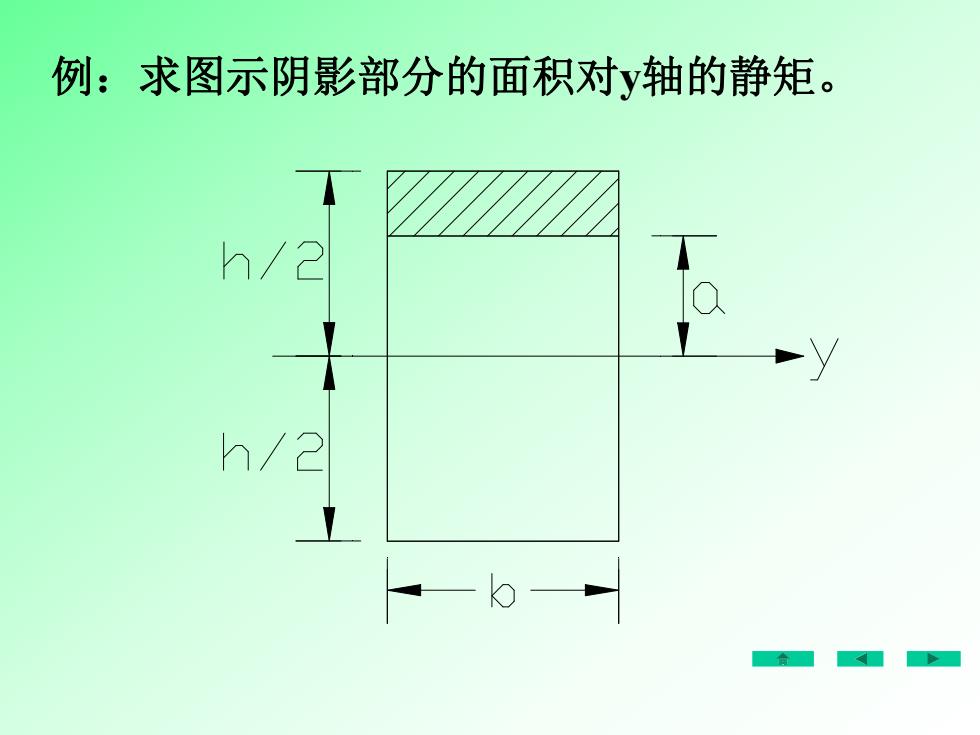
例：求图示阴影部分的面积对y轴的静矩。h/2

例：求图示阴影部分的面积对y轴的静矩

解：三b

S b h a a h a y         2 4 2 解：     b h a 2 42 2