内蒙古科技大学：《材料力学》课程PPT教学课件（土木类）第七章 应力状态和强度理论

第7章应力状态和强度理论S 7-1 概 述1、一点处的应力状态构件内一点处各截面方向上的应力的情况，称为该点的应力状态。可由围绕该点的一个单元体面上的应力表示。目的：通过应力状态分析求出该点处的。max、Tmax及其作用面，从而更好地进行强度分析

第7章 应力状态和强度理论 构件内一点处各截面方向上的应力的情况，称为 该点的应力状态。可由围绕该点的一个单元体面上的 应力表示。 §7-1 概 述 1、一点处的应力状态 目的：通过应力状态分析求出该点处的 max、 max及 其作用面，从而更好地进行强度分析

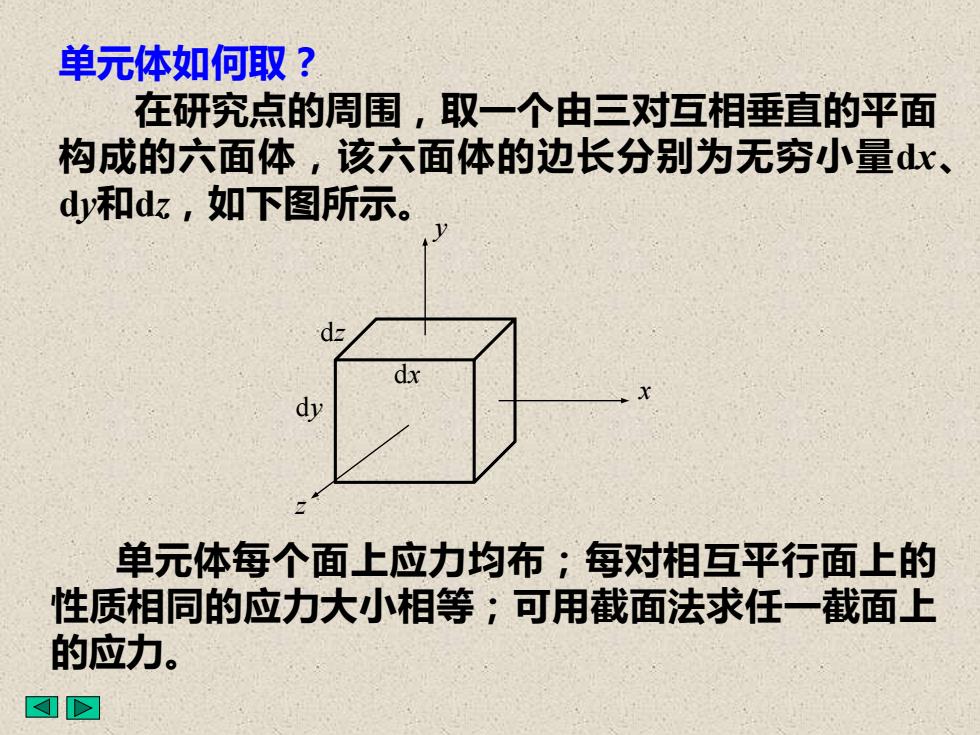
单元体如何取？在研究点的周围，取一个由三对互相垂直的平面构成的六面体，该六面体的边长分别为无穷小量dy和dz，如下图所示。1dy单元体每个面上应力均布：每对相互平行面上的性质相同的应力大小相等；可用截面法求任一截面上的应力

单元体每个面上应力均布；每对相互平行面上的 性质相同的应力大小相等；可用截面法求任一截面上 的应力。 单元体如何取？ 在研究点的周围，取一个由三对互相垂直的平面 构成的六面体，该六面体的边长分别为无穷小量dx、 dy和dz，如下图所示。 dy dz dx z x y

2、强度理论对单轴或纯剪切应力状态，可由实验测得的相应的材料许用应力来建立正应力和切应力强度条件。而当一点处的应力状态较为复杂时，因应力的组合形式有无限多的可能性，不可能由实验的方法来确定每一应力组合下材料的极限应力，因此需确定引起材料破坏的共同因素。关于材料破坏的共同因素（即破坏规律）的假说即称为强度理论。可根据强度理论来建立强度条件

对单轴或纯剪切应力状态，可由实验测得的相应 的材料许用应力来建立正应力和切应力强度条件。 2、强度理论 而当一点处的应力状态较为复杂时，因应力的组 合形式有无限多的可能性，不可能由实验的方法来确 定每一应力组合下材料的极限应力，因此需确定引起 材料破坏的共同因素。 关于材料破坏的共同因素（即破坏规律）的假说， 即称为强度理论。可根据强度理论来建立强度条件

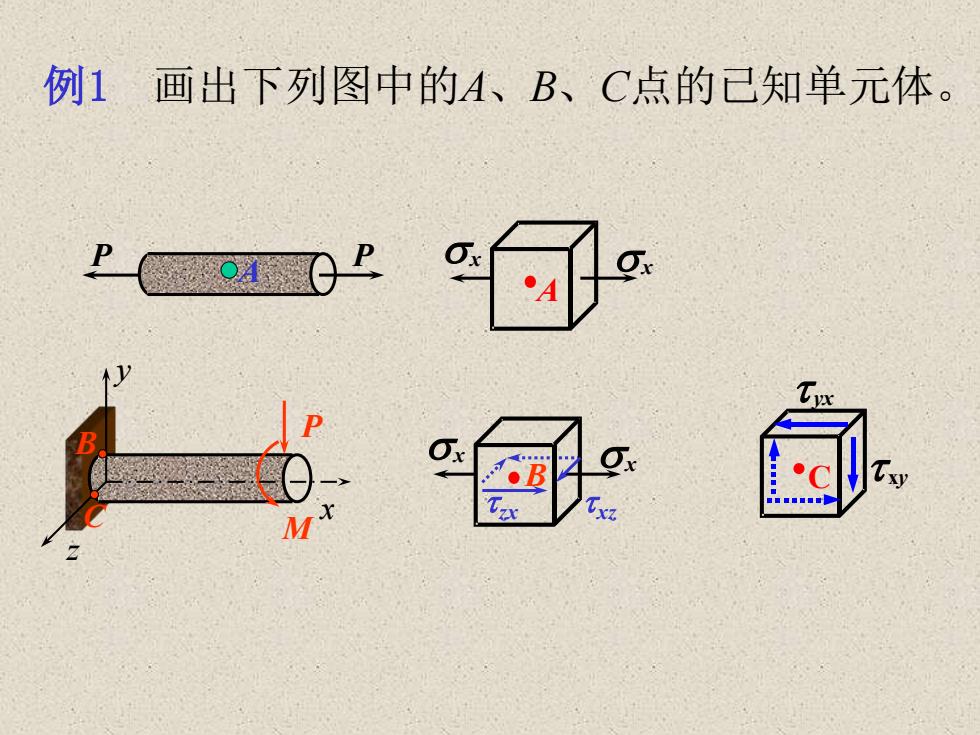
例1画出下列图中的A、B、C点的已知单元体。OxPOxTyxaxgxOB代M

zx 例1 画出下列图中的A、B、C点的已知单元体。 P P A A  x x M P x y z B C  x x B  xz C  xy  yx

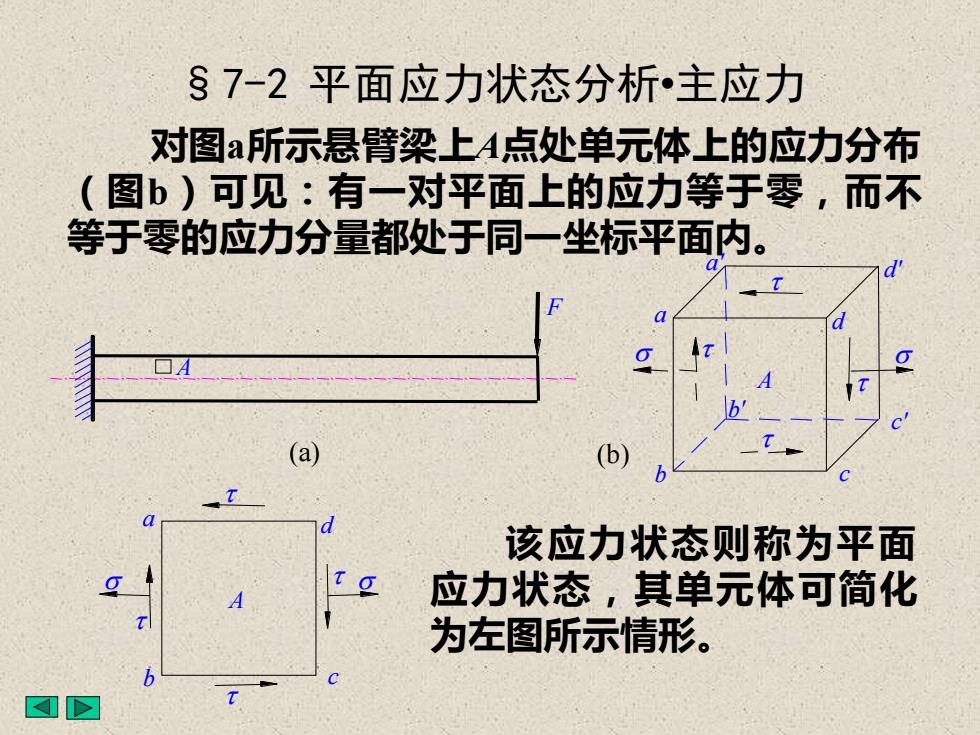
S7-2平面应力状态分析·主应力对图a所示悬臂梁上A点处单元体上的应力分布（图b）可见：有一对平面上的应力等于零，而不等于零的应力分量都处于同一坐标平面内。该应力状态则称为平面O应力状态，其单元体可简化为左图所示情形

§7-2 平面应力状态分析•主应力 对图a所示悬臂梁上A点处单元体上的应力分布 （图b）可见：有一对平面上的应力等于零，而不 等于零的应力分量都处于同一坐标平面内。       A F (a) a d b c A a' b' d' c' (b) a d b c A       该应力状态则称为平面 应力状态，其单元体可简化 为左图所示情形

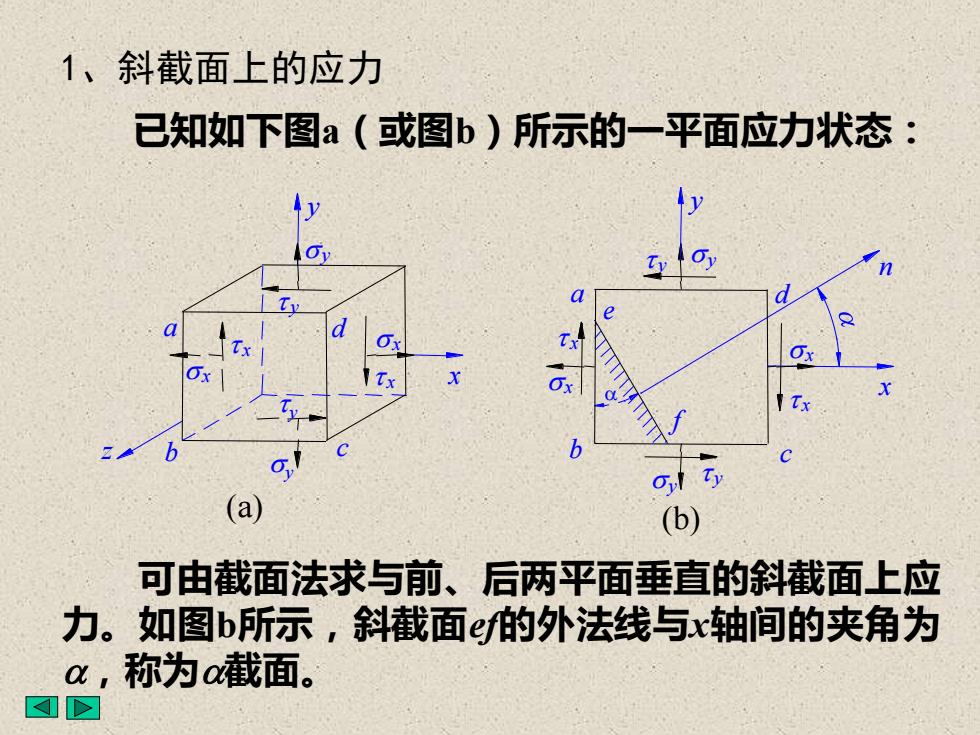
1、斜截面上的应力已知如下图a（或图b）所示的一平面应力状态：Oylty(a)(b)可由截面法求与前、后两平面垂直的斜截面上应力。如图b所示，斜截面e的外法线与x轴间的夹角为α，称为α截面。A

1、斜截面上的应力 已知如下图a（或图b）所示的一平面应力状态： e f a n x y z a b c d  x  y (a) x y  y y x  x a d b c  x  y  x x (b) x x y y  y y 可由截面法求与前、后两平面垂直的斜截面上应 力。如图b所示，斜截面ef的外法线与x轴间的夹角为 a，称为a截面

应力的正负和斜截面夹角的正负规定：1）正应力o拉为正，压为负；2）切应力使单元体产生顺时针旋转趋势为正：反之为负；3）对α角，x轴逆时针旋转这一角度而与斜截面外法线重合时，其值为正；反之为负。取图c所示分离体进行分析。图c中所示斜截面上应力和斜截面夹角均为正。(c)

应力的正负和斜截面夹角的正负规定： 1）正应力拉为正，压为负； 2）切应力使单元体产生顺时针旋转趋势为正；反之 为负； 3）对a角，x轴逆时针旋转这一角度而与斜截面外法 线重合时，其值为正；反之为负。 取图c所示分离体进行分析。图c中所示斜截面 上应力和斜截面夹角均为正。 e f b y x a a (c) x y

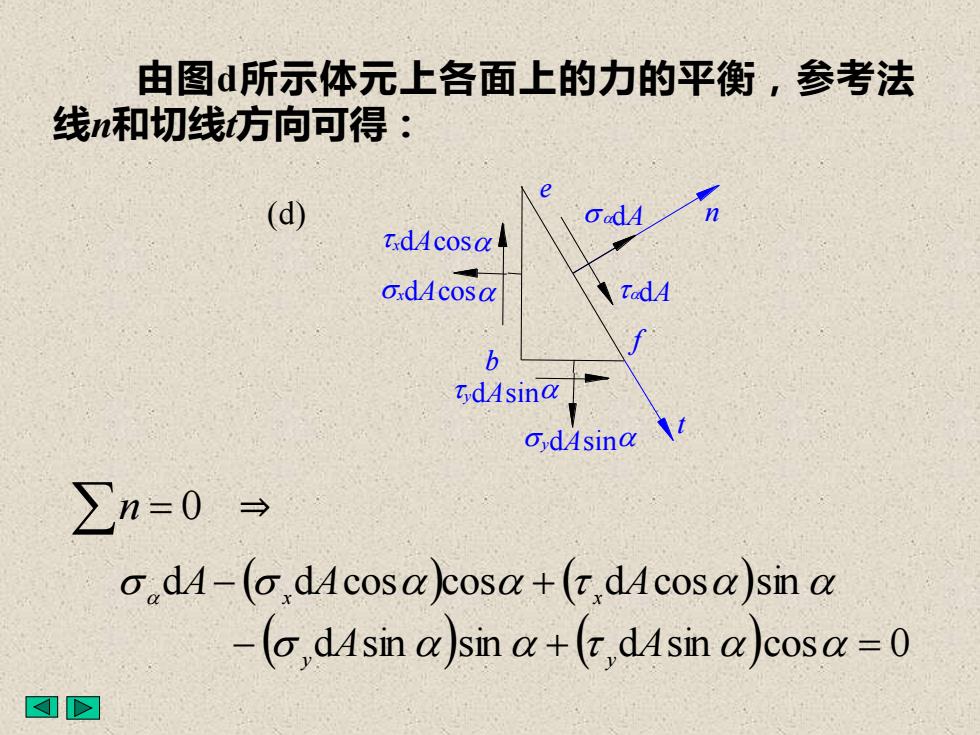
由图d所示体元上各面上的力的平衡，参考法线n和切线方向可得：(d)CadAt.dAcosαo.dAcosaTadAbtdAsinao,dAsinaIn=0 =o.dA-(o,dAcosα)cosα+ (t,dAcosα)sin α- (,dAsin α)sin α + (t,dAsin α)cosα = 0

n = 0 ( ) ( ) ( d sin )sin ( d sin )cos 0 d d cos cos d cos sin − + = − +  a a  a a  a  a a  a a A A A A A y y x x 由图d所示体元上各面上的力的平衡，参考法 线n和切线t方向可得： ⇒ n t ydAsina (d) b f ydAsina adA xdAcosa e  adA xdAcosa

Zt=0-t,dA-(α dAcosα)sin α-(t,dAcosα)cosα+ (α,dAsin α)cosα+ (t,dAsin α)sin α = 0其中dA为斜截面e的面积由此可得，任一斜截面上的应力分量为：O,+oyOx-oycos 2α-t, sin 2α0220x-0,sin 2α + t, cos 2α22

a  a      a cos 2 sin 2 2 2 x x y x y − − + + = 由此可得，任一斜截面上的应力分量为： t = 0 ( ) ( ) ( d sin )cos ( d sin )sin 0 d d cos sin d cos cos + + = − −  a a  a a  a  a a  a a A A A A A y y x x ⇒ 其中dA为斜截面ef的面积。 a  a    a sin 2 cos 2 2 x x y + − =

例7-1图示圆轴中，已知：圆轴直径d-100mm，轴向拉力F=500kN，外力矩M.=7kN·m。求C点α=-30°截面上的应力。V口Ca.OT.7(a)(b)解：C点应力状态如图b所示，其拉应力和切应力为：F500×103=63.7MPax元A元×10024

解：C点应力状态如图b所示，其拉应力和切应力为： 63.7MPa 100 4 π 500 10 2 3 =   = = A F  x 例7-1 图示圆轴中，已知：圆轴直径d=100mm，轴向 拉力F=500kN，外力矩Me =7kN·m。求C点a =−30°截 面上的应力。 (b) C x  x x x  x  y  y y (a) x T F T C F