内蒙古科技大学：《材料力学》课程PPT教学课件（机械类）第五章 弯曲应力

第五章弯曲应力目录

第五章 弯曲应力 目录

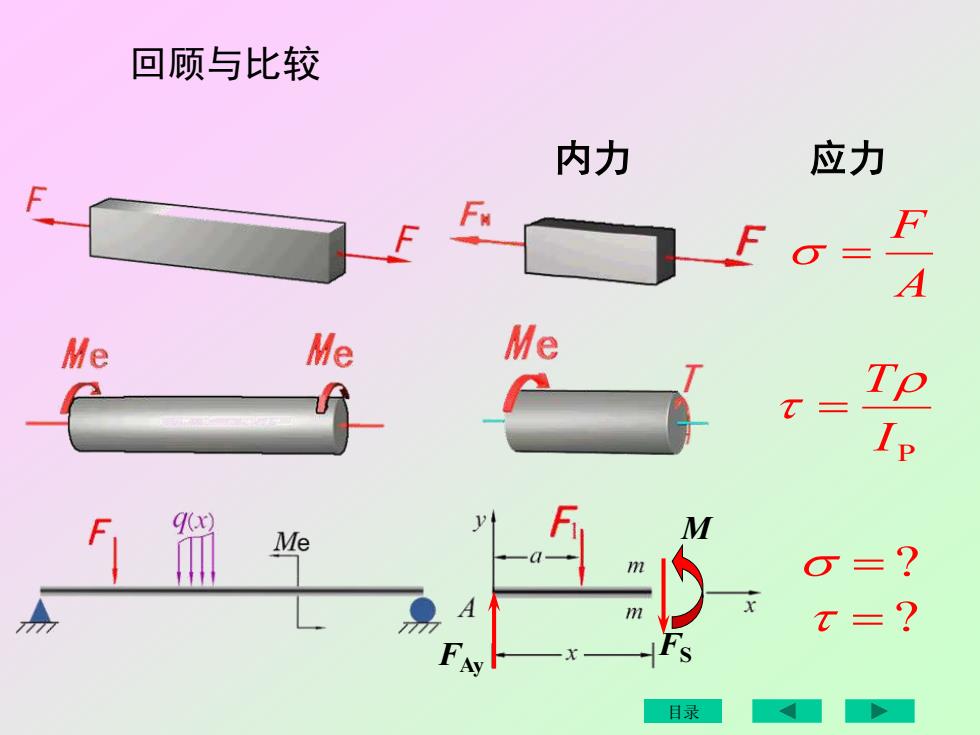
回顾与比较应力内力F-AMeMeMe福MMe?mm2目录

回顾与比较 内力 A F  = 应力 P I T  = FAy FS M  = ?  = ? 目录

dA-odAtdAαdA= MtdA =FTF9介M在横截面上，只有法向内力元素cdA才能合成弯矩M，只有切向内力元素tdA才能合成剪力F

在横截面上，只有法向内力元素σdA才能合成 弯矩M，只有切向内力元素τdA才能合成剪力  dA  dA  M dA  dA dA Fs    M  Fs  Fs

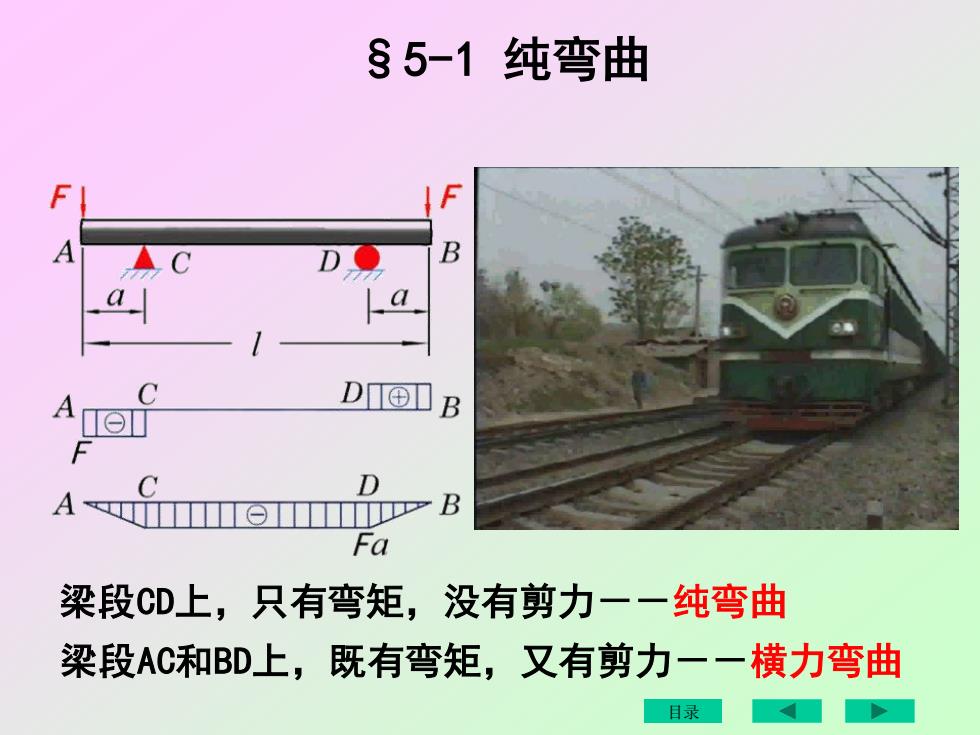
s 5-1 纯弯曲FAB广aDOBCATODfALOIBFa梁段CD上，只有弯矩，没有剪力一一纯弯曲横力弯曲梁段AC和BD上，既有弯矩，又有剪力一一目录A

梁段CD上，只有弯矩，没有剪力－－纯弯曲 梁段AC和BD上，既有弯矩，又有剪力－－横力弯曲 §5-1 纯弯曲 目录

纯弯曲时梁横截面上的正应力85-24变形几何关系从三方面考虑：物理关系静力学关系、变形几何关系用较易变形的材料制成的矩形截面等直梁作纯弯曲试验：

§5-2 纯弯曲时梁横截面上的正应力 从三方面考虑： 一、变形几何关系 用较易变形的材料制成的矩形截面等直梁 作纯弯曲试验: 变形几何关系 物理关系 静力学关系

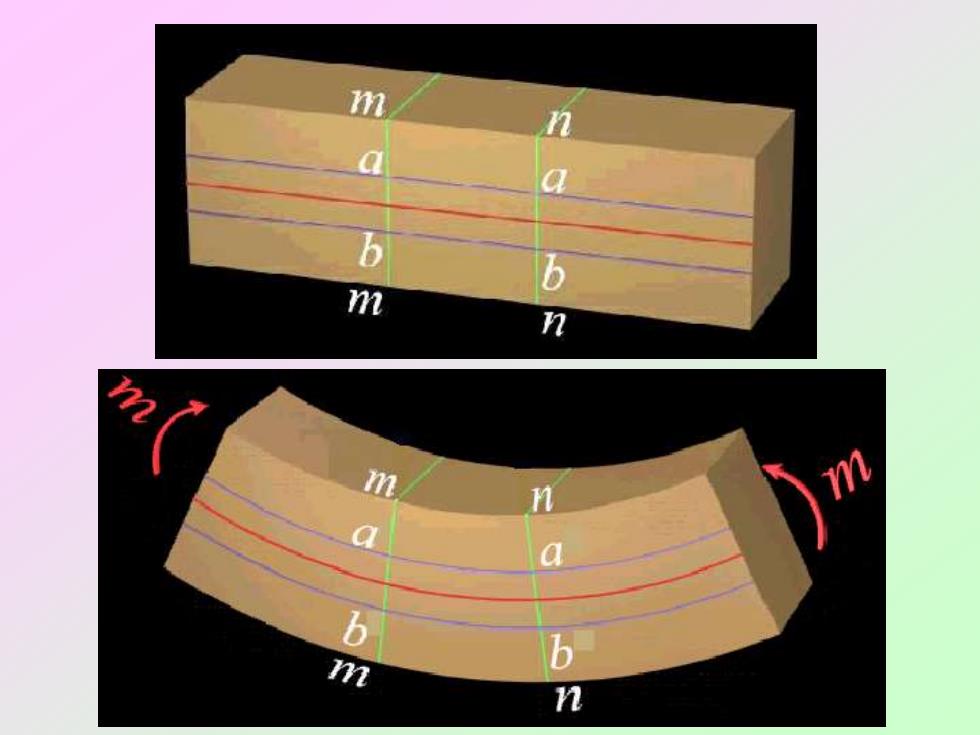
mnaab6mn2mnQa6bmn

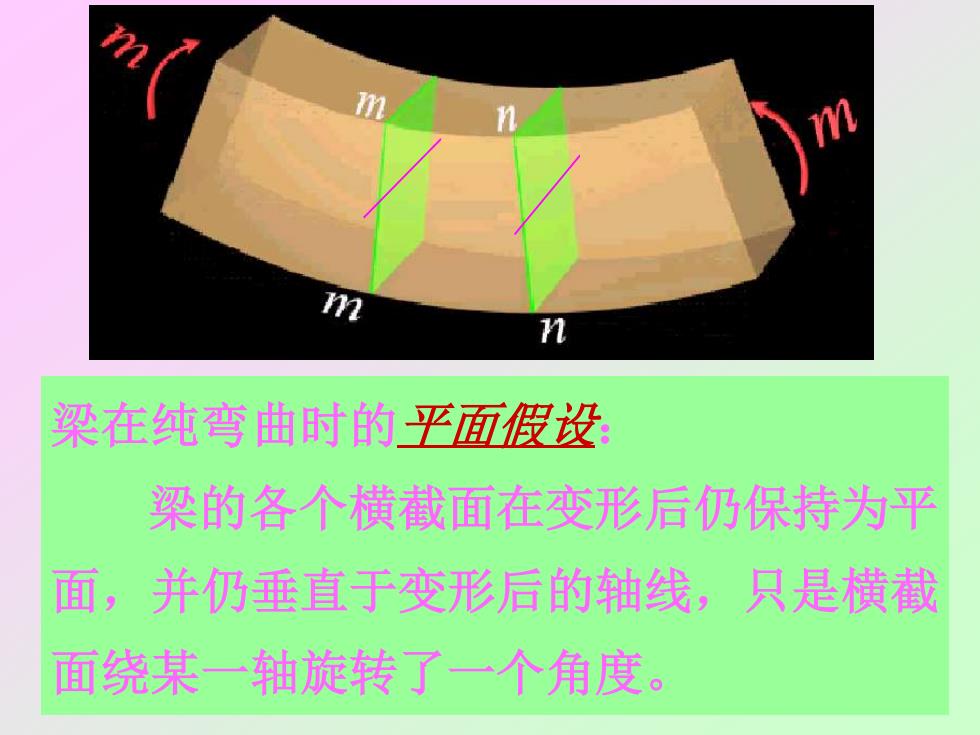
m门Nmn梁在纯弯曲时的平面假设梁的各个横截面在变形后仍保持为平面，并仍垂直于变形后的轴线只是横截面绕某一轴旋转了一个角度

梁在纯弯曲时的平面假设： 梁的各个横截面在变形后仍保持为平 面，并仍垂直于变形后的轴线，只是横截 面绕某一轴旋转了一个角度

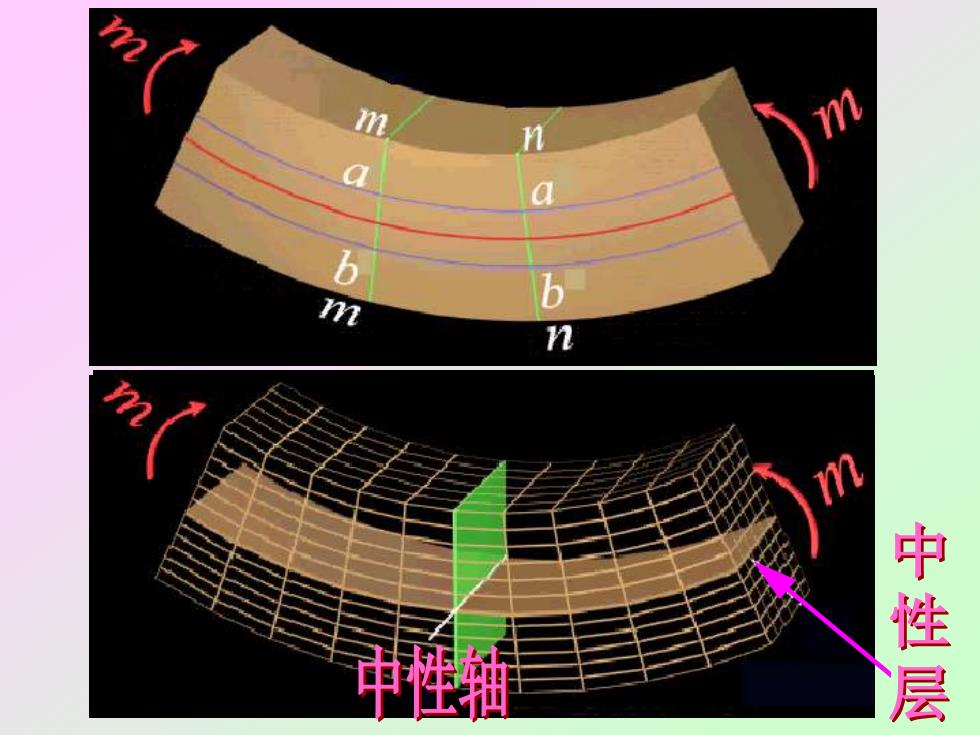
mmH?a6bmn元N中性层中性轴

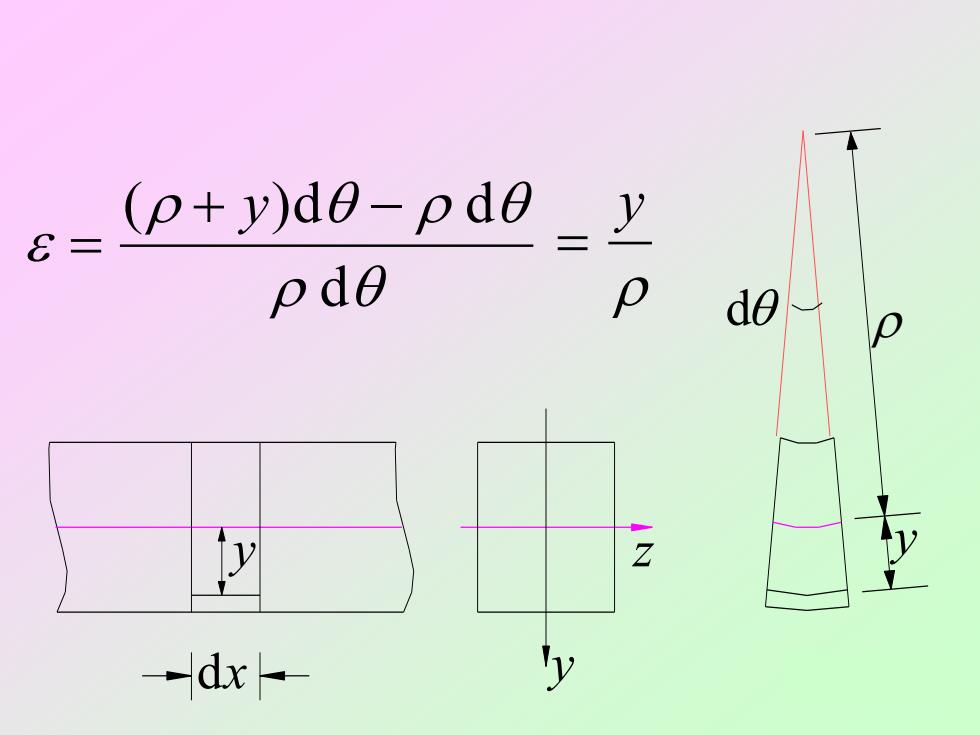
(p+y)de-pdeJ8pdepdeO1ydx←

       = ( + y)d − d d y CL8TU3-2 z dx y d y  = y 

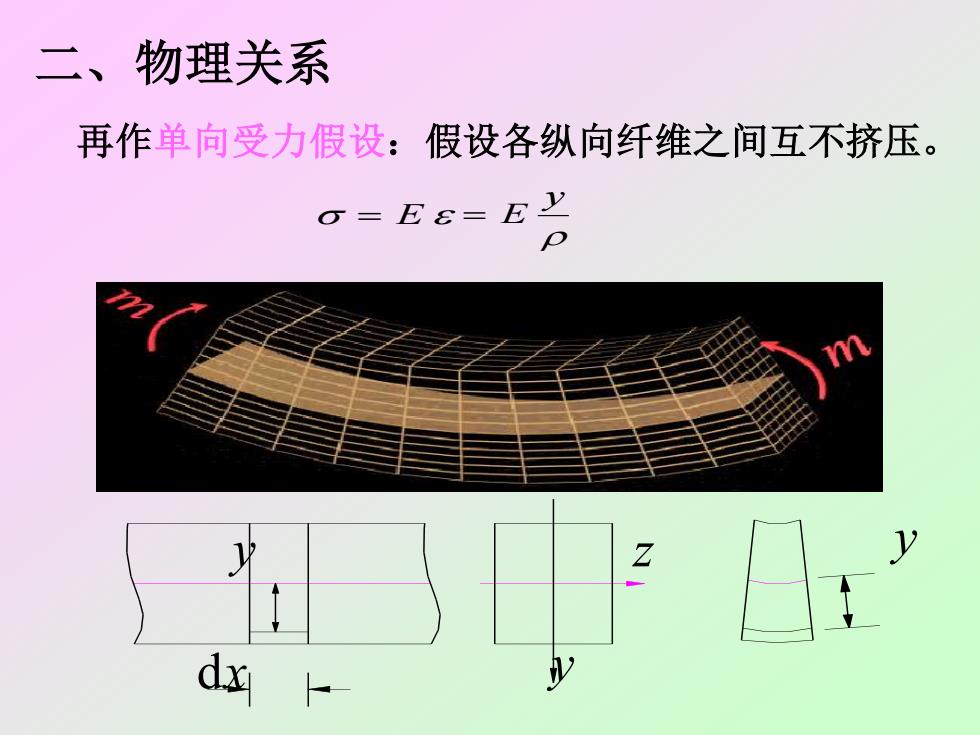
二、物理关系再作单向受力假设：假设各纵向纤维之间互不挤压。=E6=Ep1dxiV

二、物理关系  = E  = E y  y z dx y y 再作单向受力假设：假设各纵向纤维之间互不挤压