
复变函数第四节几个初等函数所构成的映射一、幂函数二、指数函数三、儒可夫斯基函数四、小结与思考U
第四节 几个初等函数所构成 的映射 一、幂函数 二、指数函数 三、儒可夫斯基函数 四、小结与思考

复变函数一、幂函数 w= z"(n≥2为自然数)该函数在z平面内处处可导,导数dw-=nzdz.(1)当z±0时:dw≠0.则在z平面内除原点外dz由w=zn所构成的映射是处处共形的u
2 一、幂函数 w = z (n 2为自然数) n 1 d d − = n nz z w (1)当z 0时 : 0, , d d 则在z平面内除原点外 z w 由 所构成的映射是处处共形的. n w = z 该函数在z平面内处处可导,导数

复变函数(2)当z =0时:令z= reio,W=peig,有p=r",Φ= ng.则:1)圆周z= r圆周w= rn(特殊地:单位圆周映射为单位圆周)射线=n2)射线0=0(正实轴θ=0映射成正实轴@=0)u
3 (2)当z = 0时 : , , i i 令 z = re w = e r , n . n 有 = = 则: 1) 圆周 z = r n 圆周w = r (特殊地: 单位圆周映射为单位圆周) 射线 = 0 射线 = n 0 (正实轴 = 0映射成正实轴 = 0) 2)
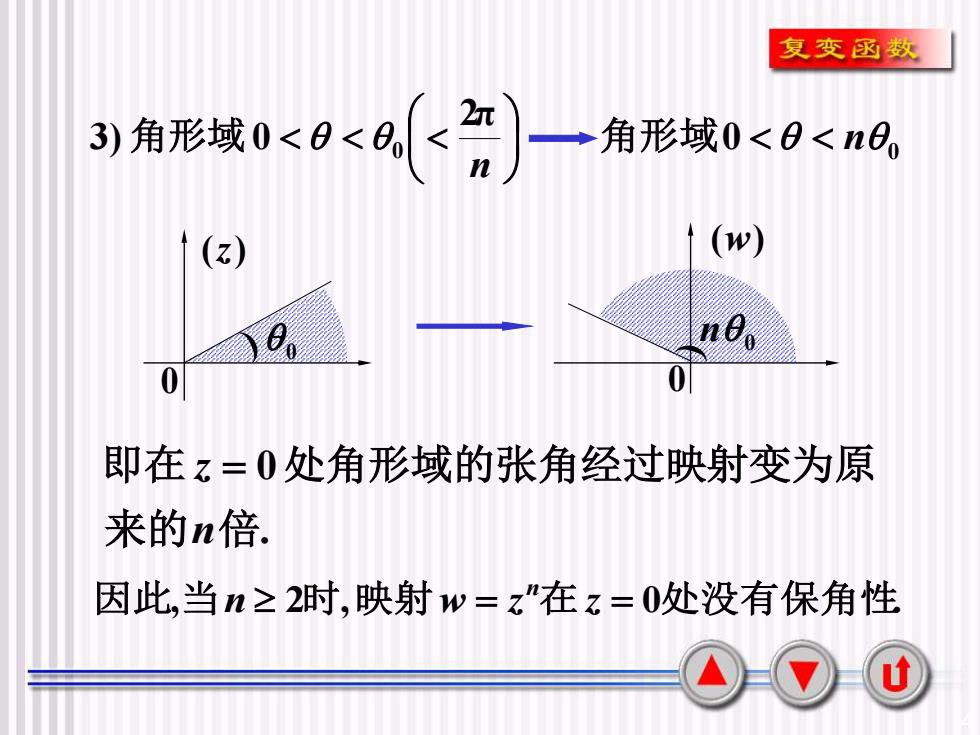
复变函数2()一3)角形域0<0<(角形域0<<n(w)(z)ne.0.00即在z=0处角形域的张角经过映射变为原来的n倍。因此,当n≥2时,映射w = z"在z= 0处没有保角性u
4 2π 3) 0 0 n 角形域 角形域0 n 0 . 0 来的 倍 即在 处角形域的张角经过映射变为原 n z = 0 n 0 0 (w) 0 (z) 因此,当n 2时,映射w = z 在 z = 0处没有保角性. n
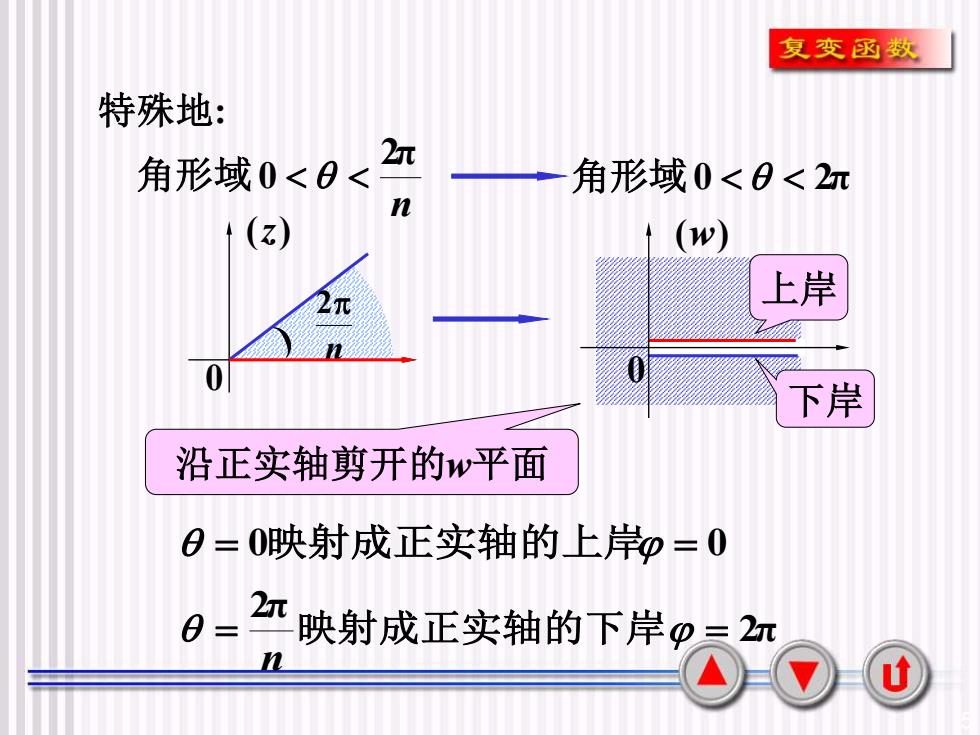
复变函数特殊地:2元角形域0<θ角形域0<θ<2元n(z)(w)上岸2元0下岸沿正实轴剪开的w平面θ=0映射成正实轴的上岸β=02元0=映射成正实轴的下岸@2元nU
5 0 (z) 特殊地: 2π 0 n 角形域 角形域0 2π n 2 = 0映射成正实轴的上岸 = 0 2π 2π = 映射成正实轴的下岸 = n 上岸 (w) 0 沿正实轴剪开的w平面 下岸
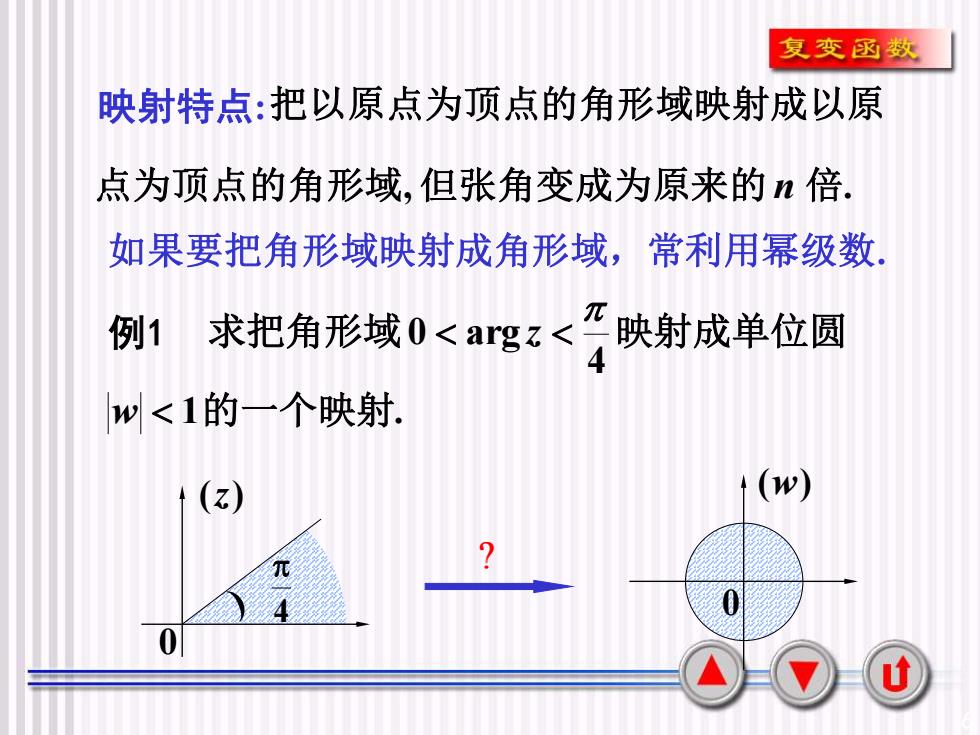
复变函数映射特点:把以原点为顶点的角形域映射成以原点为顶点的角形域,但张角变成为原来的n倍如果要把角形域映射成角形域,常利用幂级数元例1 映射成单位圆求把角形域0<argz<一4w<1的一个映射(w)(z)元80u
6 映射特点:把以原点为顶点的角形域映射成以原 点为顶点的角形域, 但张角变成为原来的 n 倍. 4 求把角形域0 arg 映射成单位圆 z w 1的一个映射. 0 (z) 4 ? 0 (w) 如果要把角形域映射成角形域,常利用幂级数. 例1
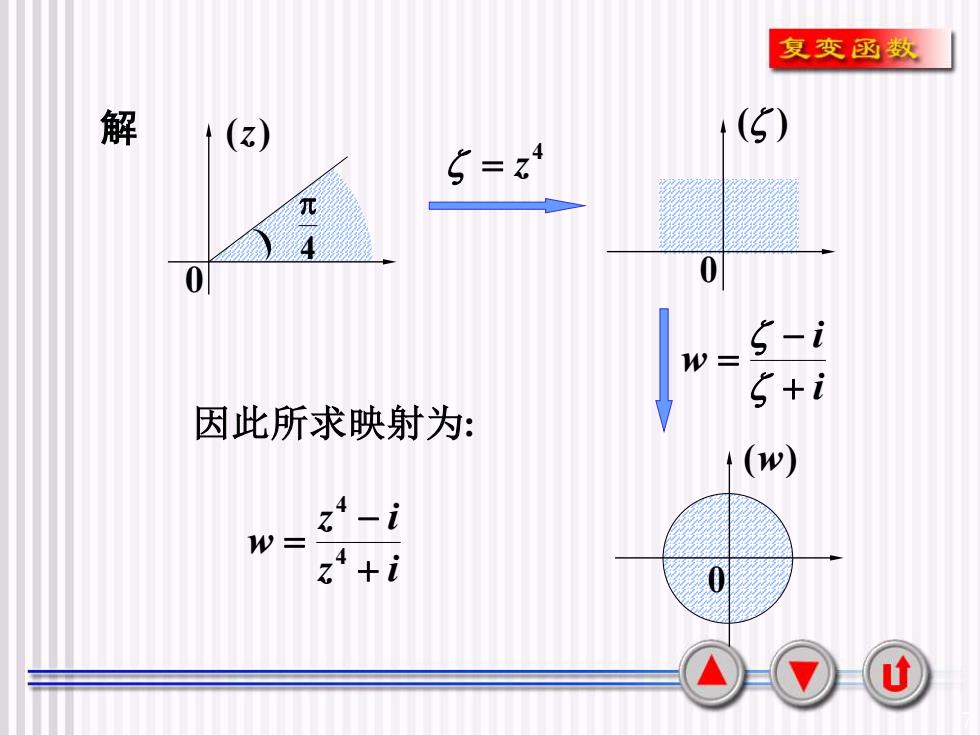
复变函数(5)解 (z)=Z元400S-iW=S+i因此所求映射为:(w)z4-iW=4z*+i0U
7 解 4 = z i i w + − = z i z i w + − = 4 4 0 (z) 4 0 (w) 0 ( ) 因此所求映射为:
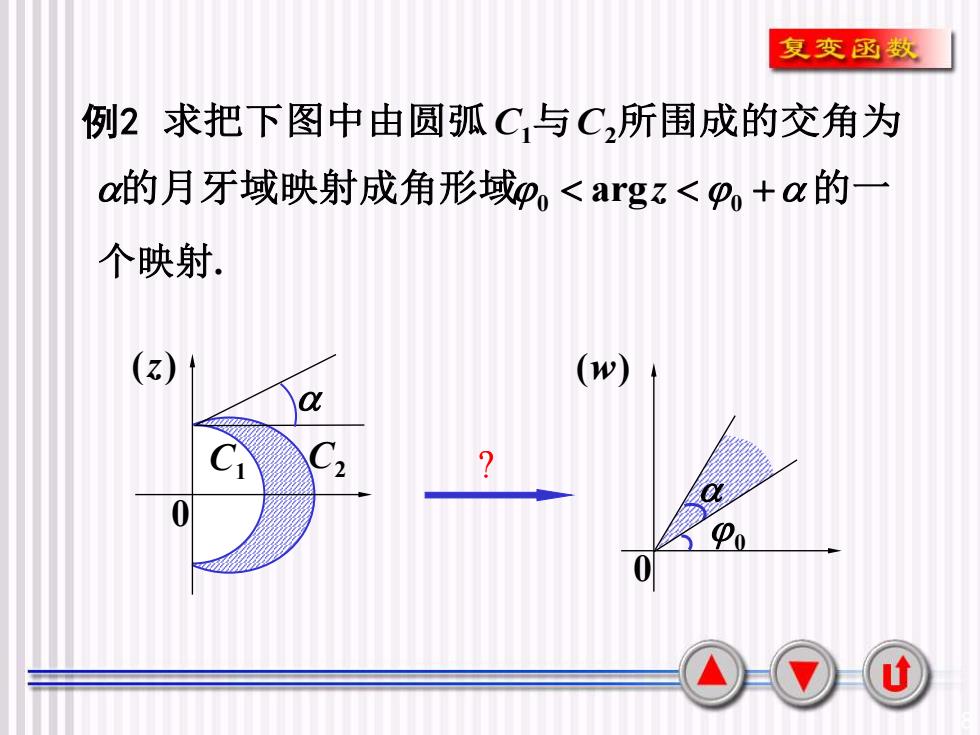
复变函数例2 求把下图中由圆弧C,与C,所围成的交角为α的月牙域映射成角形域po<argz<P+α的一个映射.(z)(w)αSC17o0Po0u
8 C 1 C2 0 ( z ) 求把下图中由圆弧C1与C2所围成的交角为 的月牙域映射成角形域0 argz 0 + 的一 个映射 . 0 ( w ) 0 ? 例 2
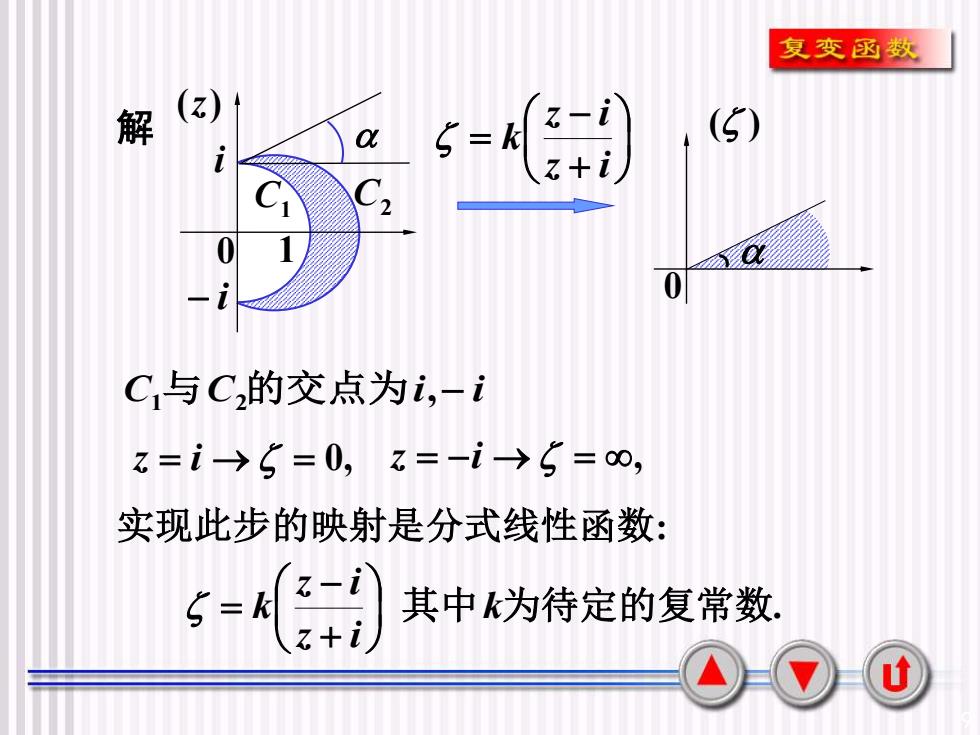
复变函数(z)z-i()解S= kα二z+iCC10101一C,与C,的交点为i,一 iz=i→=0, z=-i→=0,实现此步的映射是分式线性函数:z-i其中k为待定的复常数S=kz+iU
9 0 ( ) 解 − i C1 C2 0 (z) 1 , 1 2 C 与C 的交点为i − i z = i → = 0, z = −i → = , i 实现此步的映射是分式线性函数: 其中k为待定的复常数. z i z i k + − = + − = z i z i k
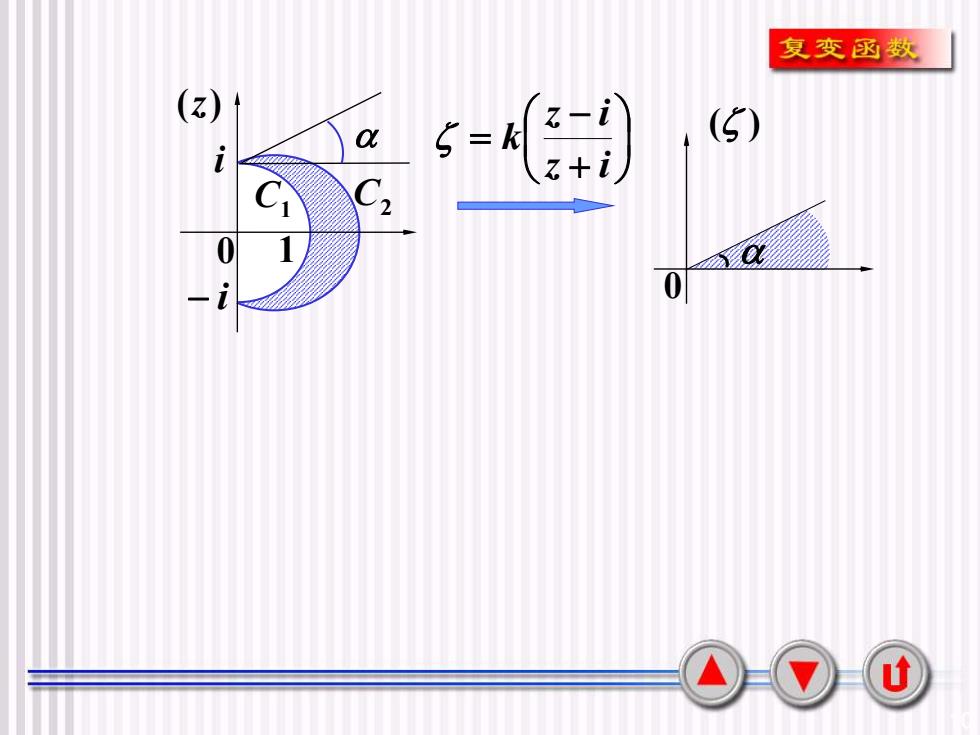
复变函数(z)z-i()=kSαz+iCC10120-U
10 0 ( ) − i C1 C2 0 ( z ) 1 i +− = z i z i k