《复变函数与积分变换》课程教学资源（PPT课件）第三章 复变函数的积分 3.3 第三节 基本定理的推广——复合闭路定理

复变函数第三节 基本定理的推广复合闭路定理一、问题的提出二、复合闭路定理三、典型例题四、小结与思考U

第三节 基本定理的推广 一、问题的提出 二、复合闭路定理 三、典型例题 复合闭路定理 四、小结与思考

复变函数问题的提出一、实例，计算dz.Jz=2 z 1因为z=2是包含z=1在内的闭曲线根据本章第一节例4可知，dz = 2元i.Jz/=2 z -1由此希望将基本定理推广到多连域中1

2 一、问题的提出  =2 − d . 1 1 , z z z 实例 计算 因为 z = 2是包含z = 1在内的闭曲线, 根据本章第一节例4可知,  = =  2 − d 2 . 1 1 z z i z 由此希望将基本定理推广到多连域中

复变函数二、复合闭路定理1.闭路变形原理设函数 f(z)在多连通域内解析C 及C,为D内的任意两条简单闭曲线(正向为逆时针方向)AIABCBC 及C, 为边界的区域DDiD全含于D.作两段不相交的弧段AA' 和 BB'U

3 二、复合闭路定理 1. 闭路变形原理 设函数 f (z)在多连通域内解析, ( ), 1 单闭曲线 正向为逆时针方向 C 及C 为 D内的任意两条简 . 1 1 D C C D 全含于 及 为边界的区域 D C C1 D1 A A B B 作两段不相交的弧段 AA和 BB , ︵ ︵

复变函数为了讨论方便添加字符E,E,F,F'显然曲线AEBB'EA'A,AA'F'B'BFA均为封闭曲线因为它们的内部全含于D故S f(z)dz = 0,AEBB'E'A'AB f(z)dz = 0.DDAA'F'B'BFAAEBB'E'A'A = AEB + BB' + B'E'A' +AAAA'F'B'BFA = AA' +A'F'B' + B'B + BFAU

4 D C C1 D1 A A B B E E F F 显然曲线AEBBEAA, AAFBBFA 为了讨论方便,添加字符E, E , F, F , 均为封闭曲线. 因为它们的内部全含于D, ( )d = 0,  AEBBEAA 故 f z z ( )d = 0.  AAFBBFA f z z AEBBEAA = AEB + BB + BEA + AA, ︵ ︵ ︵ ︵ AAFBBFA = AA + AFB + BB + BFA, ︵ ︵ ︵ ︵

复变函数由f f(z)dz + f(z)dz = 0, 得AEBB'E'AAAA'F'B'BFAff(z)dz + ff(z)dz+ ff(z)dz+ ff(z)dzAA'C1f f(z)dz + f f(z)dz = 0,+ABBBB'BD即f f(z)dz + f f(z)dz = 0,CC1或f f(z)dz = f f(z)dz.CCiu

5  AEBBEAA 由 f (z)dz + ( )d = 0,  AAFBBFA f z z 得 D C C1 D1 A A B B E E F F  C f (z)dz  − + 1 ( )d C f z z   + AA f (z)dz ︵   + A A f (z)dz ︵ + ( )d = 0,  BB f z z ︵   + B B f (z)dz ︵ ( )d ( )d 0, 1 + =   − C C 即 f z z f z z ( )d ( )d . 1   = C C 或 f z z f z z

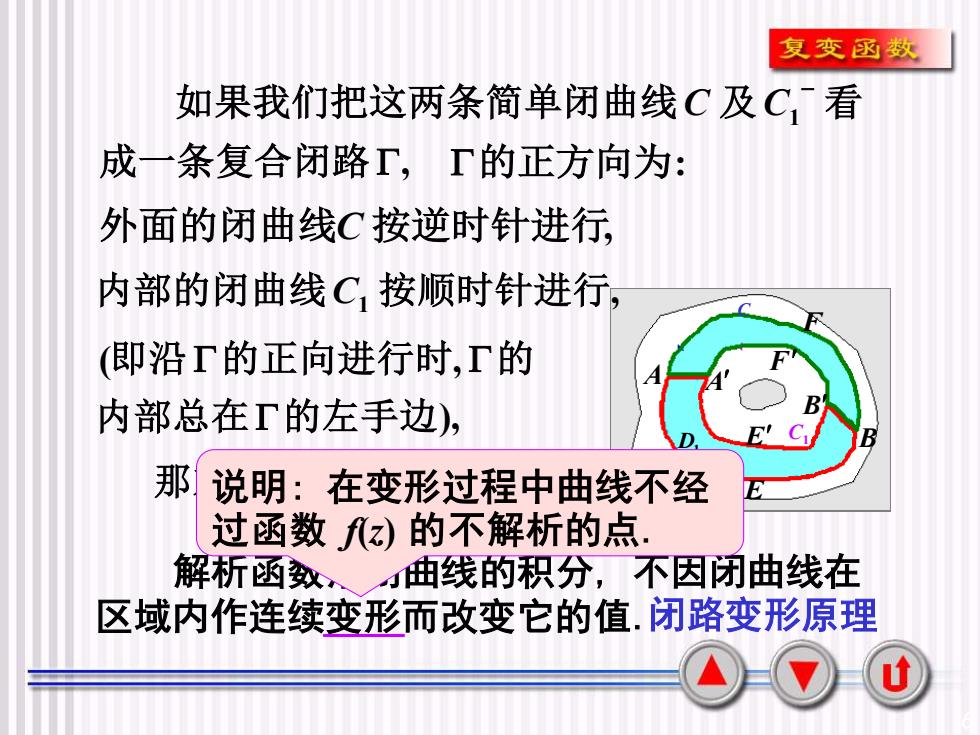
复变函数如果我们把这两条简单闭曲线C及C-看成一条复合闭路I，「的正方向为外面的闭曲线C按逆时针进行内部的闭曲线C,按顺时针进行(即沿I的正向进行时,I的R内部总在I的左手边)那说明：在变形过程中曲线不经A过函数z）的不解析的点解析函数，曲线的积分，不因闭曲线在区域内作连续变形而改变它的值.闭路变形原理u

6 D C C1 D1 A A B B E E F F , 1  − 成一条复合闭路 如果我们把这两条简单闭曲线C 及C 看 的正方向为: 外面的闭曲线C 按逆时针进行, , 内部的闭曲线C1 按顺时针进行 ), ( , 内部总在 的左手边 即沿 的正向进行时 的    ( ) = 0.   那末 f z dz 解析函数沿闭曲线的积分, 不因闭曲线在 区域内作连续变形而改变它的值.闭路变形原理 说明: 在变形过程中曲线不经 过函数 f(z) 的不解析的点

复变函数2.复合闭路定理设C为多连通域D内的一条简单闭曲线C,C2，C，是在C内部的简单闭曲线它们互不包含也互不相交并且以C,C1,C2··",C,为边界的区域全含于D如果,f(z)在D内解析C3C那末DZf(1)f (z)dz =)f(z)dz,JCk=1L其中C及C.均取正方向u

7 2. 复合闭路定理 , , , , , , , , , , , 1 2 1 2 D C C C C C C C C C D n n 为边界的区域全含于 互不包含也互不相交并且以 是 在 内部的简单闭曲线它 们 设 为多连通域 内的一条简单闭曲线   如果 f (z)在 D内解析, D C C1 C2 C3 那末 (1) ( )d ( )d , 1   = = n k C C k f z z f z z 其中 及 均取正方向; C Ck

复变函数(2) f f(z)dz = 0.这里I为由C,C1,C2,,C,组成的复合闭路(其方向是：C按逆时针进行,Ci,C2,C,按顺时针进行

8 D C C1 C2 C3 (2) ( )d = 0.   f z z ). ( : , , , , , , , , 1 2 1 2 顺时针进行 其方向是 按逆时针进行 按 这 里 为 由 组成的复合闭路 n n C C C C C C C C   

复变函数三、典型例题2z-1例1计算积分dz,I为包含圆周z=122-zJ斤在内的任何正向简单闭曲线2z-1解因为函数在复平面2Z"-Z+x内有两个奇点z=0和z=1,T依题意知，也包含这两个奇点u

9 三、典型例题 例1 解 . d , 1 2 1 2 在内的任何正向简单闭曲线 计算积分  为包含圆周   = − − z z z z z 0 1, 2 1 2 = = − − z z z z z 内有两个奇点 和 因为函数 在复平面 依题意知, x y o • • 1  也包含这两个奇点， 

复变函数在工内作两个互不包含也互不相交的正向圆周CI 和C2'Cl只包含奇点z=0.C2只包含奇点z=1，根据复合闭路定理2z-1 dzfd-2z-1dz +01227Z7-ZCC2x+d+fd++d+fddzI=0+2元i+2元i+0=4元iU

10 , C1 和C2 在内作两个互不包含也互不相交的正向圆周 x y o • • 1  0, C1 只包含奇点 z = 1, C2 只包含奇点 z = C1 C2 根据复合闭路定理, = − −   z z z z d 2 1 2   − − + − − 1 2 d 2 1 d 2 1 2 2 C C z z z z z z z z     + − + + − = 1 1 2 2 d 1 d 1 1 d 1 d 1 1 C C C C z z z z z z z z = 0 + 2i + 2i + 0 = 4i