
第三章原子结构和元素周期表 3.1原子核外电子的运动状态 一、玻尔的原子结构理论 1913年,丹麦青年物理学家玻尔(N.Bohhr)在氢原子光谱和普朗克(M.Planck)量子 理论的基础上提出了如下假设: ()原子中的电子只能沿着某些特定的、以原子核为中心、半径和能量都确定的轨 道上运动,这些轨道的能量状态不随时间而改变,称为稳定轨道(或定态轨道)。 (2)在一定轨道中运动的电子具有一定的能量,处在稳定轨道中运动的电子,既不 吸收能量,也不发射能量。电子只有从一个轨道跃迁到另一轨道时,才有能量的吸收和 放出。在离核越近的轨道中,电子被原子核束缚越牢,其能量越低;在离核越远的轨道 上,其能量越高。轨道的这些不同的能量状态,称为能级。轨道不同,能级也不同。在 正常状态下,电子尽可能处于离核较近、能量较低的轨道上运动,这时原子所处的状态 称为基态,其余的称为激发态。 (③)电子从一个定态轨道跳到另一个定态轨道,在这过程中放出或吸收能量,其频 率与两个定态轨道之间的能量差有关。 二、电子的波粒二象性 光的干涉、衍射等现象说明光具有波动性:而光电效应、光的发射、吸收又说明光 具有粒子性。因此光具有波动和粒子两重性,称为光的波粒二象性。 光的波粒二象性启发了法国物理学家德布罗意(de Brog1ie),1924年,他提出了一 个大胆的假设:认为微观粒子都具有波粒二象性:也就是说,微观微粒除具有粒子性外, 还具有波的性质,这种波称为德布罗意波或物质波。1927年,德布罗意的假设经电子衍 射实验得到了完全证实。美国物理学家戴维逊(C.J.Davisson)和革末(L.H.Ge rmer)进 行了电子衍射实验,当将一束高速电子流通过镍晶体(作为光橱)而射到荧光屏上时,结 果得到了和光衍射现象相似的一系列明暗交替的衍射环纹,这种现象称为电子衍射。衍 射是一切波动的共同特征,由此充分证明了高速运动的电子流,也具有波粒二象性。除 光子、电子外,其他微观粒子如:质子、中子等也具有波粒二象性。 这种具有波粒二象性的微观粒子,其运动状态和宏观物体的运动状态不同。例如, 导弹、人造卫星等的运动,它在任何瞬间,人们都能根据经典力学理论,准确地同时测 定它的位置和动量:也能精确地预测出它的运行轨道。但是像电子这类微观粒子的运动
1 第三章 原子结构和元素周期表 3.1 原子核外电子的运动状态 一、玻尔的原子结构理论 1913 年,丹麦青年物理学家玻尔(N.Bohhr)在氢原子光谱和普朗克(M.Planck)量子 理论的基础上提出了如下假设: (1)原子中的电子只能沿着某些特定的、以原子核为中心、半径和能量都确定的轨 道上运动,这些轨道的能量状态不随时间而改变,称为稳定轨道(或定态轨道)。 (2)在一定轨道中运动的电子具有一定的能量,处在稳定轨道中运动的电子,既不 吸收能量,也不发射能量。电子只有从一个轨道跃迁到另一轨道时,才有能量的吸收和 放出。在离核越近的轨道中,电子被原子核束缚越牢,其能量越低;在离核越远的轨道 上,其能量越高。轨道的这些不同的能量状态,称为能级。轨道不同,能级也不同。在 正常状态下,电子尽可能处于离核较近、能量较低的轨道上运动,这时原子所处的状态 称为基态,其余的称为激发态。 (3)电子从一个定态轨道跳到另一个定态轨道,在这过程中放出或吸收能量,其频 率与两个定态轨道之间的能量差有关。 二、电子的波粒二象性 光的干涉、衍射等现象说明光具有波动性;而光电效应、光的发射、吸收又说明光 具有粒子性。因此光具有波动和粒子两重性,称为光的波粒二象性。 光的波粒二象性启发了法国物理学家德布罗意(de Broglie),1924 年,他提出了一 个大胆的假设:认为微观粒子都具有波粒二象性;也就是说,微观微粒除具有粒子性外, 还具有波的性质,这种波称为德布罗意波或物质波。1927 年,德布罗意的假设经电子衍 射实验得到了完全证实。美国物理学家戴维逊(C.J.Davisson)和革末(L.H.Ge rmer) 进 行了电子衍射实验,当将一束高速电子流通过镍晶体(作为光栅)而射到荧光屏上时,结 果得到了和光衍射现象相似的一系列明暗交替的衍射环纹,这种现象称为电子衍射。衍 射是一切波动的共同特征,由此充分证明了高速运动的电子流,也具有波粒二象性。除 光子、电子外,其他微观粒子如:质子、中子等也具有波粒二象性。 这种具有波粒二象性的微观粒子,其运动状态和宏观物体的运动状态不同。例如, 导弹、人造卫星等的运动,它在任何瞬间,人们都能根据经典力学理论,准确地同时测 定它的位置和动量;也能精确地预测出它的运行轨道。但是像电子这类微观粒子的运动

由于兼具有波动性,人们在任何瞬间都不能准确地同时测定电子的位置和动量:它也没 有确定的运动轨道。所以在研究原子核外电子的运动状态时,必须完全摒弃经典力学理 论,而代之以描述微观粒子运动的量子力学理论。 三、波函数与原子轨道 l926年奥地利物理学家薛定谔(伦.Schrodinger)把电子运动帮光的波动性理论联系 起来,提出了描述核外电子运动状态的数学方程,称为薛定谔方程。薛定谔方程把作为 粒子物质特征的电子质量(m)、位能(W)和系统的总能量(E)与其运动状态的波函数0列 在一个数学方程式中,即体现了波动性和粒子性的结合。解薛定谔方程的目的就是求出 波函数以及与其相对应的能量E,这样就可了解电子运动的状态和能量的高低。求得 (x,y,z)的具体函数形式,即为方程的解。它是一个包含三个常数项、1、m和三个变 量x、y、z的函数式。 从理论上讲,通过解薛定谔方程可得出波函数,但薛定谔方程的许多解在数学上是 合理的,且运算极为复杂,只有满足特定条件的解才有物理意义,用来描述核外电子运 动状态。为了得到描述电子运动状态的合理解,必须对三个参数、1、m按一定的规律 取值。这三个函数,分别称为主量子数、角量子数和磁量子数 求解方程得出的不是一个具体数值,而是用空间坐标(x,y,z)来描述波函数的数学 函数式,一个波函数就表示原子核外电子的一种运动状态并对应一定的能量值,所以波 函数也称原子轨道。但这里所说的原子轨道和宏观物体固定轨道的含义不同,它只是反 映了核外电子运动状态表现出的波动性和统计性规律。 为了方便,解方程时一般先将空间坐标(x,y,z)转换成球坐标平(:,日,中),而后把0 分解为用r表示的径向分布函数R()和仅包含角度变量和的角度分布函数YO。R为电 子与原子核间的距离,和代表角度。由于的角度分布与主量子数1无关,且1相同时 其角度分布图总是一样的。在下章讨论成键问题时,角度分布图有直接应用,故比较重 要。图3-1为某些原子轨道的角度分布图,图中的“+”、“-”号表示波函数的正、负值
2 由于兼具有波动性,人们在任何瞬间都不能准确地同时测定电子的位置和动量;它也没 有确定的运动轨道。所以在研究原子核外电子的运动状态时,必须完全摒弃经典力学理 论,而代之以描述微观粒子运动的量子力学理论。 三、波函数与原子轨道 1926 年奥地利物理学家薛定谔(E.Schrödinger)把电子运动帮光的波动性理论联系 起来,提出了描述核外电子运动状态的数学方程,称为薛定谔方程。薛定谔方程把作为 粒子物质特征的电子质量(m)、位能(V)和系统的总能量(E)与其运动状态的波函数()列 在一个数学方程式中,即体现了波动性和粒子性的结合。解薛定谔方程的目的就是求出 波函数以及与其相对应的能量 E,这样就可了解电子运动的状态和能量的高低。求得 (x,y,z)的具体函数形式,即为方程的解。它是一个包含三个常数项 n、l、m 和三个变 量 x、y、z 的函数式。 从理论上讲,通过解薛定谔方程可得出波函数,但薛定谔方程的许多解在数学上是 合理的,且运算极为复杂,只有满足特定条件的解才有物理意义,用来描述核外电子运 动状态。为了得到描述电子运动状态的合理解,必须对三个参数 n、l、m 按一定的规律 取值。这三个函数,分别称为主量子数、角量子数和磁量子数。 求解方程得出的不是一个具体数值,而是用空间坐标(x,y,z)来描述波函数的数学 函数式,一个波函数就表示原子核外电子的一种运动状态并对应一定的能量值,所以波 函数也称原子轨道。但这里所说的原子轨道和宏观物体固定轨道的含义不同,它只是反 映了核外电子运动状态表现出的波动性和统计性规律。 为了方便,解方程时一般先将空间坐标 (x,y,z)转换成球坐标 (r,, ),而后把() 分解为用 r 表示的径向分布函数 R(r)和仅包含角度变量和的角度分布函数 Y()。R 为电 子与原子核间的距离,和代表角度。由于的角度分布与主量子数 l 无关,且 l 相同时, 其角度分布图总是一样的。在下章讨论成键问题时,角度分布图有直接应用,故比较重 要。图 3-1 为某些原子轨道的角度分布图,图中的“+”、“-”号表示波函数的正、负值
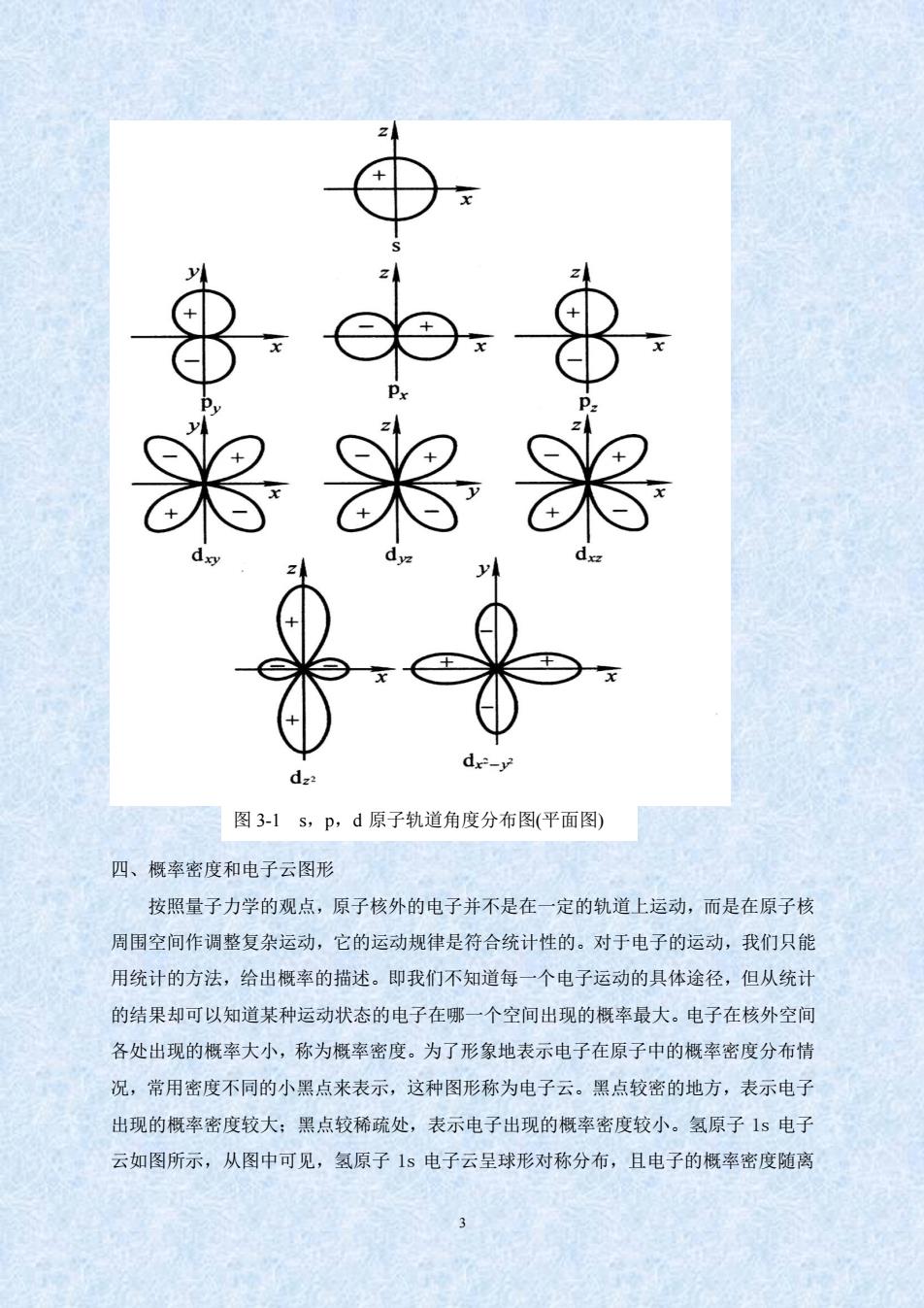
8 岛 图3-1s,P,d原子轨道角度分布图(平面图) 四、概率密度和电子云图形 按照量子力学的观点,原子核外的电子并不是在一定的轨道上运动,而是在原子核 周围空间作调整复杂运动,它的运动规律是符合统计性的。对于电子的运动,我们只能 用统计的方法,给出概率的描述。即我们不知道每一个电子运动的具体途径,但从统计 的结果却可以知道某种运动状态的电子在哪一个空间出现的概率最大。电子在核外空间 各处出现的概率大小,称为概率密度。为了形象地表示电子在原子中的概率密度分布情 况,常用密度不同的小黑点来表示,这种图形称为电子云。黑点较密的地方,表示电子 出现的概率密度较大:黑点较稀疏处,表示电子出现的概率密度较小。氢原子1s电子 云如图所示,从图中可见,氢原子15电子云呈球形对称分布,且电子的概率密度随离
3 四、概率密度和电子云图形 按照量子力学的观点,原子核外的电子并不是在一定的轨道上运动,而是在原子核 周围空间作调整复杂运动,它的运动规律是符合统计性的。对于电子的运动,我们只能 用统计的方法,给出概率的描述。即我们不知道每一个电子运动的具体途径,但从统计 的结果却可以知道某种运动状态的电子在哪一个空间出现的概率最大。电子在核外空间 各处出现的概率大小,称为概率密度。为了形象地表示电子在原子中的概率密度分布情 况,常用密度不同的小黑点来表示,这种图形称为电子云。黑点较密的地方,表示电子 出现的概率密度较大;黑点较稀疏处,表示电子出现的概率密度较小。氢原子 1s 电子 云如图所示,从图中可见,氢原子 1s 电子云呈球形对称分布,且电子的概率密度随离 图 3-1 s,p,d 原子轨道角度分布图(平面图)
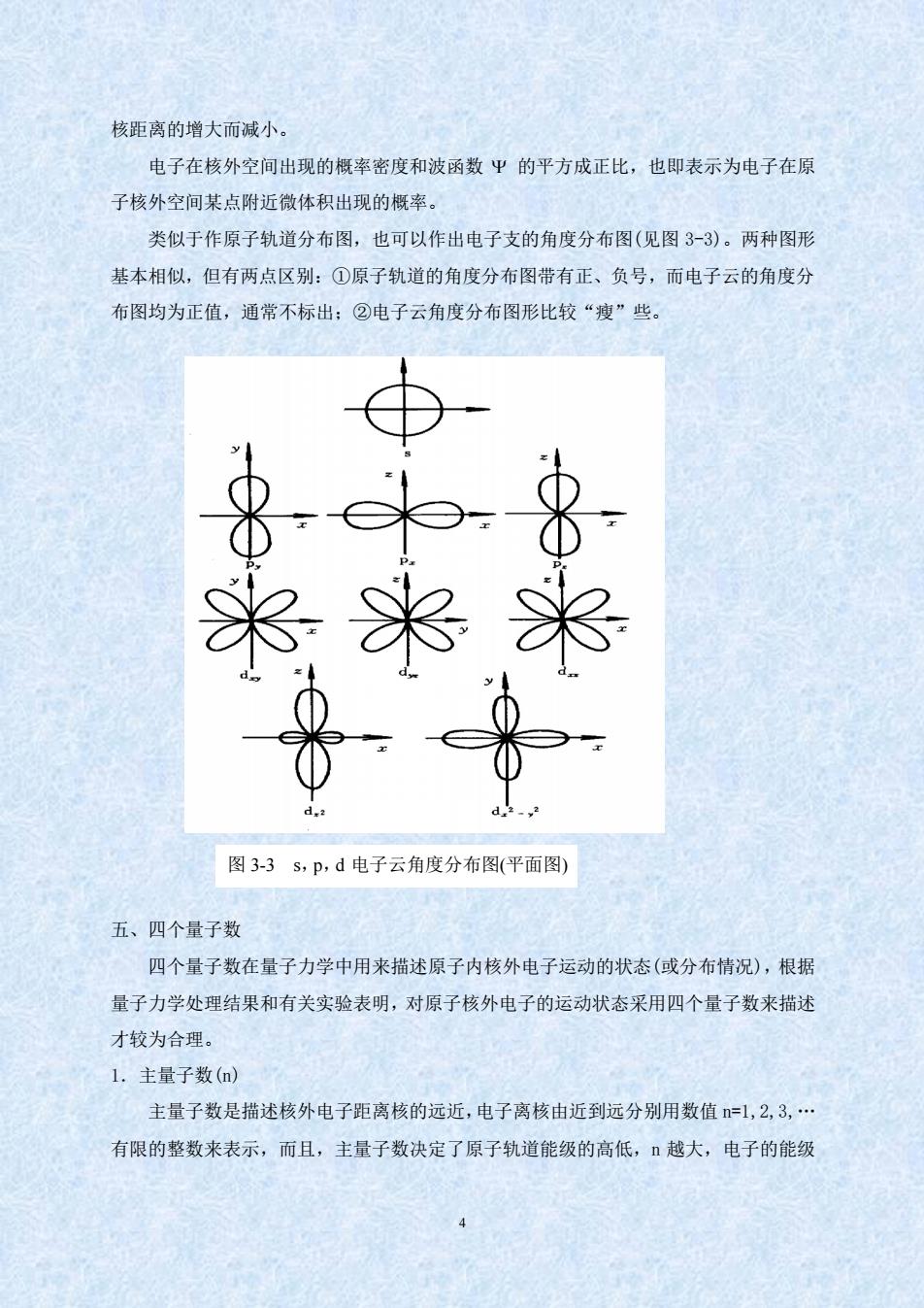
核距离的增大而减小。 电子在核外空间出现的概率密度和波函数平的平方成正比,也即表示为电子在原 子核外空间某点附近微体积出现的概率。 类似于作原子轨道分布图,也可以作出电子支的角度分布图(见图3-3)。两种图形 基本相似,但有两点区别:①原子轨道的角度分布图带有正、负号,而电子云的角度分 布图均为正值,通常不标出:②电子云角度分布图形比较“瘦”些。 米 米 米 图3-3s,p,d电子云角度分布图(平面图) 五、四个量子数 四个量子数在量子力学中用来描述原子内核外电子运动的状态(或分布情况),根据 量子力学处理结果和有关实验表明,对原子核外电子的运动状态采用四个量子数来描述 才较为合理。 L.主量子数() 主量子数是描述核外电子距离核的远近,电子离核由近到远分别用数值=1,2,3,· 有限的整数来表示,而且,主量子数决定了原子轨道能级的高低,越大,电子的能级
4 核距离的增大而减小。 电子在核外空间出现的概率密度和波函数 的平方成正比,也即表示为电子在原 子核外空间某点附近微体积出现的概率。 类似于作原子轨道分布图,也可以作出电子支的角度分布图(见图 3-3)。两种图形 基本相似,但有两点区别:①原子轨道的角度分布图带有正、负号,而电子云的角度分 布图均为正值,通常不标出;②电子云角度分布图形比较“瘦”些。 五、四个量子数 四个量子数在量子力学中用来描述原子内核外电子运动的状态(或分布情况),根据 量子力学处理结果和有关实验表明,对原子核外电子的运动状态采用四个量子数来描述 才较为合理。 1.主量子数(n) 主量子数是描述核外电子距离核的远近,电子离核由近到远分别用数值 n=1,2,3,. 有限的整数来表示,而且,主量子数决定了原子轨道能级的高低,n 越大,电子的能级 图 3-3 s,p,d 电子云角度分布图(平面图)
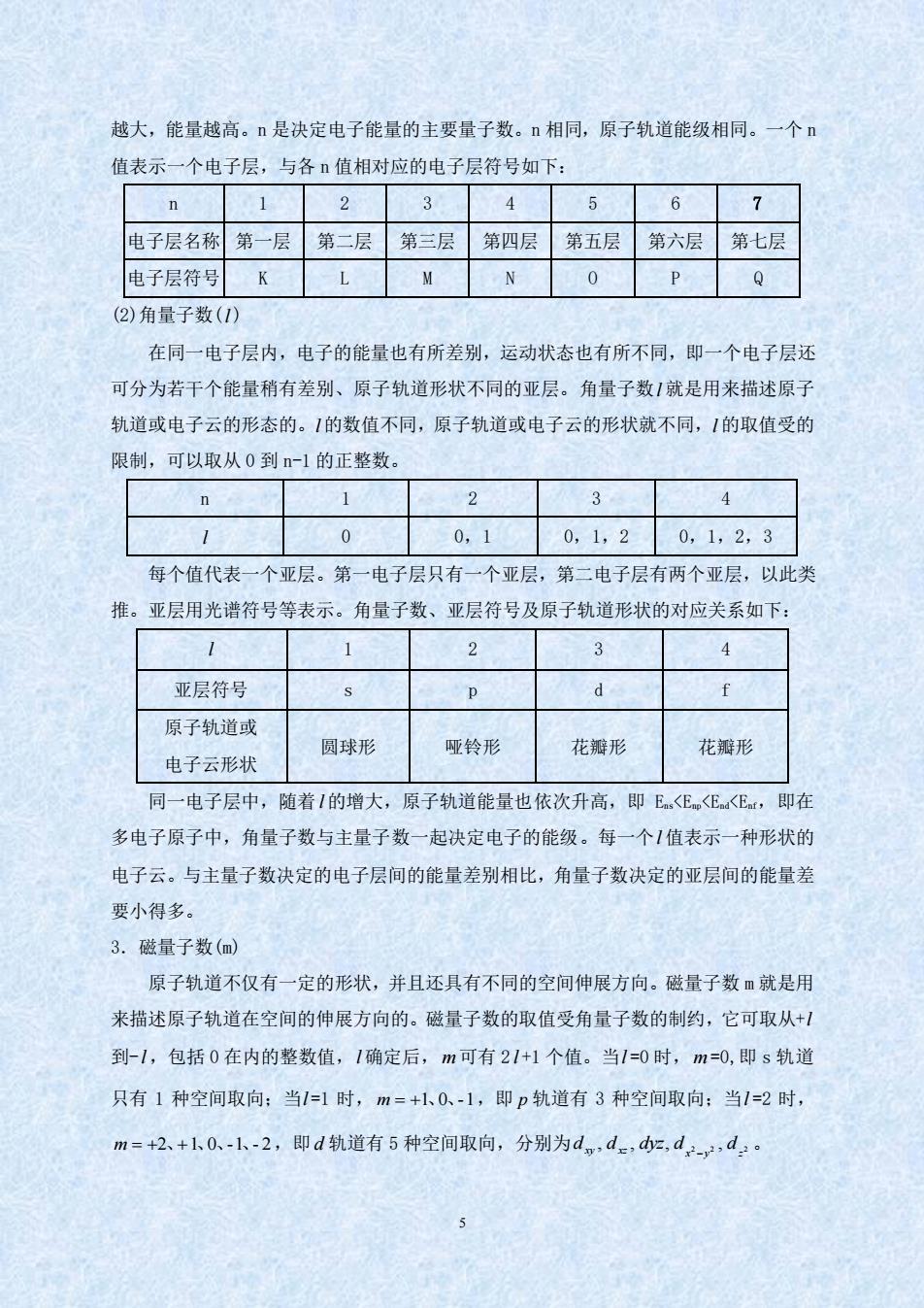
越大,能量越高。n是决定电子能量的主要量子数。n相同,原子轨道能级相同。一个 值表示一个电子层,与各n值相对应的电子层符号如下: n 1234 5 6 7 电子层名称第一层第二层第三层第四层第五层第六层第七层 电子层符号KLMN 0 Q 2)角量子数(1) 在同一电子层内,电子的能量也有所差别,运动状态也有所不同,即一个电子层还 可分为若干个能量稍有差别、原子轨道形状不同的亚层。角量子数1就是用来描述原子 轨道或电子云的形态的。1的数值不同,原子轨道或电子云的形状就不同,1的取值受的 限制,可以取从0到n-1的正整数 n 2 3 4 1 0 0,10,1,20,1,2,3 每个值代表一个亚层。第一电子层只有一个亚层,第二电子层有两个亚层,以此类 推。亚层用光谱符号等表示。角量子数、亚层符号及原子轨道形状的对应关系如下: 1 1 2 3 4 亚层符号 原子轨道或 电子云形状 园球形 哑铃形 花瓣形 花瓣形 同一电子层中,随着1的增大,原子轨道能量也依次升高,即E<E<E。,即在 多电子原子中,角量子数与主量子数一起决定电子的能级。每一个1值表示一种形状的 电子云。与主量子数决定的电子层间的能量差别相比,角量子数决定的亚层间的能量差 要小得多。 3.磁量子数(m) 原子轨道不仅有一定的形状,并且还具有不同的空间伸展方向。磁量子数m就是用 来描述原子轨道在空间的伸展方向的。磁量子数的取值受角量子数的制约,它可取从+ 到-1,包括0在内的整数值,1确定后,m可有21+1个值。当1=0时,m=0,即s轨道 只有1种空间取向:当1=1时,m=+1、0、-1,即p轨道有3种空间取向:当1=2时, m=+2、+1k0-1、-2,即d轨道有5种空间取向,分别为d,d.,d,d:
5 越大,能量越高。n 是决定电子能量的主要量子数。n 相同,原子轨道能级相同。一个 n 值表示一个电子层,与各 n 值相对应的电子层符号如下: n 1 2 3 4 5 6 7 电子层名称 第一层 第二层 第三层 第四层 第五层 第六层 第七层 电子层符号 K L M N O P Q (2)角量子数( l ) 在同一电子层内,电子的能量也有所差别,运动状态也有所不同,即一个电子层还 可分为若干个能量稍有差别、原子轨道形状不同的亚层。角量子数 l 就是用来描述原子 轨道或电子云的形态的。 l 的数值不同,原子轨道或电子云的形状就不同, l 的取值受的 限制,可以取从 0 到 n-1 的正整数。 n 1 2 3 4 l 0 0,1 0,1,2 0,1,2,3 每个值代表一个亚层。第一电子层只有一个亚层,第二电子层有两个亚层,以此类 推。亚层用光谱符号等表示。角量子数、亚层符号及原子轨道形状的对应关系如下: l 1 2 3 4 亚层符号 s p d f 原子轨道或 电子云形状 圆球形 哑铃形 花瓣形 花瓣形 同一电子层中,随着 l 的增大,原子轨道能量也依次升高,即 Ens<Enp<End<Enf,即在 多电子原子中,角量子数与主量子数一起决定电子的能级。每一个 l 值表示一种形状的 电子云。与主量子数决定的电子层间的能量差别相比,角量子数决定的亚层间的能量差 要小得多。 3.磁量子数(m) 原子轨道不仅有一定的形状,并且还具有不同的空间伸展方向。磁量子数 m 就是用 来描述原子轨道在空间的伸展方向的。磁量子数的取值受角量子数的制约,它可取从+ l 到- l ,包括 0 在内的整数值, l 确定后, m 可有 2 l +1 个值。当 l =0 时, m =0,即 s 轨道 只有 1 种空间取向;当 l =1 时, m = +1、0、-1 ,即 p 轨道有 3 种空间取向;当 l =2 时, m = +2、+1、0、-1、- 2 ,即 d 轨道有 5 种空间取向,分别为 , , , 2 2 , 2 x y z dxy dxz dyz d d −
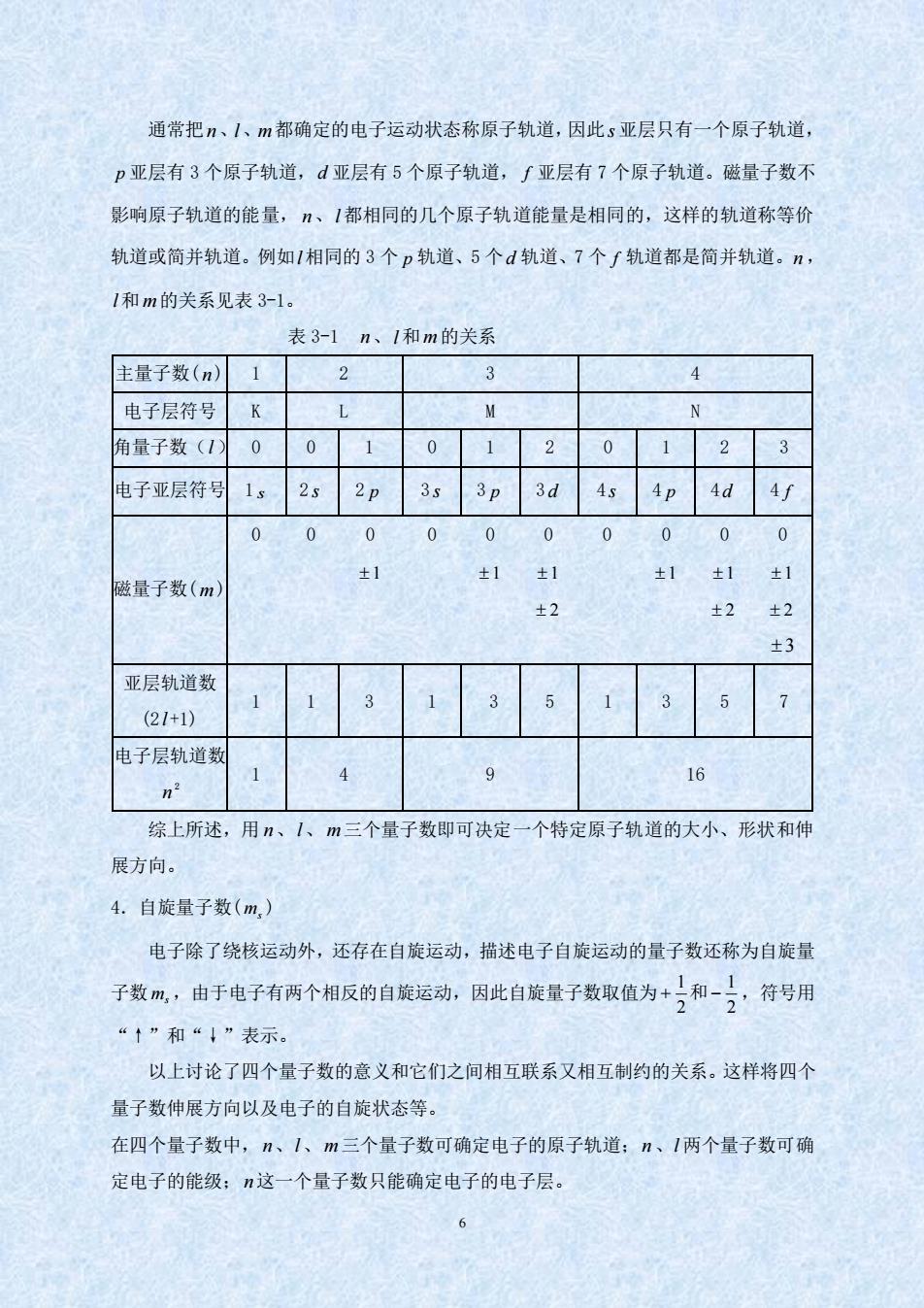
通常把、1、m都确定的电子运动状态称原子轨道,因此s亚层只有一个原子轨道, p亚层有3个原子轨道,d亚层有5个原子轨道,∫亚层有7个原子轨道。磁量子数不 影响原子轨道的能量,、1都相同的几个原子轨道能量是相同的,这样的轨道称等价 轨道或简并轨道。例如1相同的3个p轨道、5个d轨道、7个∫轨道都是简并轨道。n, 1和m的关系见表3-1。 表3-1n、1和m的关系 主量子数(n)1 2 3 4 电子层符号K N 角量子数(10 0 0 120123 电子亚层符号1s2s2p 3s 3p 3d 4s 4p 4d 4f 0 0 0 000000 0 ±1 ±1±1 ±1 ±1 磁量子数(m) ±1 ±2 ±2 ±2 +3 亚层轨道数 35 3 (21+1) 电子层轨道数 n2 9 16 综上所述,用n、1、m三个量子数即可决定一个特定原子轨道的大小、形状和伸 展方向。 4.自旋量子数(m,) 电子除了绕核运动外,还存在自旋运动,描述电子自旋运动的量子数还称为自旋量 子数m,由于电子有两个相反的自旋运动,因此自旋量子数取值为+)和-),符号用 “↑”和“↓”表示。 以上讨论了四个量子数的意义和它们之间相互联系又相互制约的关系。这样将四个 量子数伸展方向以及电子的自旋状态等。 在四个量子数中,n、1、m三个量子数可确定电子的原子轨道:n、1两个量子数可确 定电子的能级:n这一个量子数只能确定电子的电子层。 6
6 通常把 n、l、m 都确定的电子运动状态称原子轨道,因此 s 亚层只有一个原子轨道, p 亚层有 3 个原子轨道, d 亚层有 5 个原子轨道, f 亚层有 7 个原子轨道。磁量子数不 影响原子轨道的能量, n、l 都相同的几个原子轨道能量是相同的,这样的轨道称等价 轨道或简并轨道。例如 l 相同的 3 个 p 轨道、5 个 d 轨道、7 个 f 轨道都是简并轨道。 n , l 和 m 的关系见表 3-1。 表 3-1 n、l 和 m 的关系 主量子数( n ) 1 2 3 4 电子层符号 K L M N 角量子数( l ) 0 0 1 0 1 2 0 1 2 3 电子亚层符号 1 s 2 s 2 p 3 s 3 p 3 d 4 s 4 p 4 d 4 f 磁量子数( m ) 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 2 2 2 3 亚层轨道数 (2 l +1) 1 1 3 1 3 5 1 3 5 7 电子层轨道数 n 2 1 4 9 16 综上所述,用 n、l 、m 三个量子数即可决定一个特定原子轨道的大小、形状和伸 展方向。 4.自旋量子数( ms ) 电子除了绕核运动外,还存在自旋运动,描述电子自旋运动的量子数还称为自旋量 子数 ms ,由于电子有两个相反的自旋运动,因此自旋量子数取值为 2 1 2 1 + 和 − ,符号用 “↑”和“↓”表示。 以上讨论了四个量子数的意义和它们之间相互联系又相互制约的关系。这样将四个 量子数伸展方向以及电子的自旋状态等。 在四个量子数中, n、l 、m 三个量子数可确定电子的原子轨道; n、l 两个量子数可确 定电子的能级; n 这一个量子数只能确定电子的电子层
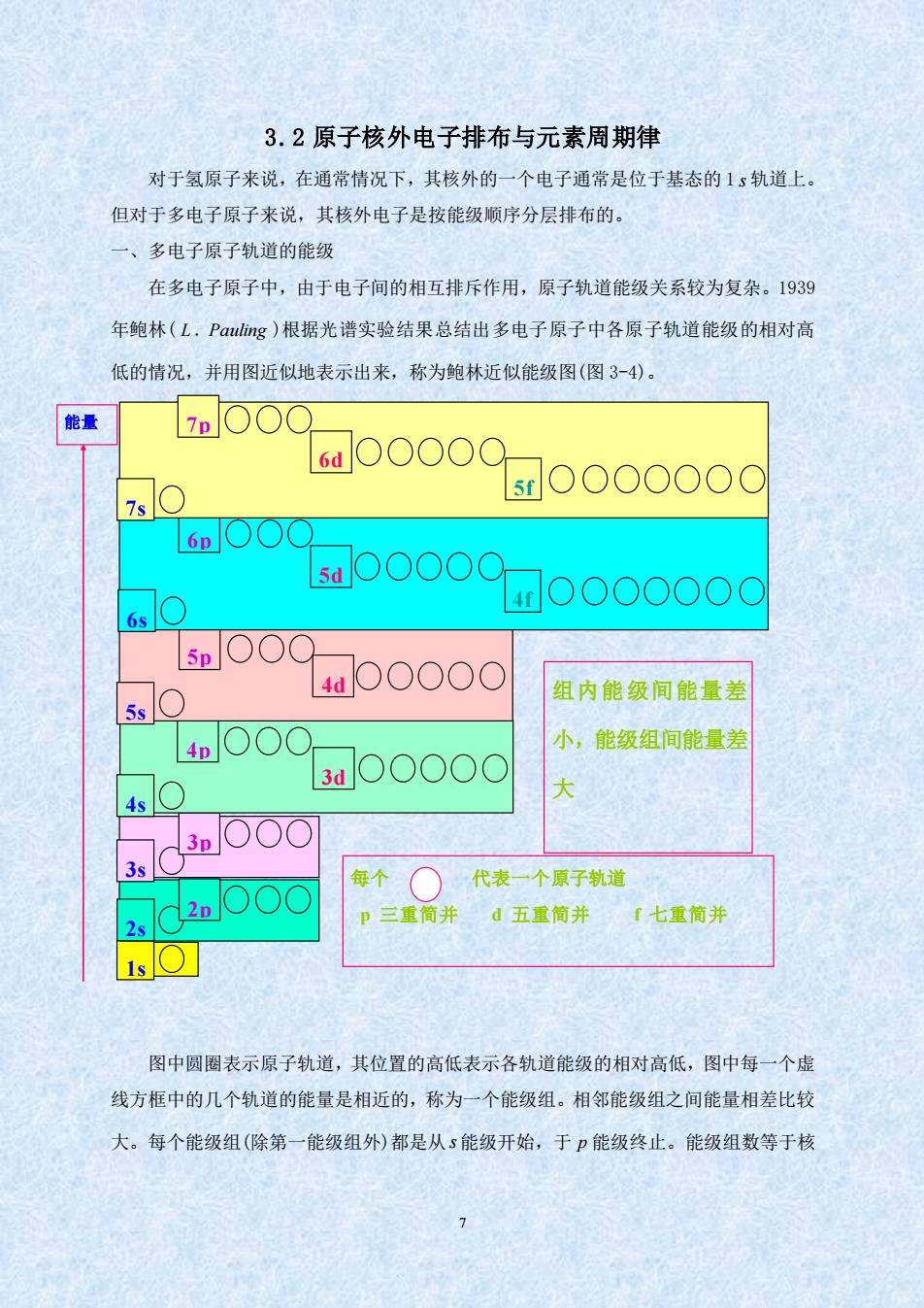
3.2原子核外电子排布与元素周期律 对于氢原子来说,在通常情况下,其核外的一个电子通常是位于基态的1s轨道上。 但对于多电子原子来说,其核外电子是按能级顺序分层排布的。 多电子原子轨道的能级 在多电子原子中,由于电子间的相互排斥作用,原子轨道能级关系较为复杂。1939 年鲍林(L.Pag)根据光谱实验结果总结出多电子原子中各原子轨道能级的相对高 低的情况,并用图近似地表示出来,称为鲍林近似能级图(图3-4), 能量 1000 6dO000 si0O00000 60 sd 000 a0000000 5000 4d000 组内能级间能量差 4nO00 小,能级组间能量差 3a00000 4s1○ 大 300 3s 每个○代表一个原子轨道 p三重简并d五重简并r七重简并 2s 1sO 图中圆圈表示原子轨道,其位置的高低表示各轨道能级的相对高低,图中每一个虚 线方框中的几个轨道的能量是相近的,称为一个能级组。相邻能级组之间能量相差比较 大。每个能级组(除第一能级组外)都是从s能级开始,于能级终止。能级组数等于核
7 3.2 原子核外电子排布与元素周期律 对于氢原子来说,在通常情况下,其核外的一个电子通常是位于基态的 1 s 轨道上。 但对于多电子原子来说,其核外电子是按能级顺序分层排布的。 一、多电子原子轨道的能级 在多电子原子中,由于电子间的相互排斥作用,原子轨道能级关系较为复杂。1939 年鲍林( L . Pauling )根据光谱实验结果总结出多电子原子中各原子轨道能级的相对高 低的情况,并用图近似地表示出来,称为鲍林近似能级图(图 3-4)。 图中圆圈表示原子轨道,其位置的高低表示各轨道能级的相对高低,图中每一个虚 线方框中的几个轨道的能量是相近的,称为一个能级组。相邻能级组之间能量相差比较 大。每个能级组(除第一能级组外)都是从 s 能级开始,于 p 能级终止。能级组数等于核 能量 1s 2s 2p 3s 3p 4s 4p 3d 5s 5p 4d 6s 6p 5d 4f 组内能级间能量差 小,能级组间能量差 大 每个 代表一个原子轨道 p 三重简并 d 五重简并 f 七重简并 7s 7p 6d 5f

外电子层数。能级组的划分与周期表中周期的划分是一致的。从图3-4可以看出 (①)同一原子中的同一电子层内,各亚层之间的能量次序为s<p<d<时 (②)同一原子中的不同电子层内,相同类型亚层之间的能量次序为 1s<2s<3s<;2p<3P<4p. (③)同一原子中第三层以上的电子层中,不同类型的亚层之间,在能级组中常出现能 级交错现象,如: 4s<3d<4p,5s<4d<5p6s<4∫<5d<6p 对于鲍林近似能级图,需要注意以下几点: (1)它只有近似的意义,不可能完全反映出每个原子轨道能级的相对高低。 (②)它只能反映同一原子内各原子轨道能级的相对高低,不能用鲍林近似能级图来 比较不同元素原子轨道能级的相对高低。 (3)该图实际上只能反映出同一原子外电子层中原子轨道能级的相对高低,而不一 定能完全反映内电子层中原子轨道能级的相对高低。 (④)电子在某一轨道上的能量,实际上与原子序数(核电荷数)有关。核电荷数越大 对电子的吸引力越大,电子离核越近,轨道能量就降得越低。轨道能级之间的相对高低 情况,与鲍林近似能级图会有所不同, 二、基态原子中电子的排布 1.基态原子中电子的排布原理 根据光谱实验结果和量子力学理论,核外电子排布服从以下原则: (①)能量最低原理自然界中任何体系总是能量越低,所处的状态越稳定,这个规 律称为能量最低原理。原子核外电子的排布也遵循这个原理。所以,随着原子序数的递 增,电子总是优先进入能量最低的能级,可依鲍林近似能级图逐级填入
8 外电子层数。能级组的划分与周期表中周期的划分是一致的。从图 3-4 可以看出: (1)同一原子中的同一电子层内,各亚层之间的能量次序为 ns np nd nf 。 (2)同一原子中的不同电子层内,相同类型亚层之间的能量次序为 1s 2s 3s ; 2 p 3P 4 p (3)同一原子中第三层以上的电子层中,不同类型的亚层之间,在能级组中常出现能 级交错现象,如: 4s 3d 4 p; 5s 4d 5p; 6s 4 f 5d 6 p 对于鲍林近似能级图,需要注意以下几点: (1)它只有近似的意义,不可能完全反映出每个原子轨道能级的相对高低。 (2)它只能反映同一原子内各原子轨道能级的相对高低,不能用鲍林近似能级图来 比较不同元素原子轨道能级的相对高低。 (3)该图实际上只能反映出同一原子外电子层中原子轨道能级的相对高低,而不一 定能完全反映内电子层中原子轨道能级的相对高低。 (4)电子在某一轨道上的能量,实际上与原子序数(核电荷数)有关。核电荷数越大, 对电子的吸引力越大,电子离核越近,轨道能量就降得越低。轨道能级之间的相对高低 情况,与鲍林近似能级图会有所不同。 二、基态原子中电子的排布 1.基态原子中电子的排布原理 根据光谱实验结果和量子力学理论,核外电子排布服从以下原则: (1)能量最低原理 自然界中任何体系总是能量越低,所处的状态越稳定,这个规 律称为能量最低原理。原子核外电子的排布也遵循这个原理。所以,随着原子序数的递 增,电子总是优先进入能量最低的能级,可依鲍林近似能级图逐级填入

@ a ⑦ @ @ 面 图 ⑧ 仰 4@ © @ 3@ ② p © 基态原子外层电子填充顺序为→(n-2)f→(n-1)d→p(如图3-5)。但要注意 的是基态原子失去外层电子的顺序为p→s→(n-→(n-2,和填充时的并不对 (2)泡利不相容原理1929年,奥地利科学家泡利(W.Pah)提出:在同一原子中 不可能有四个量子数完全相同的2个电子,即每个轨道最多只能容纳2个自旋方向相反 的电子。应用泡利不相容原理,可以推算出每一电子层上电子的最大容量为2。参见 表3-1。 (3)洪德规则德国科学家洪德(F.hmd)根据大量光谱实验数据提出:在同一亚 层的等价轨道上,电子将尽可能占据不同的轨道,且自旋方向相同。此外洪德根据光谱 实验,又总结出另一条规则:等价轨道在全充满、半充满或全空的状态下是比较稳定的。 即: p或d或rH 全充满 p或d或r 半充满 p或d或f° 全空 2.基态原子中电子的排布
9 基态原子外层电子填充顺序为 ns → (n − 2) f → (n −1)d → np (如图 3-5)。但要注意 的是基态原子失去外层电子的顺序为 np → ns → (n −1)d → (n − 2) f ,和填充时的并不对 应。 (2)泡利不相容原理 1929 年,奥地利科学家泡利( W . Pauli )提出:在同一原子中 不可能有四个量子数完全相同的 2 个电子,即每个轨道最多只能容纳 2 个自旋方向相反 的电子。应用泡利不相容原理,可以推算出每一电子层上电子的最大容量为 2 n 2。参见 表 3-1。 (3)洪德规则 德国科学家洪德( F . Hund )根据大量光谱实验数据提出:在同一亚 层的等价轨道上,电子将尽可能占据不同的轨道,且自旋方向相同。此外洪德根据光谱 实验,又总结出另一条规则:等价轨道在全充满、半充满或全空的状态下是比较稳定的。 即: 或 或 全 空 或 或 半充满 或 或 全充满 0 0 0 3 5 7 6 10 14 p d f p d f p d f 2.基态原子中电子的排布

根据上述三条原理、规则,就可以确定大多数元素的基态原子中电子的排布情况。 电子在核外的排布常称为电子层构型(简称电子构型)通常有三种表示方法: (1)电子排布式按电子在原子核外各亚层中分布的情况,在亚层符号的右上角注 明排列的电子数。例如::4A,其电子排布式为1s22s22p3s23p:又如:B,其电 子排布式为1s22s22p3s23p3d4s24p。 由于参加化学反应的只是原子的外层电子,内层电子结构一般是不变的,因此,可 以用“原子实”来表示原子的内层电子结构。当内层电子构型与稀有气体的电子构型相 同时,就用该稀有气体的元素符号来表示原子的内层电子构型,并称之为原子实。如以 上两例的电子排布也可简写成: 1 Al [Ne]s23p'3s Br [Ar]d04s24ps 又例如铬和铜原子核外电子的排布式,根据洪德规则的特例: 2Cr不是1s22s22p3s23p3d4s2,而是1s22s22p3s23p3d°4s。3d54s都为半充 满。 2C4不是1s22s22p3s23p3d°4s2,而是1s22s22p323p53d04s。3d0为全充满,45 为半充满。 (②)轨道表示式按电子在核外原子轨道中的分布情况,用一个圆圈或一个方格表 示一个原子轨道(简并轨道的圆圈或方格连在一起),用向上或向下箭头表示电子的自旋 状态。例如: nNa (③)用量子数表示即按所处的状态用整套量子数表示。原子核外电子的运动状态 是由四个量子数确定的,为此可表示如下: 6PNaB3p),则3这2个电子用整套量子数表示为8,0,0,+:30,0,- 3p这3个电子用整套量子数表示为3,1,-1,+:3,1,0,+31.1,+ 表3-2列出了由光谱实验数据得到的原子序数1~109各元素基态原子中的电子排布 情况。其中绝大多数元素的电子排布与上节所述的排布原则是一致的,但也有少数不符 合。对此,必须尊重事实,并在此基础上去探求更符合实际的理论解释
10 根据上述三条原理、规则,就可以确定大多数元素的基态原子中电子的排布情况。 电子在核外的排布常称为电子层构型(简称电子构型)通常有三种表示方法: (1)电子排布式 按电子在原子核外各亚层中分布的情况,在亚层符号的右上角注 明排列的电子数。例如: Al 13 ,其电子排布式为 2 2 6 2 1 1s 2s 2p 3s 3p ;又如: Br 35 ,其电 子排布式为 2 2 6 2 6 10 2 5 1s 2s 2p 3s 3p 3d 4s 4p 。 由于参加化学反应的只是原子的外层电子,内层电子结构一般是不变的,因此,可 以用“原子实”来表示原子的内层电子结构。当内层电子构型与稀有气体的电子构型相 同时,就用该稀有气体的元素符号来表示原子的内层电子构型,并称之为原子实。如以 上两例的电子排布也可简写成: Al 13 2 1 [Ne]3s 3p Br 35 10 2 5 [Ar]3d 4s 4p 又例如铬和铜原子核外电子的排布式,根据洪德规则的特例: 24Cr 不是1s 2 2s 2 2p 6 3s 2 3p 6 3d 4 4s 2 , 而是 2 2 6 2 6 5 1 1s 2s 2p 3s 3p 3d 4s 。 5 1 3d 4s 都为半充 满。 2 2 6 2 6 9 2 29Cu 不是1s 2s 2 p 3s 3p 3d 4s ,而是 2 2 6 2 6 10 1 1s 2s 2p 3s 3p 3d 4s 。 10 3d 为全充满, 1 4s 为半充满。 (2)轨道表示式 按电子在核外原子轨道中的分布情况,用一个圆圈或一个方格表 示一个原子轨道(简并轨道的圆圈或方格连在一起),用向上或向下箭头表示电子的自旋 状态。例如: 11Na ○↑ (3)用量子数表示 即按所处的状态用整套量子数表示。原子核外电子的运动状态 是由四个量子数确定的,为此可表示如下: ([ ]3 3 ) 2 3 15 P Ne s p ,则 2 3s 这 2 个电子用整套量子数表示为 3,0,0, 2 1 + ; 2 1 3, 0, 0, − ; 3 3p 这 3 个电子用整套量子数表示为 3,1,-1, 2 1 + ;3,1,0, 2 1 + ;3,1,1, 2 1 + 。 表 3-2 列出了由光谱实验数据得到的原子序数 1~109 各元素基态原子中的电子排布 情况。其中绝大多数元素的电子排布与上节所述的排布原则是一致的,但也有少数不符 合。对此,必须尊重事实,并在此基础上去探求更符合实际的理论解释