电子科技大学：《机器学习 Machine Learning》课程教学资源（课件讲稿）第4章 回归分类

回归分类 电子科技大学 师君

电子科技大学 师 君

最小二乘问题 线性分类 广义线性分类 稀疏重建

最小二乘问题 线性分类 广义线性分类 稀疏重建

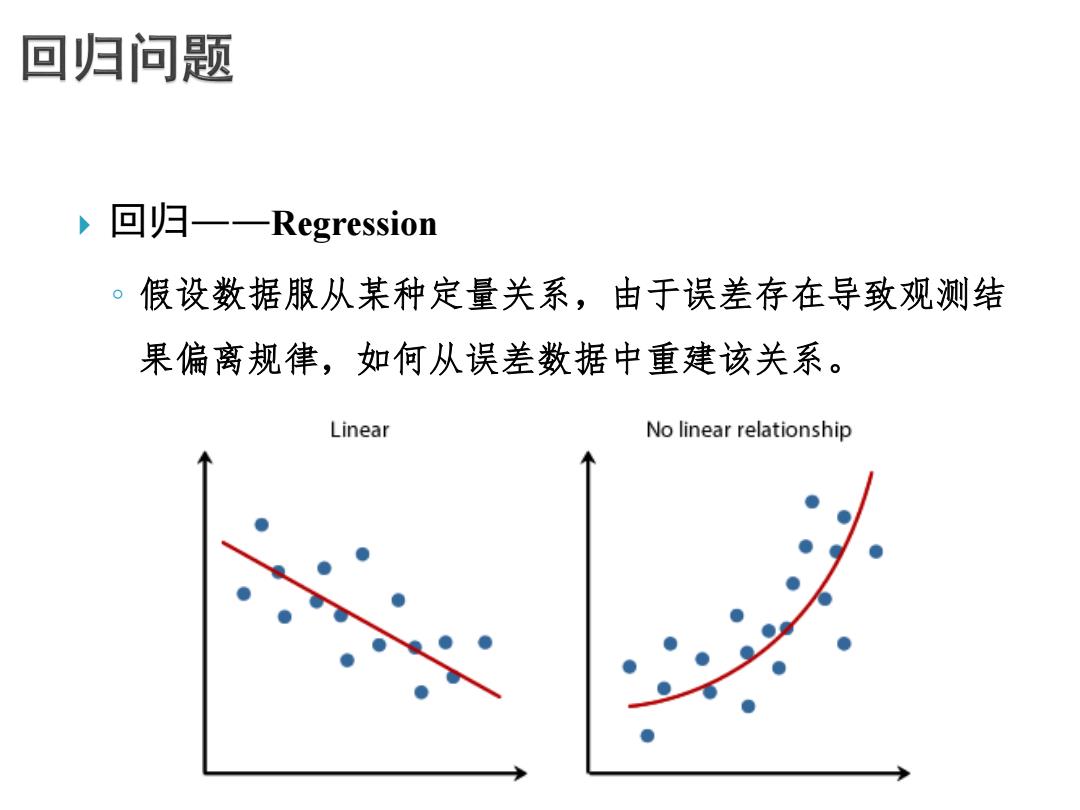
回归问题 ,回归一一Regression 。假设数据服从某种定量关系，由于误差存在导致观测结 果偏离规律，如何从误差数据中重建该关系。 Linear No linear relationship

 回归——Regression ◦ 假设数据服从某种定量关系，由于误差存在导致观测结 果偏离规律，如何从误差数据中重建该关系

回归问题 ,最小二乘准则 。回归残差 e;=f(x;w)-y e=leez,ex 。最小二乘准则： w*=argmin∑f(x;w）-y,'=argmin(e'c)

 最小二乘准则 ◦ 回归残差 ◦ 最小二乘准则：   2 * argmin ( ; ) argmin T i i i P f x w y      w w w e e  1 2  ( ; ) , ,... i i i T N e f y e e e    x w e

回归问题 ，线性回归 。狭义线性回归一一 线性函数 f(x;w)=wx 。广义线性回归一一基函数的线性组合 f(x;w)=>w:0:(x)=w"(o(x)) p(x)=((x)(x)..x(x)

 线性回归 ◦ 狭义线性回归——线性函数 ◦ 广义线性回归——基函数的线性组合 ( ; ) T f x w w x          1 2       ( ; ) ... T k k k T K f w        x w x w  φ x φ x x x x

回归问题 ,最小二乘问题的矩阵模型 。矩阵表示 e,=w'(p(x,))-y=(p(x,))w-x e=ΦW-y 9,(x1)p2().px() 0,(2）p2(2）…px(2) Φ 三 (xx)(xx)..(xx)

 最小二乘问题的矩阵模型 ◦ 矩阵表示                         1 1 2 1 1 1 2 2 2 2 1 2 ... ... ...... ... T T i i i i i K K N N K N e y y                         w φ x φ x w e w y x x x x x x x x x

回归问题 ,最小二乘问题的矩阵模型 w*arg min e=arg minw-y =argmin(e'e) =argmin[(Φw-y)'(Φw-y)]

 最小二乘问题的矩阵模型       2 2 2 2 * arg min arg min arg min arg min T T               w w w w w e w y e e w y w y

回归问题 ,最小二乘解 e'e=(④w-y)'(④w-y) =wIΦΦw-2wΦ'y+yy ae'e=2ΦΦw-2Φ'y=0 ∂w →w=(DΦ)'Φ'y MP广义逆矩阵

 最小二乘解       1 = 2 2 2 0 T T T T T T T T T T T T                        e e w y w y w w w y y y e e w y w w y MP广义逆矩阵

最小二乘问题 线性分类 广义线性分类 稀疏重建

最小二乘问题 线性分类 广义线性分类 稀疏重建

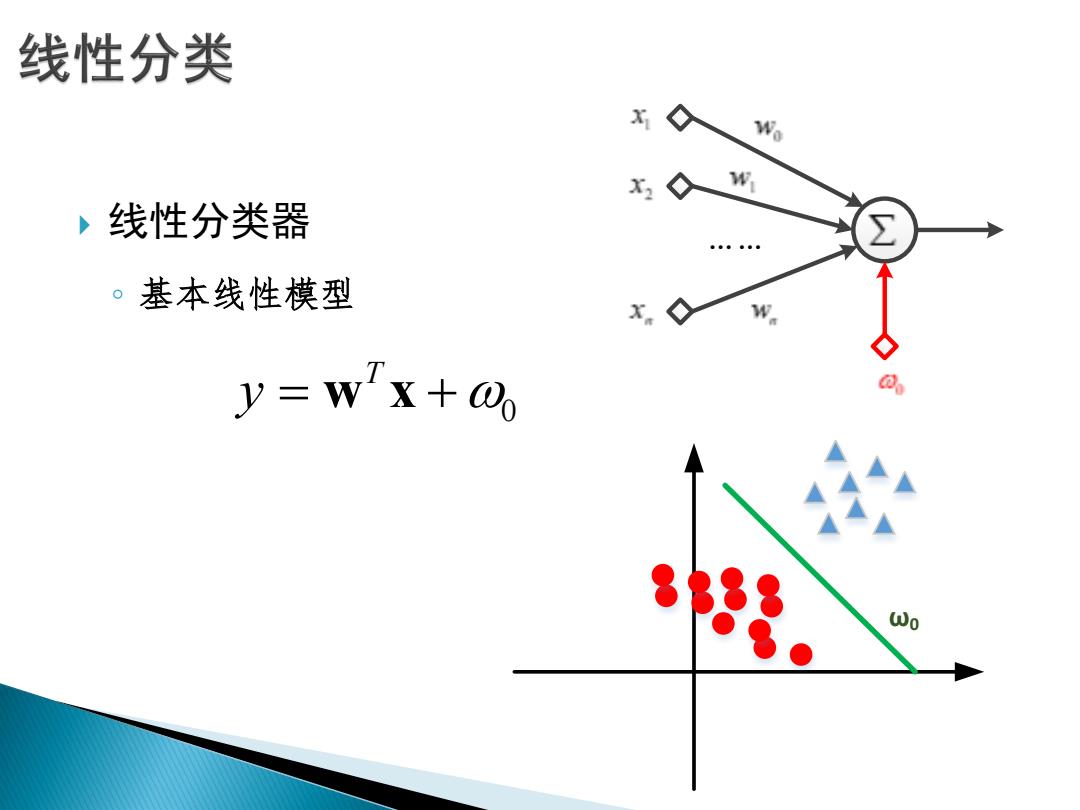
线性分类 W x2 w ，线性分类器 。基本线性模型 x y=Wx+0o 8。 Wo

 线性分类器 ◦ 基本线性模型 0 T y   w x  ω0