
支持向量机 电子科技大学 师君
电子科技大学 师 君

支特向量机 线性不可分问题 核T化支特向量机
支持向量机 线性不可分问题 核化支持向量机
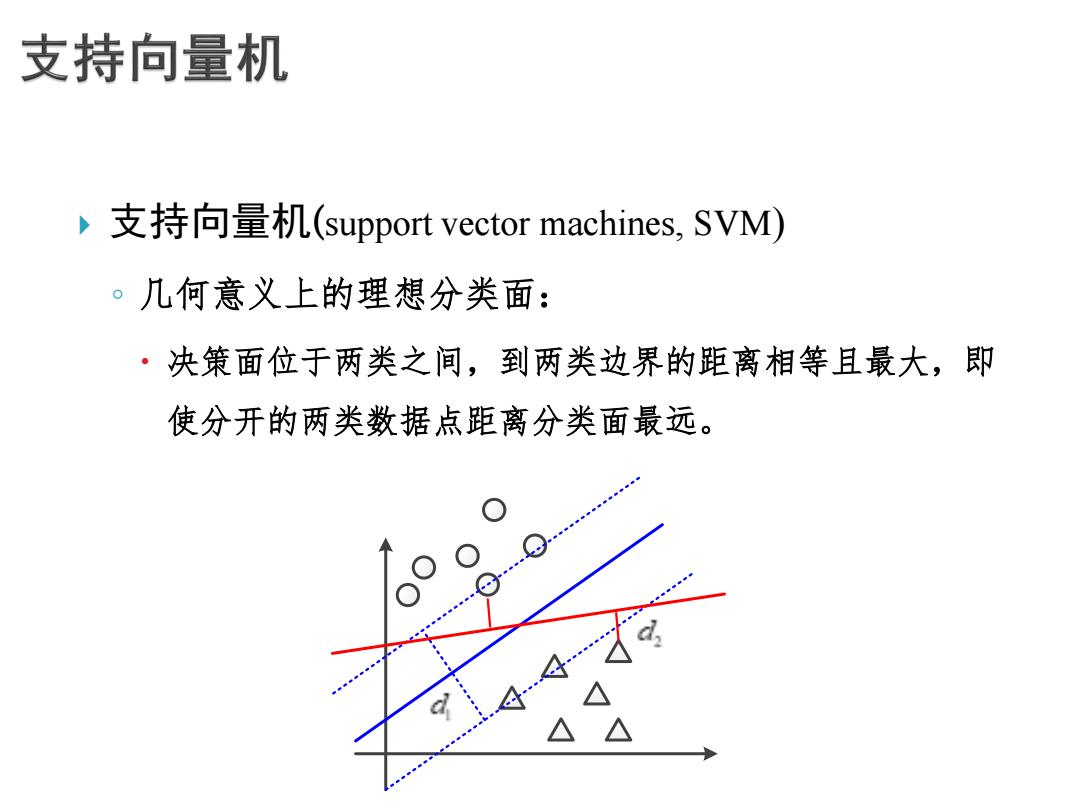
支持向量机 ,支持向量机(support vector machines,SVM) 。几何意义上的理想分类面: ·决策面位于两类之间,到两类边界的距离相等且最大,即 使分开的两类数据点距离分类面最远。 △△
支持向量机(support vector machines, SVM) ◦ 几何意义上的理想分类面: 决策面位于两类之间,到两类边界的距离相等且最大,即 使分开的两类数据点距离分类面最远

支持向量机 ,点到面的距离公式 平面方程:WX+w,=0 法线方程:X=Wt+Xo 交点为:=w% ww 距离为:d=Www=0
点到面的距离公式 0 0 0 0 0 0 0 - - = + = T T T T T w t w t w d t w x x w x w xw w w x w w w = 平面方程: 法线方程: 交点为: 距离为: =
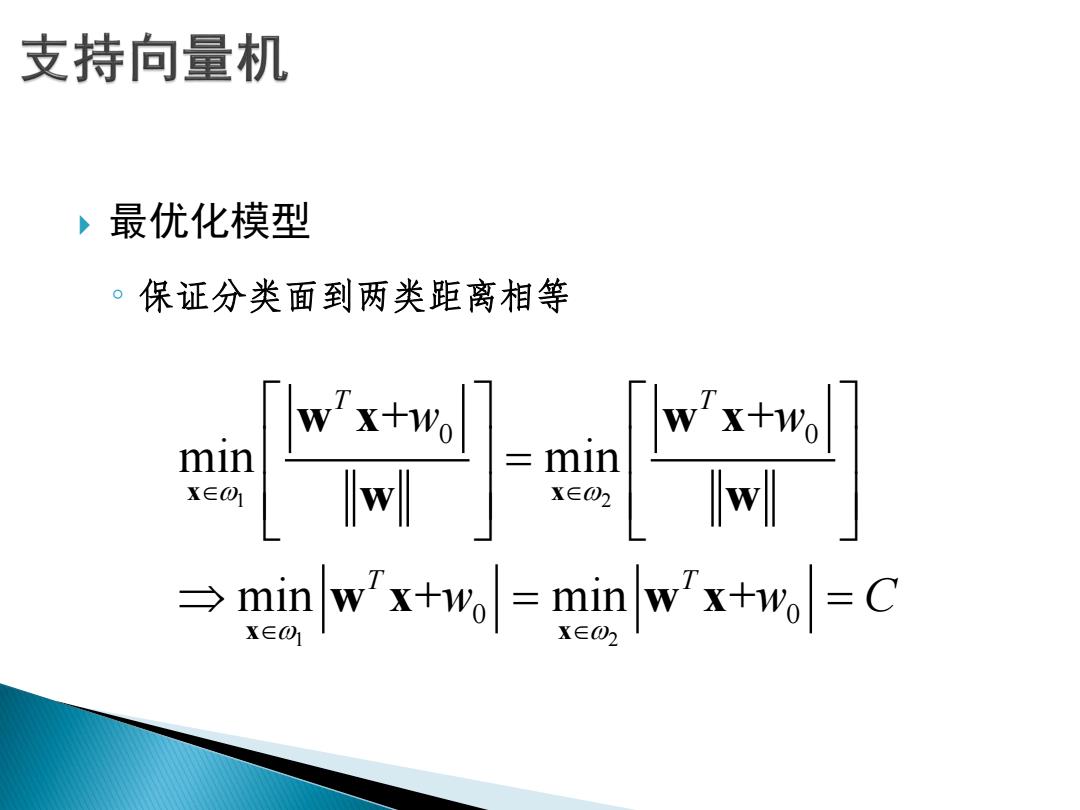
支持向量机 ,最优化模型 。保证分类面到两类距离相等 min w'x+wo K∈0 wT →minw'xh=minwx++e。=C
最优化模型 ◦ 保证分类面到两类距离相等 1 2 1 2 0 0 0 0 + + min min min + min + T T T T w w w w C x x x x w x w x w w w x w x

支持向量机 ,最优化模型 。保证分类面位于两类中间 wx+w≥C,X∈0 w'x+w≤-C,X∈02 。保证距离最大 ilei max
最优化模型 ◦ 保证分类面位于两类中间 ◦ 保证距离最大 0 1 0 2 + , + , T T w C w C w x x w x x max min C w w

支持向量机 ,最优化模型 。支持向量机最优化模型 minw st.:y,(wx,+wo)≥C=1,y,∈{-1,1} 。属于严格凸优化问题(二次最优化问题),解唯一
最优化模型 ◦ 支持向量机最优化模型 ◦ 属于严格凸优化问题(二次最优化问题),解唯一。 2 0 min . .: + 1, { 1,1} T i i i s t y w C y w w x

支持向量机 ,最优化求解一一KT转化 w,刘-wwy(xw)-可 (w,w2)=w-2[3,yx]=0→w=2[2yx】 Ow y,(wx+wo)≥1 见≥0 [y(wx,h)-1]=0
最优化求解——KKT转化 0 0 1 1 ( , , ) + 1 2 N T T i i i i L w y w w λ w w w x 0 1 1 0 0 ( , , ) 0 + 1 0 + 1 0 N N i i i i i i i i T i i i T i i i L w y y y w y w w λ w x w x w w xw x
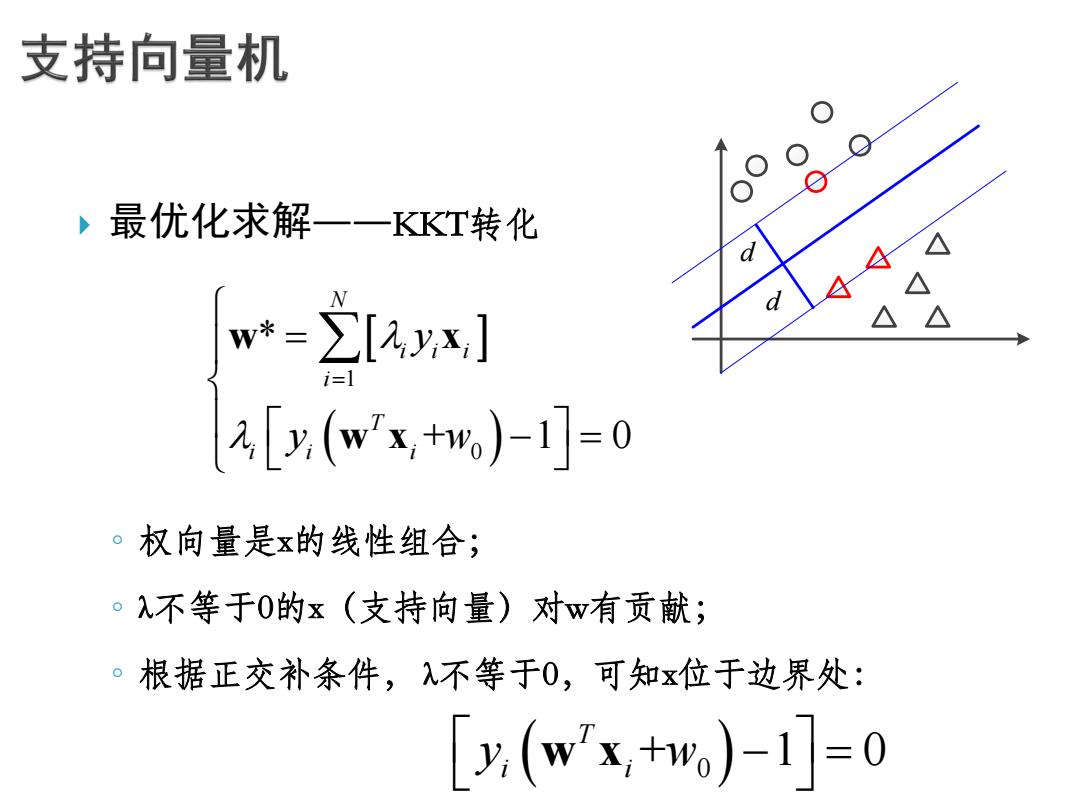
支持向量机 ,最优化求解一一KKT转化 公 △ w*=∑[,yx] 1 2[y(wx,+hw)-1]=0 。权向量是x的线性组合; 。不等于0的x(支持向量)对w有贡献; 。根据正交补条件,入不等于0,可知x位于边界处: [y(wx,+w)-1]=0
最优化求解——KKT转化 ◦ 权向量是x的线性组合; ◦ λ不等于0的x(支持向量)对w有贡献; ◦ 根据正交补条件, λ不等于0,可知x位于边界处: 1 0 * + 1 0 N i i i i T i i i y y w w x w x d d + 1 0 0 T i i y w w x

支持向量机 Z(w,w)=ww-立[(wXw,)-] ,最优化求解一一Wolfe对偶 max(L(w,wo)), 代价函数与特征空间x的维度没有 A.W,Wo 显式的关系。 w=∑[yx,] 先求解λ,后计算w ∑2y=0 1≥0 啤∑∑, ∑y,=0 入≥0
最优化求解——Wolfe对偶 0 0 , , 1 max ( , , ) , , 0 0 w N i i i i i i L w y y λ w w λ w x λ 1 1 max 2 0 0 N T i i j i j i j i i i y y y λ x x λ 0 0 1 1 ( , , ) + 1 2 N T T i i i i L w y w w λ w w w x 代价函数与特征空间x的维度没有 显式的关系。 先求解λ,后计算w