
最优T化回顾 电子科技大学 师君
电子科技大学 师 君

最优化问题 解的特点 问题转化 迭代法
最优化问题 解的特点 问题转化 迭代法

最优化问题 ,最优化一一寻找最大(小)值和对应位置: 。数值最优化一一连续(可导)问题的最值; ·最速下降、牛顿法、内点法… 。组合最优化一一离散问题的最值; ·最短路径、最优遍历… 。演化最优化一一通过随机搜索,寻找最值; ·模拟退火(SA)、遗传算法(GA)、微分进化(DE)、蚁群 算法(AA)、粒子群算法(PA)…
最优化——寻找最大(小)值和对应位置: ◦ 数值最优化——连续(可导)问题的最值; 最速下降、牛顿法、内点法…… ◦ 组合最优化——离散问题的最值; 最短路径、最优遍历…… ◦ 演化最优化——通过随机搜索,寻找最值; 模拟退火(SA)、遗传算法(GA)、微分进化(DE)、蚁群 算法(AA)、粒子群算法(PA)……

最优化问题概念 ,无约束最优化问题 minf(x),f(x):R”→R ,约束最优化问题: min f(x), f(x):R”→R Ceq,(x)=0 s.t.< Cie,(x)≥0
无约束最优化问题 约束最优化问题: min ( ), ( ) : n f f x x min ( ), ( ) : ( ) 0 . . ( ) 0 n i i f f Ceq s t Cie x x x x
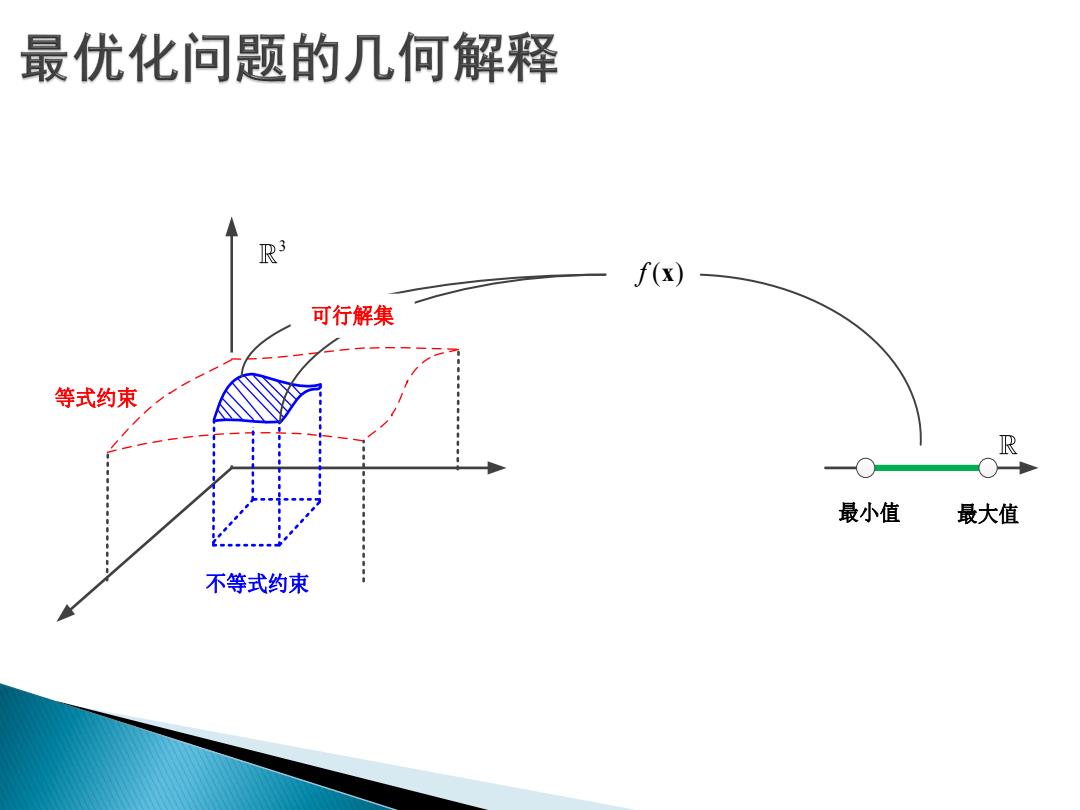
最优化问题的几何解释 R f(x) 可行解集 等式约束 R 最小值 最大值 不等式约束
( ) f x 不等式约束 等式约束 3 可行解集 最小值 最大值

最优解的存在性 ,最优化解存在的充分条件 。Weierstrass定理: (x)为连续函数 ①为紧密集 理解:1、实数域的紧密子集存在最大值和最小值 2、连续函数将紧密集映射为紧密集(利用柯西序列判 定)
最优化解存在的充分条件 ◦ Weierstrass定理: 理解:1、实数域的紧密子集存在最大值和最小值 2、连续函数将紧密集映射为紧密集(利用柯西序列判 定) f ( ) x 为连续函数 D为紧密集

最优解的存在性 实数域的紧密子集存在最大值和最小值 1.紧密集为有界集,存在上下确界。 2.上、下确界属于紧密集 D=[-1,1] ①=R ①=(-1,1) ①=[-1,1]U[3,4] ①=[-1,0) D=[-1,1]∩Q 紧密集 无界不紧密集 有界不紧密集
实数域的紧密子集存在最大值和最小值 1.紧密集为有界集,存在上下确界。 2.上、下确界属于紧密集 D [ 1,1] D [ 1,1] D ( 1,1) D [ 1,1] [3, 4] D [ 1, ) D 紧密集 无界不紧密集 有界不紧密集

最优解的存在性 ,思考:下列最优解是否存在? f(x)=x2,x∈[0.01,1] f(x)=x2;x∈[-1,1]∩Q tno f(x)=x2,x∈(0.01,1] f(x)=-;x∈[-1,1] X
思考:下列最优解是否存在? 2 f x x x ( ) , 0.01,1 2 f x x x ( ) ; [ 1,1] 2 f x x x ( ) , (0.01,1] 2 ( ) ; [ 1,1] 4 f x x x 1 f x x ( ) ; [ 1,1] x

最优化问题 解的特点 问题转化 迭代法
最优化问题 解的特点 问题转化 迭代法
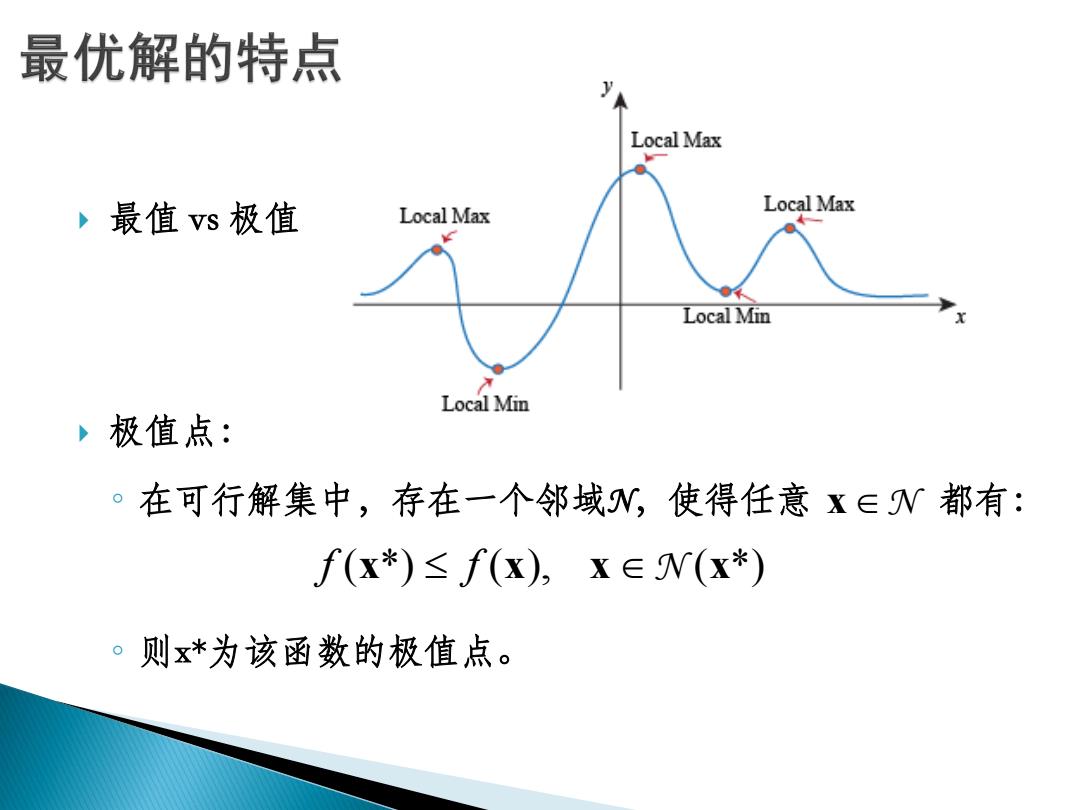
最优解的特点 Local Max ,最值vs极值 Local Max Local Max Local Min Local Min 极值点: 。在可行解集中,存在一个邻域N,使得任意x∈W都有: f(x*)≤f(x),X∈N(x*) 。则x*为该函数的极值点
最值 vs 极值 极值点: ◦ 在可行解集中,存在一个邻域N,使得任意 都有: ◦ 则x*为该函数的极值点。 xN f f ( *) ( ), ( *) x x x x N