
机器学习(Machine Learning) Machine Learning as a "Field of study that gives computers the ability to learn without being explicitly programmed" 阿瑟·塞缪尔(Arthur Machine Learning is the Samuel) scientific study of algorithms and statistical models that computer systems use to effectively perform a specific task without using explicit instructions. WIKIPEDIA
Machine Learning as a "Field of study that gives computers the ability to learn without being explicitly programmed". Machine Learning is the scientific study of algorithms and statistical models that computer systems use to effectively perform a specific task without using explicit instructions。 阿瑟·塞缪尔 (Arthur Samuel)
机器学习(Machine Learning) 机器是利用能量变换或传递能量、物质和信息的工具。 能量转化机 器一一内燃机 信息处理机 器一一计算机
机器是利用能量变换或传递能量、物质和信息的工具。 信息处理机 器——计算机 能量转化机 器——内燃机

“机器”建模 ,数学家眼中的信息处理机一一数学模型 。无论“机器”(分类器)结构如何复杂,分类器都可以表示 为一个多元单值函数:判决函数(discriminant function) f(x),R”→2 2={-11 。其中,定义域为特征空间,值域为类空间, 。几何模型: ·决策面(decision surface) f(x)=0
数学家眼中的信息处理机——数学模型 ◦ 无论“机器”(分类器)结构如何复杂,分类器都可以表示 为一个多元单值函数:判决函数(discriminant function) ◦ 其中,定义域为特征空间,值域为类空间, ◦ 几何模型: 决策面(decision surface) ( ), n f x { 1,1} f ( ) 0 x

“机器”建模 逼近论教程 ,分类函数的构造: 。如何得到分类函数? 。函数逼近理论: ⊙ ·把函数表示为一组基函数线性组合的形式: ·泰勒级数,傅立叶级数; f(x)=∑w,x f)=∑w,e2mf i=0,.,00
分类函数的构造: ◦ 如何得到分类函数? ◦ 函数逼近理论: 把函数表示为一组基函数线性组合的形式: 泰勒级数,傅立叶级数; 0,..., ( ) i i i f x w x 2 ,..., ( ) i j f t i i f t w e
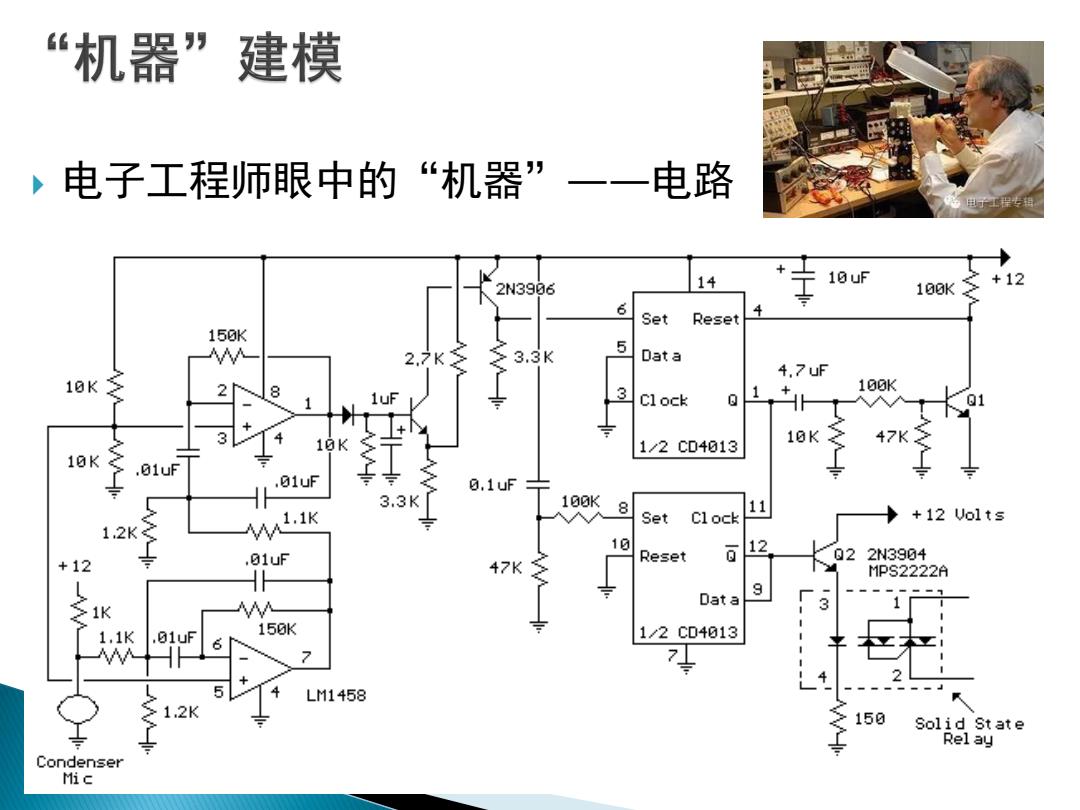
“机器”建模 ,电子工程师眼中的“机器”一一电路 10uF 2N3906 14 100K +12 6 Set Reset 150K 2.7K 3.3K 5 Data 18K 4.7uF 28 100K 1uF Clock 1 3 10K 1/2CD4013 10K 10K .01uf .01uF 0,1uF 3.3K 100K 8 11 1.1K Set Cl ock ◆+12Uo1ts 12K 10 +12 ,01uf Reset 石 12 022N3904 47K MPS2222A Data 9 1,1K .01uF 150K 1/2CD4013 6 7 7 4 5 LM1458 12K 150 Solid State Relay Condenser Mic
电子工程师眼中的“机器”——电路
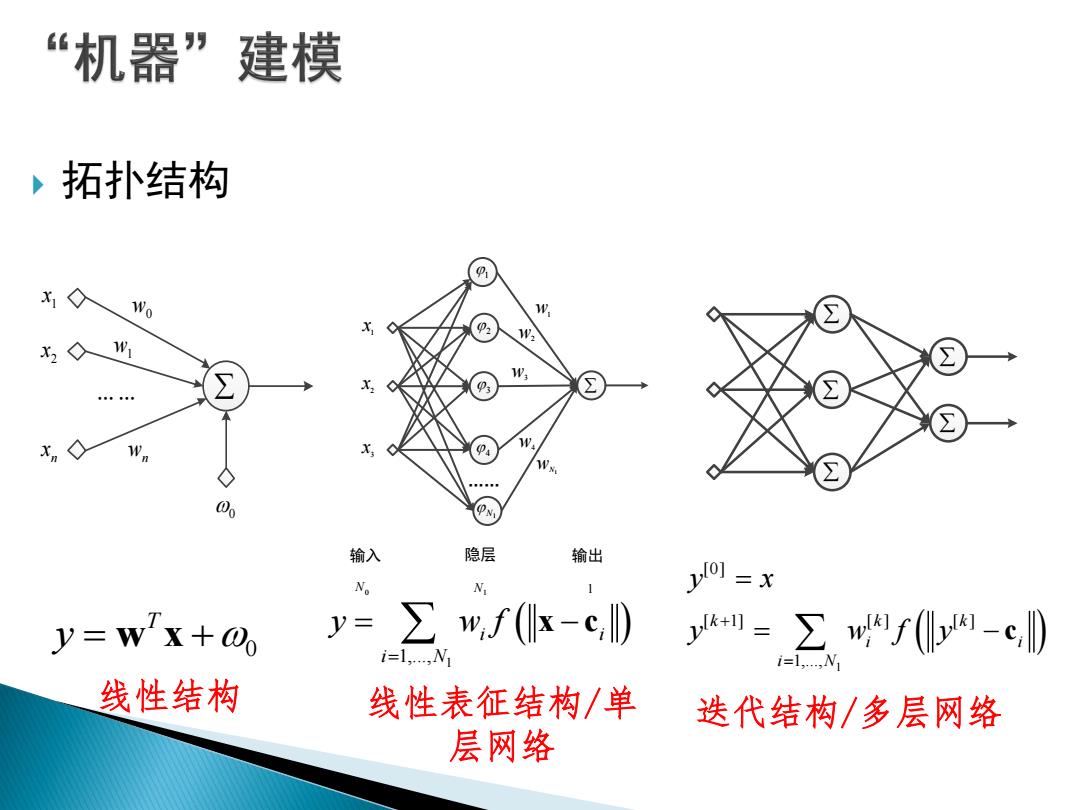
“机器”建模 拓扑结构 Wo W X2 191 ◇ Wa 06 输入 隐层 输出 N。 y[0]=x y-wx+@o y= ∑w,f(k-c) y=∑wf-cD i=1,,N1 i=1....N 线性结构 线性表征结构/单 迭代结构/多层网络 层网络
拓扑结构 1 x 2 x n x 0 w0 w1wn … … 0 T y w x x2 x1 x3 输入 隐层 输出 N0 N1 1 1 …… 2 3 4N1 w1 w2 w3w4wN1 1 1,..., i i i N y w f x c 1 [0] [ 1] [ ] [ ] 1,..., k k k i i i N y x y w f y c 线性结构 线性表征结构/单 层网络 迭代结构/多层网络

“机器”建模 软件工程师眼中的“机器”一一代码 D:work)■pt-mnist▣model〉2 model.py ▣Project 因÷在一 号model..py× release.py optExm D:\Haloes\gitHubloptExm 1 import torch.nn as nn >venv library root 2 import torch.nn.functional as F iopt-1.py External Libraries 3 D:\Haloes\gitHublopt 4 >Ill Extended Definitions 5 class Net(nn.Module): >Python36 library root 6 def_init_(self): >■DLs 7 #此处定义包含待训练权系数的模块 >Lib lli Binary Skeletons 8 super(Net,self)._init_() >venv library root 9 self.conv1 nn.Conv2d(1,10,kernel_size=3) 冫site-packages 10 self.conv2 nn.Conv2d(10,20,kerne1_size=3) )pip-10.0.1-py3.6.egg 11 self.fc1 nn.Linear(500,50) >setuptools-39.1.0-py3.6.egg library root 12 self.fc2 nn.Linear(50,10) >Ii Typeshed Stubs Scratches and Consoles 13 14 def forward(self,x): 15 x F.relu(F.max_pool2d(self.conv1(x),2)) 16 x F.relu(F.max_pool2d(self.conv2(x),2)) 17 x=x.view(-1,500》 18 x F.relu(self.fc1(x)) 19 x F.dropout(x,training=self.training)
软件工程师眼中的“机器”——代码
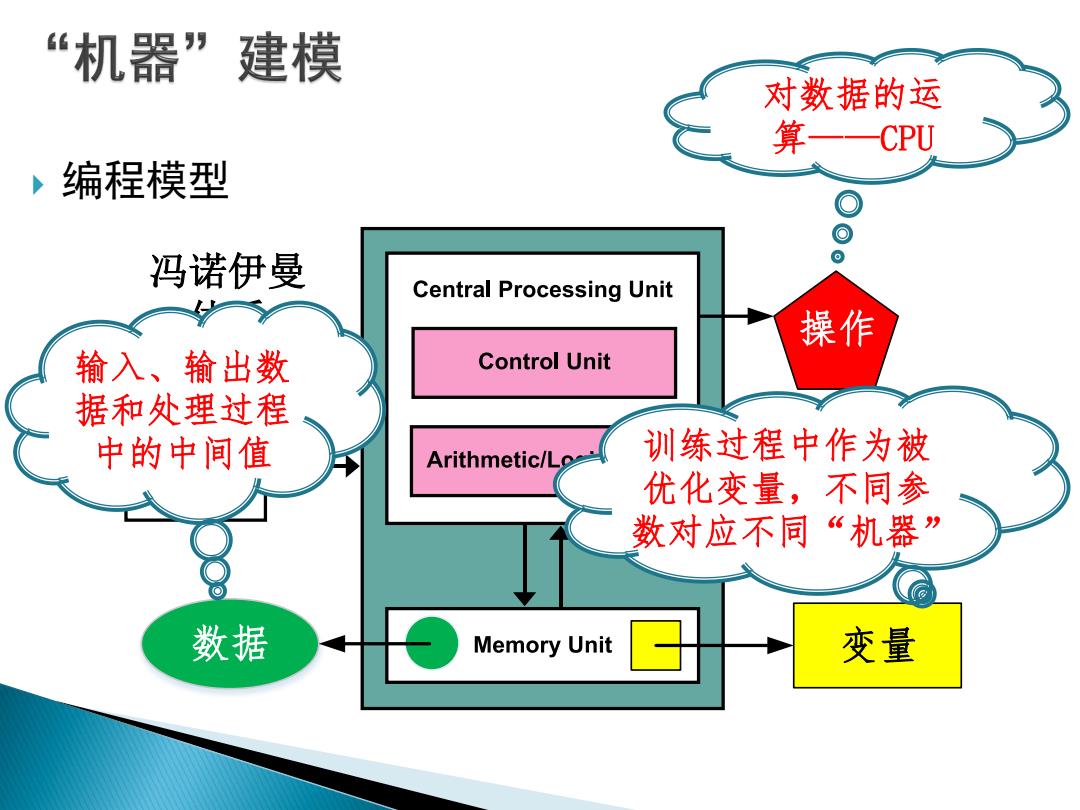
“机器”建模 对数据的运 算一CPU 编程模型 冯诺伊曼 Central Processing Unit 操作 输入、输出数 Control Unit 据和处理过程 中的中间值 Arithmetic/Lo 训练过程中作为被 优化变量,不同参 数对应不同“机器” 数据 Memory Unit 变量
编程模型 数据 变量 冯诺伊曼 体系 操作 对数据的运 算——CPU 训练过程中作为被 优化变量,不同参 数对应不同“机器” 输入、输出数 据和处理过程 中的中间值

“机器”的可塑性与学习 ,什么是“学习” 。不改变“学习主体”结构的情况下,通过调整其微观 参数,使其具有依据外部变化,自主优化响应的过程
什么是“学习” ◦ 不改变“学习主体”结构的情况下,通过调整其微观 参数,使其具有依据外部变化,自主优化响应的过程

“机器”的可塑性与学习 ,机器可塑性: 。保持机器结构不变情况下,通过改变其参数,可以改 变其响应特性。 。数学家:调整线性/非线性逼近的系数。 f(x,W),R”→2 。电子工程师:调整电路中元器件的物理量(电阻、电 容、寄存器等) 。软件工程师:调整程序中“变量”的值。 W+=W+△W
机器可塑性: ◦ 保持机器结构不变情况下,通过改变其参数,可以改 变其响应特性。 ◦ 数学家:调整线性/非线性逼近的系数。 ◦ 电子工程师:调整电路中元器件的物理量(电阻、电 容、寄存器等) ◦ 软件工程师:调整程序中“变量”的值。 ( ; ), n f x W W W W