
生态学实验
生态学实验

实验一、样方法调查种群数量及种群 内分布型的测定 一、实验目的 ❖ 通过实验,熟悉利用样方法调查种群数量 的基本原理,掌握该方法技术要点。 ❖ 通过实验,理解几种种群内分布型研究方 法的基本原理,掌握测定动物种群内分布型 的技术
实验一、样方法调查种群数量及种群 内分布型的测定 一、实验目的 ❖ 通过实验,熟悉利用样方法调查种群数量 的基本原理,掌握该方法技术要点。 ❖ 通过实验,理解几种种群内分布型研究方 法的基本原理,掌握测定动物种群内分布型 的技术

二、实验原理 ❖ 样方法是指在被调查种群的生存环境中, 随机选取若干个样方,计数每个样方内的个 体数,计算每个样方内的平均个体数,然后 将其平均数推广,来估计种群整体。 ❖ 样方的形状可以是方形的、长方形的、条 带状的或圆形的,但样方必须具有良好的代 表性,这可以通过随机取样来保证
二、实验原理 ❖ 样方法是指在被调查种群的生存环境中, 随机选取若干个样方,计数每个样方内的个 体数,计算每个样方内的平均个体数,然后 将其平均数推广,来估计种群整体。 ❖ 样方的形状可以是方形的、长方形的、条 带状的或圆形的,但样方必须具有良好的代 表性,这可以通过随机取样来保证

❖ 用样方法估计种群数量,首先要解决的问题是取多 少个样本比较好。在大多数情况下,样本数可以由 经验来决定。若生物个体集群分布,各样方个体数 离散程度较大,即数据的方差(S2)较大,则需抽 取的样方数较多;反之,若生物个体均匀分布,各 样方个体数离散程度较小,即数据的方差(S2)较 小,则需抽取的样方数较少。若要精确确定,可用 以下3种方法: 误差估计法 平均值滑动法 t值计算法
❖ 用样方法估计种群数量,首先要解决的问题是取多 少个样本比较好。在大多数情况下,样本数可以由 经验来决定。若生物个体集群分布,各样方个体数 离散程度较大,即数据的方差(S2)较大,则需抽 取的样方数较多;反之,若生物个体均匀分布,各 样方个体数离散程度较小,即数据的方差(S2)较 小,则需抽取的样方数较少。若要精确确定,可用 以下3种方法: 误差估计法 平均值滑动法 t值计算法
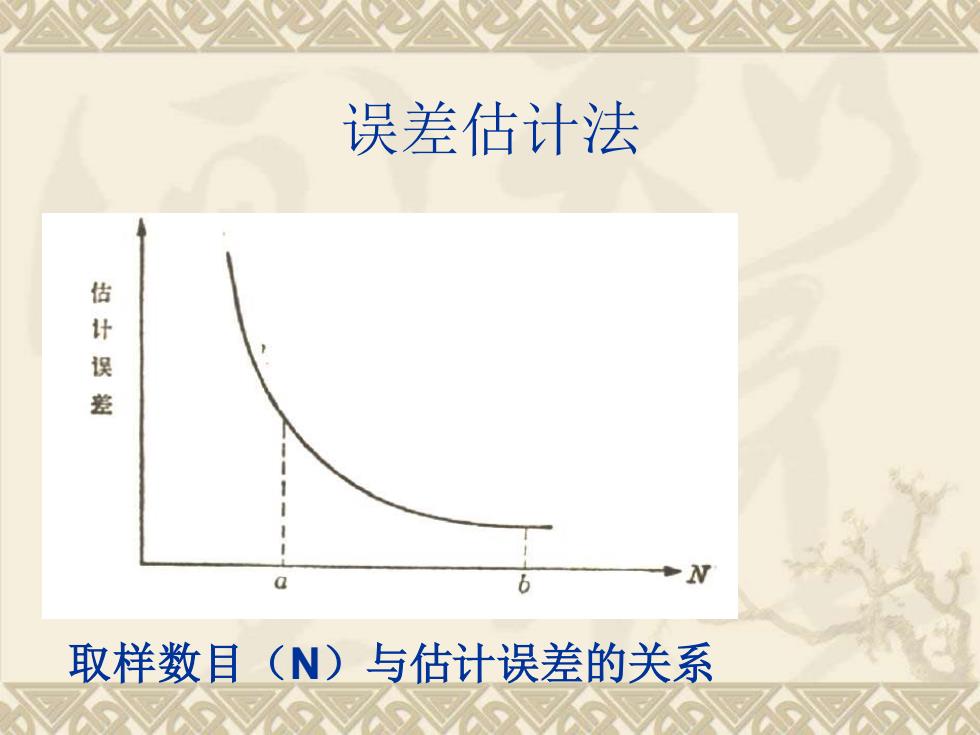
误差估计法 取样数目(N)与估计误差的关系
误差估计法 取样数目(N)与估计误差的关系
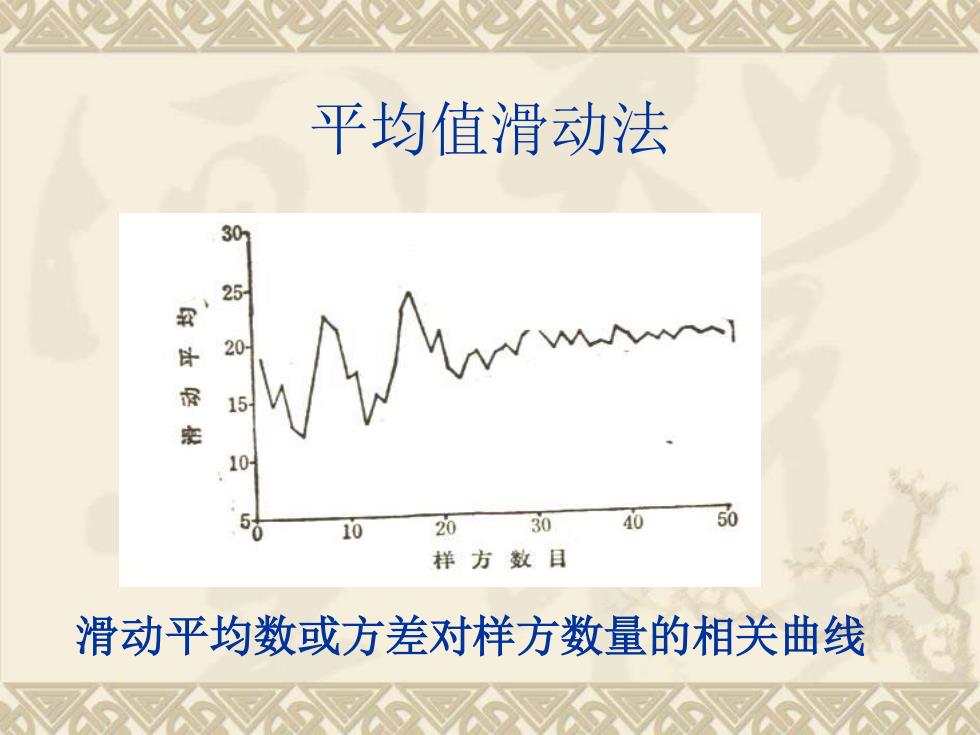
平均值滑动法 滑动平均数或方差对样方数量的相关曲线
平均值滑动法 滑动平均数或方差对样方数量的相关曲线

t值计算法 ❖ d为样本平均数的允许误差,可根据实验情况, 人为确定,如允许误差在10%以内;t可通过 查t值表得到,若样本数大于10,差异显著性 水平为5%时,t值约为2;σ2为总体方差,是 未知的,可用S2代替σ2 。 2 2 2 d t n =
t值计算法 ❖ d为样本平均数的允许误差,可根据实验情况, 人为确定,如允许误差在10%以内;t可通过 查t值表得到,若样本数大于10,差异显著性 水平为5%时,t值约为2;σ2为总体方差,是 未知的,可用S2代替σ2 。 2 2 2 d t n =

❖ 动物种群的内分布型主要决定于个体间的相 互作用和栖息环境的特点。动物种群中的个 体,彼此之间可能是相互吸引的,也可能是 相互排斥或中性的。若有机体彼此之间相互 吸引就会引起动物集群;相互排斥就会使个 体相互避开,就可能产生均匀的分布;而中 性关系就可能促成随机分布。如果资源(如 食物、营巢地等)是丰富且分布均匀的,动 物种群就可能会出现随机分布,甚至出现均 匀分布;如果资源呈斑块状分布,就可能导 致动物种群集群分布
❖ 动物种群的内分布型主要决定于个体间的相 互作用和栖息环境的特点。动物种群中的个 体,彼此之间可能是相互吸引的,也可能是 相互排斥或中性的。若有机体彼此之间相互 吸引就会引起动物集群;相互排斥就会使个 体相互避开,就可能产生均匀的分布;而中 性关系就可能促成随机分布。如果资源(如 食物、营巢地等)是丰富且分布均匀的,动 物种群就可能会出现随机分布,甚至出现均 匀分布;如果资源呈斑块状分布,就可能导 致动物种群集群分布

❖ 种群的内分布型的研究属于静态研究,比较 适用于植物、定居或不太活动的动物,也适 用于测量鼠穴、鸟巢等栖息地的空间分布。 测定种群内分布型的方法很多,本实验仅介 绍以下三种方法。 方差/平均数比率法 泊松(Poisson)分布法 负二项式分布法
❖ 种群的内分布型的研究属于静态研究,比较 适用于植物、定居或不太活动的动物,也适 用于测量鼠穴、鸟巢等栖息地的空间分布。 测定种群内分布型的方法很多,本实验仅介 绍以下三种方法。 方差/平均数比率法 泊松(Poisson)分布法 负二项式分布法
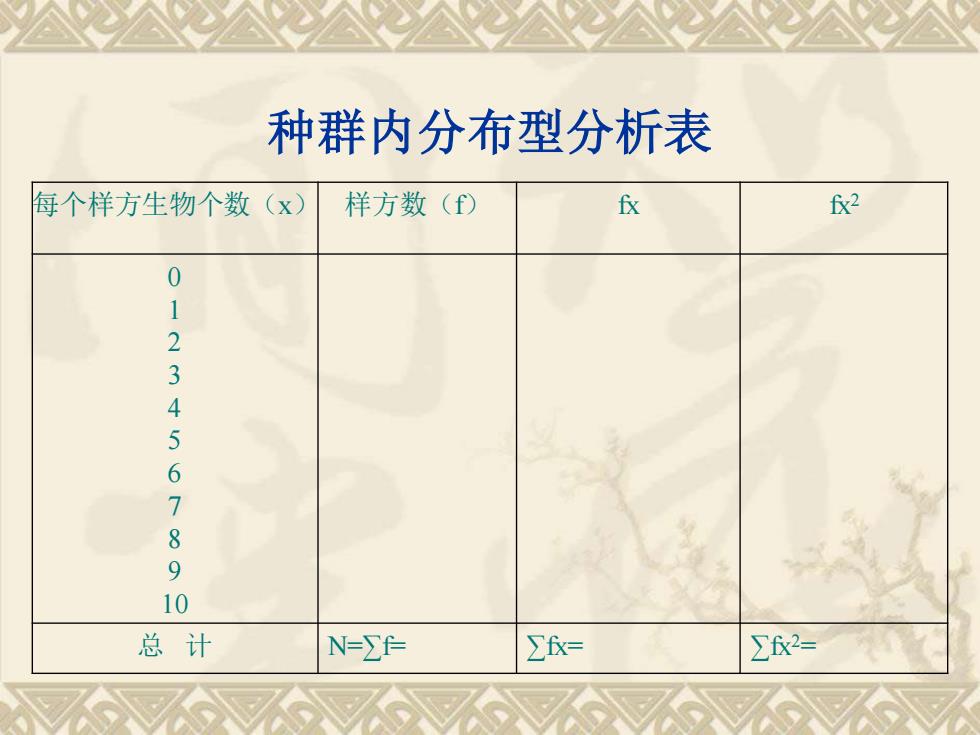
种群内分布型分析表 每个样方生物个数(x) 样方数(f) fx fx2 0 1 2 3 4 5 6 7 8 9 10 总 计 N=∑f= ∑fx= ∑fx2=
种群内分布型分析表 每个样方生物个数(x) 样方数(f) fx fx2 0 1 2 3 4 5 6 7 8 9 10 总 计 N=∑f= ∑fx= ∑fx2=