
第三章 光场的二阶相干性基础
第三章 光场的二阶相干性基础

本章为容Contents ○3.1光的时间相千性 ●3.2准单色光的千涉 ©3.3光的空间相千性 ●3.4二阶相千性的基本描述 ●3.5典型相千实验的数学描述 ○3.6准单色条件
Contents 3.2 准单色光的干涉 3.6 准单色条件 3.1 光的时间相干性 3.5 典型相干实验的数学描述 3.4 二阶相干性的基本描述 3.3 光的空间相干性

g3-1 光的时间相干性
3-1

1、相干性的宏观现象 在杨氏干涉实验中,当用不同波长的光照明单孔,或使用 多色光的点光源时,各个波长均会各自产生一组干涉条纹, 各组干涉条纹的间距不同。干涉场中各点的总光强就应是 各个单色图样的强度之和。 不同波长的第m级条纹将错开的距离为: 对于准单色光: 4 <1 A
1、相干性的宏观现象 在杨氏干涉实验中,当用不同波长的光照明单孔,或使用 多色光的点光源时,各个波长均会各自产生一组干涉条纹, 各组干涉条纹的间距不同。干涉场中各点的总光强就应是 各个单色图样的强度之和。 mD l d 对于准单色光: 1 O 不同波长的第m级条纹将错开的距离为: x
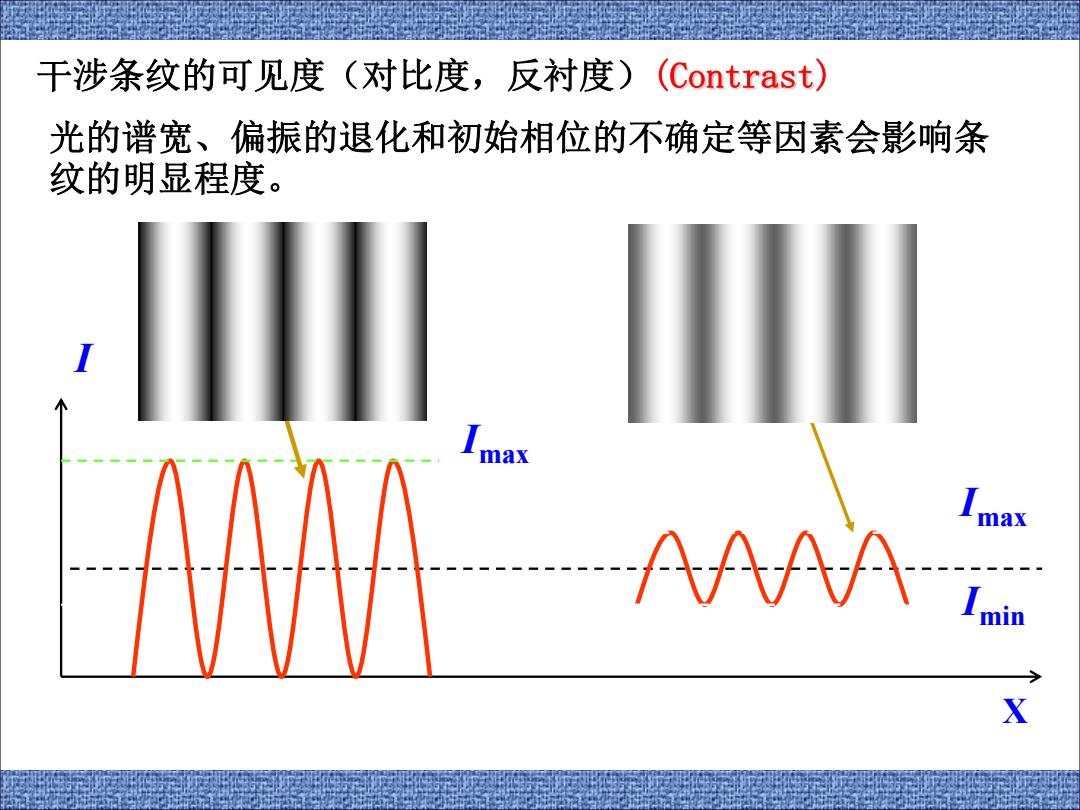
干涉条纹的可见度(对比度,反衬度)(Contrast) 光的谱宽、偏振的退化和初始相位的不确定等因素会影响条 纹的明显程度。 max AA max X
X I Imin Imax Imax 干涉条纹的可见度(对比度,反衬度)(Contrast) 光的谱宽、偏振的退化和初始相位的不确定等因素会影响条 纹的明显程度

条纹的可见度: V= max min 描述干涉现象的明显程度 max + min 对于两光束干涉: ∫1mx=(A+4)月 11=(4-4)月 (A+A)2-(A-A)2 (4+A)2+(4-A)P A 1+ A 2A1A2 1+ A (A2+A22) A
条纹的可见度: max min max min I I V I I 描述干涉现象的明显程度 2 max 1 2 I (A A ) 2 min 1 2 I (A A ) 1 2 2 1 2 1 2 2 2 2 2 1 2 1 2 1 2 2 ( ) ( ) ( ) ( ) 1 A A A A A A V A A A A A A 1 2 1 2 2 2 2 1 1 2 2 2 2 ( ) 1 A A A A V A A A A 对于两光束干涉:

▲I=A2+A,2+2AA2c0s△p V= 244 (A2+A22) =A2+A2+V(42+A2)cos△0 令1。=1+5=4+42 I=I(1+Vcos△p) ▲决定可见度的因素: 振幅比,光源的单色性,光源的空间宽度等
▲ 2 1 2 cos 2 2 2 I A1 A A A 1 2 2 2 1 2 2 ( ) A A V A A 2 2 2 2 1 2 1 2 A A V A A ( )cos 0 I I V (1 cos ) 令 2 2 0 1 2 1 2 I I I A A ▲ 决定可见度的因素: 振幅比, 光源的单色性, 光源的空间宽度等
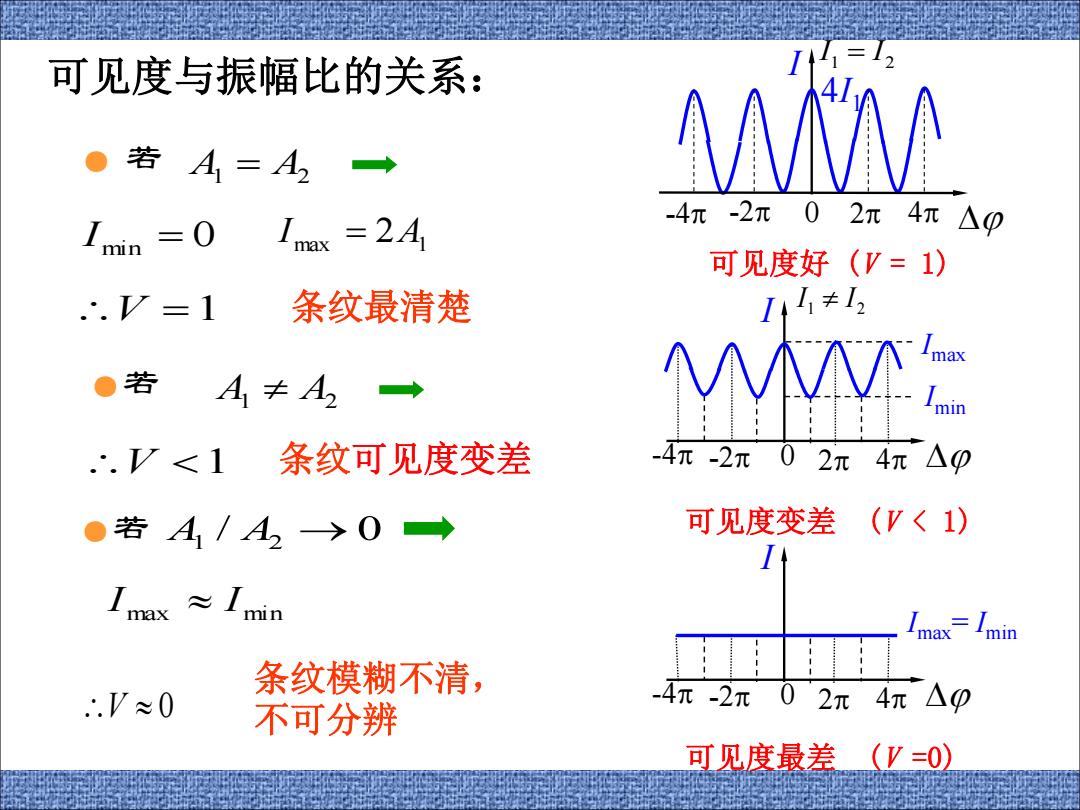
可见度与振幅比的关系: ●若A1=A2→ △A Imax =24 -4π-2π Imin =0 02π4π△0 可见度好(V=1) .∴.=1 条纹最清楚 1 ●若 A≠A2→ 个 ..V0→ 可见度变差(V〈1) ≈Imin max /min 条纹模糊不清, .V≈0 -4π-2元02元4π △0 不可分辨 可见度最差(V=0)
● 若 A1 A2 I min 0 max 2A1 I V 1 条纹最清楚 ● 若 1 2 A A/ 0 max min I I 1 2 I I I -4 -2 0 2 4 4I1 可见度好 (V = 1) 1 2 I I I Imax Imin -4 -2 0 2 4 可见度变差 (V < 1) ● 若 A1 A2 V 1 条纹可见度变差 可见度与振幅比的关系: I Imax= Imin -4 -2 0 2 4 可见度最差 (V =0) V 0 条纹模糊不清, 不可分辨
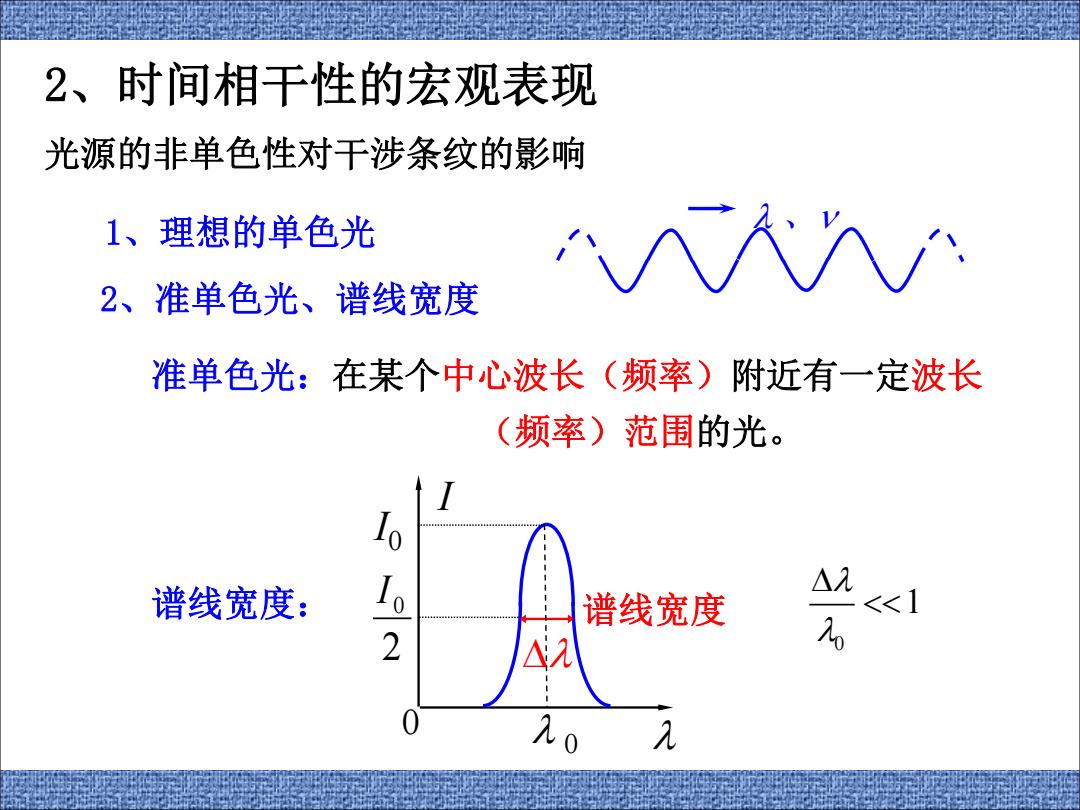
2、时间相干性的宏观表现 光源的非单色性对干涉条纹的影响 1、理想的单色光 2、准单色光、谱线宽度 准单色光:在某个中心波长(频率)附近有一定波长 (频率)范围的光。 谱线宽度: o 谱线宽度 <<1 2 △2 20
1、理想的单色光 、 2、准单色光、谱线宽度 谱线宽度: 准单色光:在某个中心波长(频率)附近有一定波长 (频率)范围的光。 0 0 I I0 谱线宽度 2 0 I 2、时间相干性的宏观表现 光源的非单色性对干涉条纹的影响 0 1

造成谱线宽度的原因: 自然宽度(由能级的宽度造成) E △E,+AE, △V= h E △E, 多普勒增宽 △ycV, 碰撞增宽 AVxz∝p(T-定),p→△v
● 自然宽度(由能级的宽度造成) Ej Ei Ei h Ei Ej 造成谱线宽度的原因: ● 多普勒增宽 v ● 碰撞增宽 p v, z p (T一定), Ej ·