
University of Electronic Science and Technology of China 956 三.条形光波导一结构与分析 1
University of Electronic Science and Technology of China 1 三.条形光波导—结构与分析

University of Electronic Science and Technology of China 956 口条形光波导简介 平板波导对光仅能提供一个方向的约束。 条形光波导则能在水平与竖直两个方向上对其中传输 的光波进行约束。 绝大多数商用的光波导器件,例如,光波导开关、电 光调制器、波导分束器都是由条形光波导构成。 有必要了解并掌握条形光波导的基本传输特性,为此 需要建立其色散方程。 2
University of Electronic Science and Technology of China 2 ❑条形光波导简介 • 平板波导对光仅能提供一个方向的约束。 • 条形光波导则能在水平与竖直两个方向上对其中传输 的光波进行约束。 • 绝大多数商用的光波导器件,例如,光波导开关、电 光调制器、波导分束器都是由条形光波导构成。 • 有必要了解并掌握条形光波导的基本传输特性,为此 需要建立其色散方程
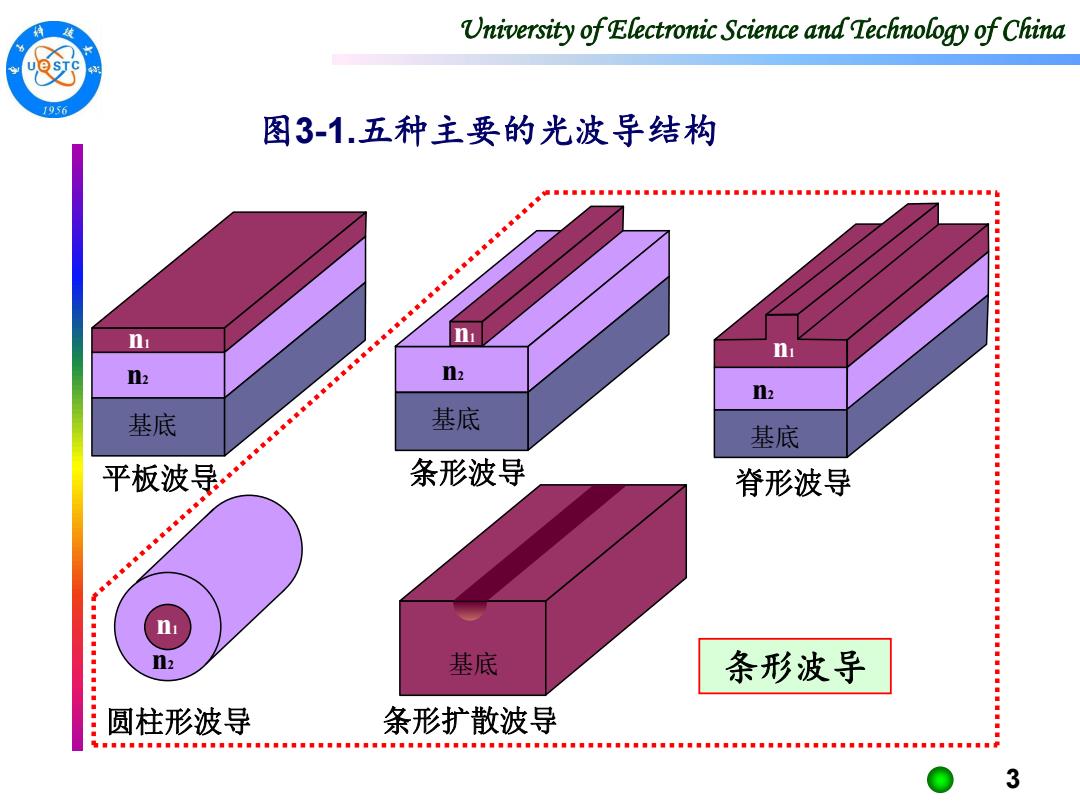
University of Electronic Science and Technology of China 956 图3-1.五种主要的光波导结构 ■ 骏 n: ni n2 n2 n2 基底 基底 基底 条形波导 脊形波导 ni 基底 条形波导 圆柱形波导 条形扩散波导 hg■gg■■■gg”g■9■■8g■g■g9■■g””目■0■g■■0目■■g■■■gg■g。■■■g■■gg■”■■■■ggg■■■■■gg”g■g0g。g■g目■■■■g”g■■8gg■■gF 3
University of Electronic Science and Technology of China 3 平板波导 圆柱形波导 基底 条形波导 基底 脊形波导 基底 n2 n n2 2 n2 n1 n1 n1 n1 条形扩散波导 基底 图3-1.五种主要的光波导结构 条形波导

University of Electronic Science and Technology of China 956 口条形光波导简介 在对条形光波导进行分析时,一般作如下近似: ① 弱导近似 既是 m1-1<1,(i=2,3,4,5) ny n1-波导芯层折射率,n;-包层各区域折射率。 通常情况下,实际的光波导都满足此条件的。 4
University of Electronic Science and Technology of China 4 ❑条形光波导简介 在对条形光波导进行分析时,一般作如下近似: ① 弱导近似 既是 1, ( 2,3,4,5) 1 1 = − i n n ni n1 ---波导芯层折射率,ni ---包层各区域折射率。 通常情况下,实际的光波导都满足此条件的

University of Electronic Science and Technology of China 956 ② 准TEM近似 在弱导近似下,可以证明,条形光波导中导模的场量的 纵向分量比横向分量要小很多,其中传输的光波模式不 是纯粹的TE模或TM模,而是TEM模,这种光波模式的 电磁特征可分为以下两类: 表示 主要分量 较小分量 最小分量 Erin 横向的E,H 纵向的E,H 横向的E、 E别 n 横向的E,H纵向的E,H 横向的Ex x,y-模式的电场偏振方向,m,n-模式序数。 TEM模→固定的偏振方向→标量模→线偏振模 5
University of Electronic Science and Technology of China 5 ② 准TEM近似 在弱导近似下,可以证明,条形光波导中导模的场量的 纵向分量比横向分量要小很多,其中传输的光波模式不 是纯粹的TE模或TM模,而是TEM模,这种光波模式的 电磁特征可分为以下两类: Ex H y , 横向的 纵向的 横向的 横向的 纵向的 横向的 表示 主要分量 较小分量 最小分量 横向的 纵向的 横向的 横向的 纵向的 横向的 表示 主要分量 较小分量 最小分量 x Emn y Emn Ey Hx , Ez Hz , Ez Hz , Ey Ex x,y --模式的电场偏振方向,m,n--模式序数。 TEM模→固定的偏振方向→标量模→线偏振模

University of Electronic Science and Technology of China 1956 口条形光波导的分析方法虽然都是基于麦克斯韦方程组 和边界条件,但根据求解方式的不同基本上可分为两类, 其一为近似解法,其二为数值解法。 口数值解法主要有束传播法(BPM)、有限元法(FEM)、有 限差分法(FDM)、有限差分时域法(FDTDM)等,对应这 些方法的成熟的商用的软件也已经推出。数值解法可以 形象地将波导中光波的传播及模场分布展示出来,但不 能揭示其中的物理实质,而且其结果严重依赖于建模的 准确性。 6
University of Electronic Science and Technology of China 6 ❑ 条形光波导的分析方法虽然都是基于麦克斯韦方程组 和边界条件,但根据求解方式的不同基本上可分为两类, 其一为近似解法,其二为数值解法。 ❑数值解法主要有束传播法(BPM)、有限元法(FEM)、有 限差分法(FDM)、有限差分时域法(FDTDM)等,对应这 些方法的成熟的商用的软件也已经推出。数值解法可以 形象地将波导中光波的传播及模场分布展示出来,但不 能揭示其中的物理实质,而且其结果严重依赖于建模的 准确性
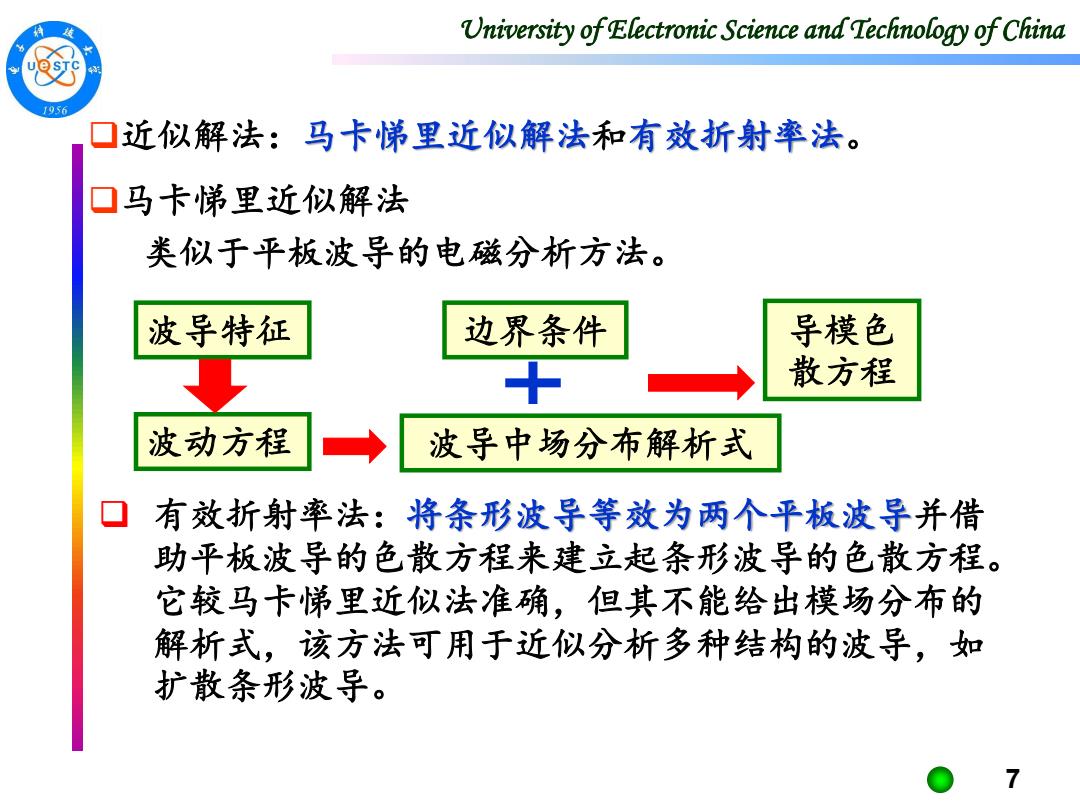
University of Electronic Science and Technology of China 956 近似解法:马卡悌里近似解法和有效析射率法。 口马卡悌里近似解法 类似于平板波导的电磁分析方法。 波导特征 边界条件 导模色 散方程 波动方程 波导中场分布解析式 有效折射率法:将条形波导等效为两个平板波导并借 助平板波导的色散方程来建立起条形波导的色散方程。 它较马卡悌里近似法准确,但其不能给出模场分布的 解析式,该方法可用于近似分析多种结构的波导,如 扩散条形波导。 7
University of Electronic Science and Technology of China 7 ❑近似解法:马卡悌里近似解法和有效折射率法。 ❑马卡悌里近似解法 类似于平板波导的电磁分析方法。 波导特征 波动方程 波导中场分布解析式 边界条件 导模色 散方程 ❑ 有效折射率法:将条形波导等效为两个平板波导并借 助平板波导的色散方程来建立起条形波导的色散方程。 它较马卡悌里近似法准确,但其不能给出模场分布的 解析式,该方法可用于近似分析多种结构的波导,如 扩散条形波导

University of Electronic Science and Technology of China 956 口本章内容 1.分析矩形波导的马卡悌里(Marcatili)近似方法 2.分析矩形波导的库玛(Kumar)方法 3.分析矩形波导的有效折射率方法 4. 【例】有效折射率方法分析脊形波导 5.【例】有效析射率方法分析条形扩散波导 8
University of Electronic Science and Technology of China 8 ❑本章内容 1. 分析矩形波导的马卡悌里(Marcatili)近似方法 2. 分析矩形波导的库玛(Kumar)方法 3. 分析矩形波导的有效折射率方法 4. 【例】有效折射率方法分析脊形波导 5. 【例】有效折射率方法分析条形扩散波导
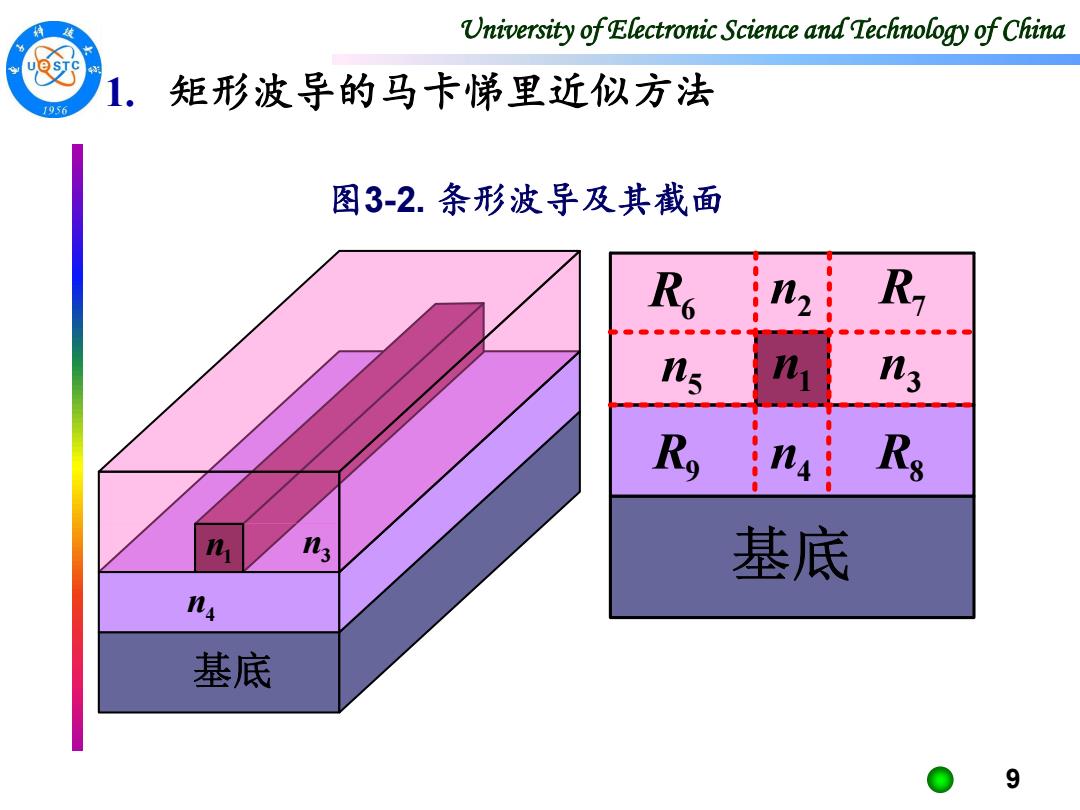
University of Electronic Science and Technology of China 1.矩形波导的马卡悌里近似方法 1956 图3-2.条形波导及其截面 n3 Rs n 基底 n 基底 9
University of Electronic Science and Technology of China 9 1. 矩形波导的马卡悌里近似方法 图3-2. 条形波导及其截面 基底 n4n1 n3 基底 n4 n1 n3 n2 n5 R6 R7 R9 R8

University of Electronic Science and Technology of China 1. 矩形波导的马卡悌里近似方法 各种条形波导的严格解法应该是在图3-2所示的9个区域 内分别列出场函数,然后利用所有界面上的边界条件, 求出相应导模的传播常数B及所对应的场函数,但这样的 求解是十分困难的。 马卡悌里考虑到,通常实际的光波导是工作在远离截止 点(?)的,这种情形下,光场高度集中在波导芯区, 透入2,3,4,5四个区域的能量是很少的,而阴影区域6,7,8,9 等四个角的光场则可忽略不计,这样就使得问题大大简 化。 请参阅: Ref.1 E.A.J.Marcatili,"Dielectric Rectangular Waveguide and Directional Coupler for Integrated Opuics,"Bell.Syst.Tech.J.Vol.48,No.7,pp. 2071-2102,1969. 10
University of Electronic Science and Technology of China 10 1. 矩形波导的马卡悌里近似方法 ❑ 各种条形波导的严格解法应该是在图3-2所示的9个区域 内分别列出场函数,然后利用所有界面上的边界条件, 求出相应导模的传播常数及所对应的场函数,但这样的 求解是十分困难的。 ❑ 马卡悌里考虑到,通常实际的光波导是工作在远离截止 点(?)的,这种情形下,光场高度集中在波导芯区, 透入2,3,4,5四个区域的能量是很少的,而阴影区域6,7,8,9 等四个角的光场则可忽略不计,这样就使得问题大大简 化。 请参阅: Ref. 1 E. A. J. Marcatili, “Dielectric Rectangular Waveguide and Directional Coupler for Integrated Opücs," Bell. Syst. Tech. J. Vol. 48, No. 7, pp. 2071-2102, 1969