例1-1设一杆沿轴线同时受力B,卫,乃的作用,其作用点分别为A、C、B,如图1-l 求杆的轴力。 P2-3kN2 P1=2kN P3=1kN (a) Pi=2kN P:-2kN P2-3N (b) 例图1-1 解:由于杆上有三个外力,因此在AC段和CB段的横截面上将有不同的轴力。 (1)在4C段内的任意处以横截面11将杆截为两段,取左段为研究对象,将右段对左段 的作用以内力N,代替(图1-1b)。由平衡条件知N,必与杆的轴线重合,方向与P相反,为拉 力,由平衡方程 ΣX=0,N1-P=0 N,=P =2kN 这就是AC段内任一横截面上的内力。 (2)再在CB段内的任意处以横截面2-2将杆截开,仍取左段为研究对象。此时因截面2 2上内力N2的方向一时不易确定,可将N2先设为拉力,如图1-lc所示,再由平衡方程 ΣX=0,N2-+=0 得 N,=P-E=2-3=-1kN 计算结果中的负号说明,该截面上内力的方向应与假设的方向相反,即八,为压力,其值为 IkN。此即CB段内任一横截面上的内力。 以上的计算,都是选取左段为研究对象,如果选取右段为研究对象,仍可得到同样的结果。 要点与讨论 直杆任一横截面上轴力,等于截面任意一侧杆段所受轴向外力的代数和。 例21试求图21中所示各杆在截面1-1、2-2、3-3上的轴力,并作轴力图
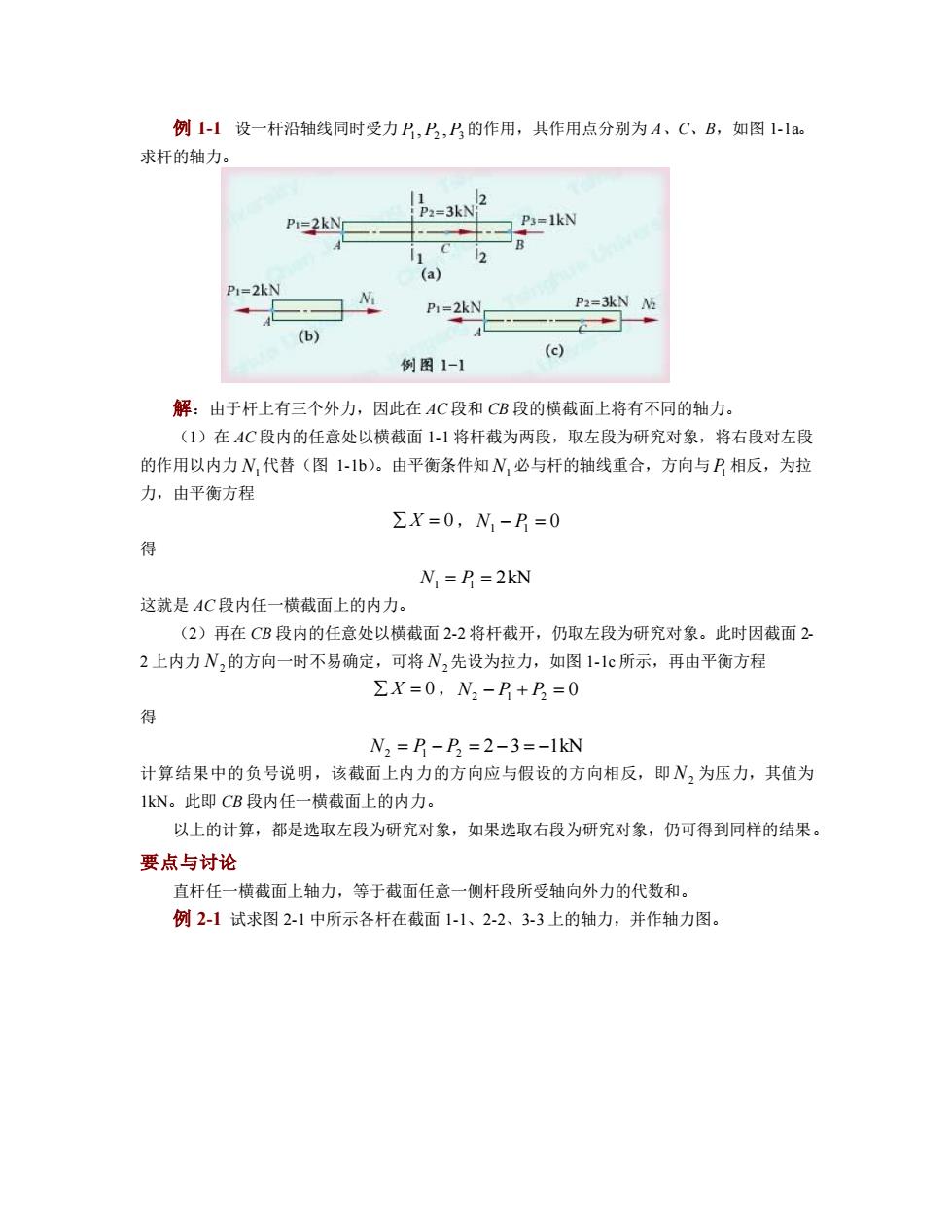
例 1-1 设一杆沿轴线同时受力 1 2 3 P , P ,P 的作用,其作用点分别为 A、C、B,如图 1-1a。 求杆的轴力。 解:由于杆上有三个外力,因此在 AC 段和 CB 段的横截面上将有不同的轴力。 (1)在 AC 段内的任意处以横截面 1-1 将杆截为两段,取左段为研究对象,将右段对左段 的作用以内力 N1 代替(图 1-1b)。由平衡条件知 N1 必与杆的轴线重合,方向与 P1 相反,为拉 力,由平衡方程 X = 0 , N1 − P1 = 0 得 N1 = P1 = 2kN 这就是 AC 段内任一横截面上的内力。 (2)再在 CB 段内的任意处以横截面 2-2 将杆截开,仍取左段为研究对象。此时因截面 2- 2 上内力 N2 的方向一时不易确定,可将 N2 先设为拉力,如图 1-1c 所示,再由平衡方程 X = 0 , N2 − P1 + P2 = 0 得 N2 = P1 − P2 = 2 −3 = −1kN 计算结果中的负号说明,该截面上内力的方向应与假设的方向相反,即 N2 为压力,其值为 1kN。此即 CB 段内任一横截面上的内力。 以上的计算,都是选取左段为研究对象,如果选取右段为研究对象,仍可得到同样的结果。 要点与讨论 直杆任一横截面上轴力,等于截面任意一侧杆段所受轴向外力的代数和。 例 2-1 试求图 2-1 中所示各杆在截面 1-1、2-2、3-3 上的轴力,并作轴力图
解:(1)求各截面轴力 截面11由左段(图b)的平衡条件 -(a) ΣX=0,N1=0 截面2-2由左段(图c)的平衡条件 6) ΣX=0,N2=2P(拉) (c) 截面3-3由左段(图d)的平衡条件 ∑X=0,N3=2P-P=P(拉) (2)作轴力图 由所得各截面的轴力,可作杆的轴力图 2外 (e) 如图e所示。 例图2-1 要点与讨论 1.在求杆件的轴力时,一般应先计算杆件的未知外力(包括支座反力)。 2.在本题中,若始终取截面的左段来考虑,则可不求A端支座反力。 例2-2图2-2所示较接正方形结构,各杆的横截面面积都等于25cm2,材料均为铸铁,其 许用拉应力[o,]=35MNm2,许用压应力口,=150MNhm',试求结构的许可载荷。 解:(1)求各杆轴力 由节点B(图2-2b)的平衡 条件 ∑X=0 P-2N1cos45°=0, (b) 例图2-2 由节点A(图2-2c)的平衡条件 N2-2N1cos45°=0,N2=P(压) (2)许可载荷 由斜杆的拉伸强度条件 所以 P≤24[o,]=V2×25×10)x35x10)=123.7kN 由铅垂杆的压缩强度条件
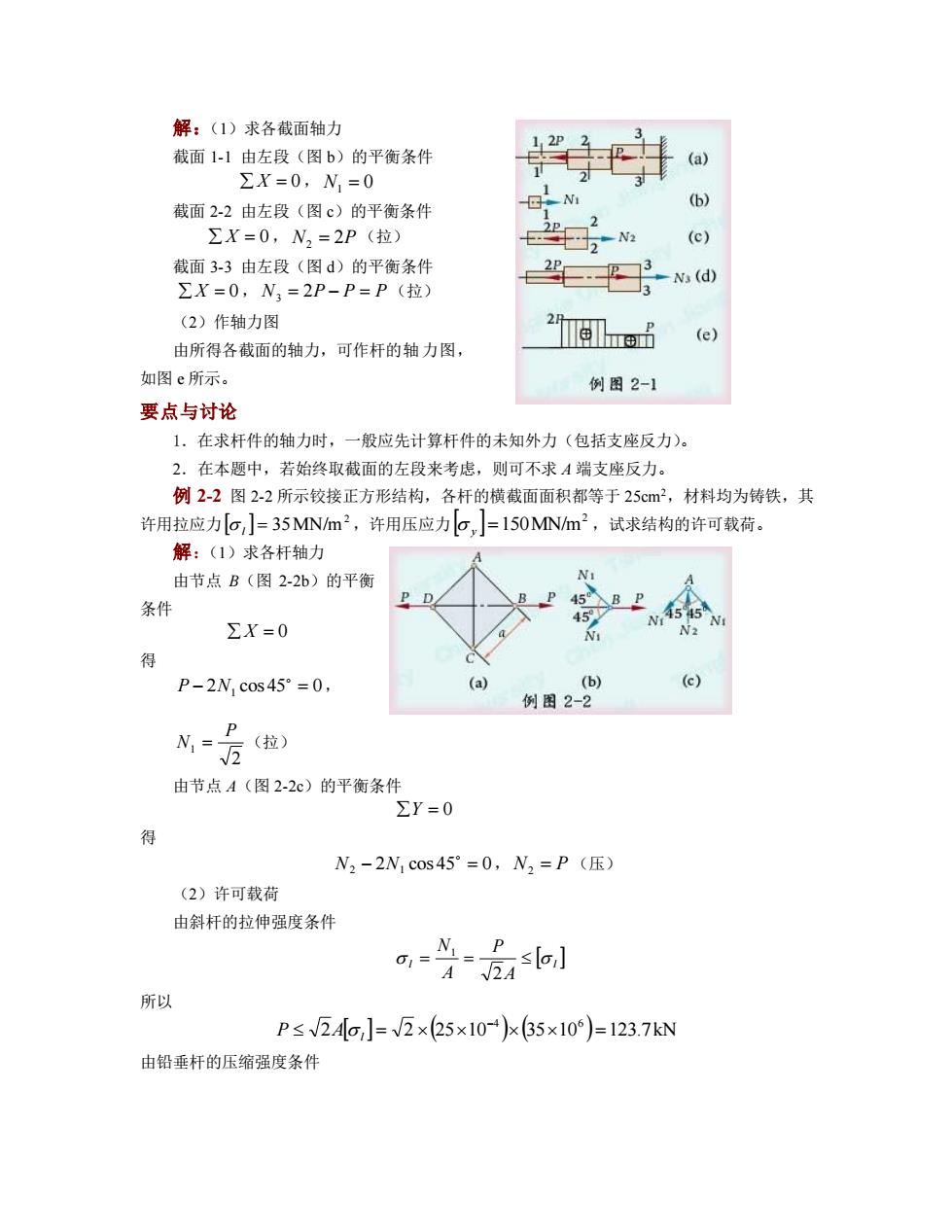
解:(1)求各截面轴力 截面 1-1 由左段(图 b)的平衡条件 X = 0 , N1 = 0 截面 2-2 由左段(图 c)的平衡条件 X = 0, N2 = 2P (拉) 截面 3-3 由左段(图 d)的平衡条件 X = 0, N3 = 2P − P = P (拉) (2)作轴力图 由所得各截面的轴力,可作杆的轴力图, 如图 e 所示。 要点与讨论 1.在求杆件的轴力时,一般应先计算杆件的未知外力(包括支座反力)。 2.在本题中,若始终取截面的左段来考虑,则可不求 A 端支座反力。 例 2-2 图 2-2 所示铰接正方形结构,各杆的横截面面积都等于 25cm2,材料均为铸铁,其 许用拉应力 MN/m2 l = 35 ,许用压应力 MN/m2 y =150 ,试求结构的许可载荷。 解:(1)求各杆轴力 由节点 B(图 2-2b)的平衡 条件 X = 0 得 − 2 1 cos45 = 0 P N , 2 1 P N = (拉) 由节点 A(图 2-2c)的平衡条件 Y = 0 得 2 − 2 1 cos 45 = 0 N N , N2 = P (压) (2)许可载荷 由斜杆的拉伸强度条件 l l A P A N = = 2 1 所以 2 2 (25 10 ) (35 10 ) 123.7kN 4 6 = = − P A l 由铅垂杆的压缩强度条件

as 所以 P≤A4ol=25x10-+)x35x105)=375kN 故结构的许可载荷为[P]=123.7kN 要点与讨论 1,尽管拉力N,要比压力N,小约40%,但结构的许可载荷还是受拉伸强度所限制。这是 因为铸铁的抗拉强度要比其抗压强度低得多。 2.在工程实际中,受压构件通常选用铸铁等脆性材料,而受拉构件一般选用低碳钢等塑 性材料,以合理地利用各种材料的机械性能。 例23图23所示结构,杆AB和BC的抗拉刚度EA相同,在节点B处承受集中载荷P, 试求节点B的水平及铅垂位移。 解:(1)求各杆轴力 由节点B(图2-3b)的平衡 条件 ΣX=0,ΣY=0 人45 N2cos45°-N,=0 N2sin45°-P=0 解得 (a) N1=P,N2=√2P B45 N (2)求各杆变形 杆AB (b) 杆BC 例图2-3 N.-Nh=VpxVa_2Pa EA EA (伸长) (3)节点B的位移 结构变形后,两杆仍应相交在一点,这就是变形的相容条件,作结构的变形图(图2-3c): 沿杆AB的延长线量取BB:等于△,沿杆CB的延长线量取BB2等于M2,分别在点B1和处 作BB,和BB,的垂线,两垂线的交点B'为结构变形后节点B应有的新位置。也即,结构变形后 成为AB'C的形状。图2-3c称为结构的变形图。 为求节点B的位移,也可单独作出节点B的位移图。位移图的作法与变形图作法类似,如 图2-3d所示
y A P A N = = 2 2 所以 (25 10 ) (35 10 ) 375kN 4 6 = = − P A y 故结构的许可载荷为 P =123.7kN 要点与讨论 1.尽管拉力 N1 要比压力 N2 小约 40%,但结构的许可载荷还是受拉伸强度所限制。这是 因为铸铁的抗拉强度要比其抗压强度低得多。 2.在工程实际中,受压构件通常选用铸铁等脆性材料,而受拉构件一般选用低碳钢等塑 性材料,以合理地利用各种材料的机械性能。 例 2-3 图 2-3 所示结构,杆 AB 和 BC 的抗拉刚度 EA 相同,在节点 B 处承受集中载荷 P, 试求节点 B 的水平及铅垂位移。 解:(1)求各杆轴力 由节点 B(图 2-3b)的平衡 条件 X = 0, Y = 0 得 N2 cos 45 − N1 = 0 N2 sin 45 − P = 0 解得 N1 = P, N2 = 2P (2)求各杆变形 杆 AB EA Pa EA N l l = = 1 1 1 (伸长) 杆 BC EA Pa EA P a EA N l l 2 2 2 2 2 2 = = = (伸长) (3)节点 B 的位移 结构变形后,两杆仍应相交在一点,这就是变形的相容条件,作结构的变形图(图 2-3c): 沿杆 AB 的延长线量取 BB1 等于 1 l ,沿杆 CB 的延长线量取 BB2等于 2 l ,分别在点 B1和B2处 作 BB1 和 BB2的垂线,两垂线的交点 B 为结构变形后节点 B 应有的新位置。也即,结构变形后 成为 ABC 的形状。图 2-3c 称为结构的变形图。 为求节点 B 的位移,也可单独作出节点 B 的位移图。位移图的作法与变形图作法类似,如 图 2-3d 所示

结构的变形图和节点的位移图,在计算节点位移中是等价的。在今后的计算中,可根据具 体情况,选作一图。 由位移图的几何关系,可得 水平位移 =照=出-留) 铅垂位移 名g+如59}会=62贤山 P4=BB=△ 要点与讨论 1.在载荷P作用下,由于两杆长度改变,导致节点B发生位移,两杆方位改变,夹角不 再为45°,如果按45°求解,则两杆的轴力之值与实际数值尚有差异,不过由于杆长的改变量 很小(在弹性范围内,£值很小),以致两杆方位的改变量很小,从而对轴力的值影响很小, 所以不必考虑。 2.在一般问题中,常根据结构变形前的原始几何情况来计算各部分的内力,在拉伸、压 缩、扭转及弯曲等问题中均可如此处理。 例2-4图2-4a所示桁架,三杆AD、BD和CD具有相同的抗拉刚度EA,试求在铅垂载荷 P作用下各杆的轴力。 D D2 (a) (b) 例图2-4 解:(1)静力平衡条件 该桁架在力P作用下,可以判断:杆AD将受拉、杆CD将受压。但杆BD在事先将难以 判断,我们可以任意假定。若假定杆BD受拉,则由节点D(图24b)的平衡条件 X=0,N:cosa-N cosa-N:=0 ① EY=0,N sina+N:sina-P=0 ② (2)变形相容条件 作节点D的位移图(图2.4c),由几何关系 -2+ tana'sina 在作位移图时应该注意,杆件的变形应与受力图中杆件的轴力相对应。也就是说,在受力 图(图24b)中已假定杆AD和BD的轴力为拉力:杆CD为压力,则在位移图(图2-4c)中, 杆AD和BD的变形应是伸长,而杆CD应是缩短
结构的变形图和节点的位移图,在计算节点位移中是等价的。在今后的计算中,可根据具 体情况,选作一图。 由位移图的几何关系,可得 水平位移 ( ) = 1 = 1 = → EA Pa x BB l A 铅垂位移 (1 2 2) ( ) 2 tan 45 2 sin 45 1 2 + = + + = = = EA Pa EA Pa EA Pa l l y A BB 要点与讨论 1.在载荷 P 作用下,由于两杆长度改变,导致节点 B 发生位移,两杆方位改变,夹角不 再为 45 ,如果按 45 求解,则两杆的轴力之值与实际数值尚有差异,不过由于杆长的改变量 很小(在弹性范围内, 值很小),以致两杆方位的改变量很小,从而对轴力的值影响很小, 所以不必考虑。 2.在一般问题中,常根据结构变形前的原始几何情况来计算各部分的内力,在拉伸、压 缩、扭转及弯曲等问题中均可如此处理。 例 2-4 图 2-4a 所示桁架,三杆 AD、BD 和 CD 具有相同的抗拉刚度 EA,试求在铅垂载荷 P 作用下各杆的轴力。 解:(1)静力平衡条件 该桁架在力 P 作用下,可以判断:杆 AD 将受拉、杆 CD 将受压。但杆 BD 在事先将难以 判断,我们可以任意假定。若假定杆 BD 受拉,则由节点 D(图 2-4b)的平衡条件 X = 0 , N3 cos − N1 cos − N2 = 0 ① Y = 0 , N1 sin + N3 sin − P = 0 ② (2)变形相容条件 作节点 D 的位移图(图 2-4c),由几何关系 tan sin 2 sin 1 2 3 l l l + = 在作位移图时应该注意,杆件的变形应与受力图中杆件的轴力相对应。也就是说,在受力 图(图 2-4b)中已假定杆 AD和 BD的轴力为拉力;杆 CD为压力,则在位移图(图 2-4c)中, 杆 AD 和 BD 的变形应是伸长,而杆 CD 应是缩短

(3)物理关系 由胡克定律 NH EA EAsin a 4= N,H EA EAtano N NH 将物理关系代入变形相容条件,整理后得补充方程 N-N:=2N2 cos2a 联立方程①②③,解得各杆轴力为 N,-N,=2sing N,=0 要点与讨论 在本题中,由于结构的对称性,在铅垂载荷P的作用下,不难判断杆BD的轴力N2=O (节点D没有水平位移)。这样,杆AD与CD的轴力N,和N,就可直接由静力平衡条件求得, 从而将问题简化为静定问题。因此,在解决实际问题时,利用结构或载荷的对称性,往往能使 解题过程大为简化。 例3-1图3-1所示传动轴,齿轮与轴用平键联接,传递转矩M=4kNm。若键的尺寸 b=24mm、h=14mm,材料的许用剪应力[女]=80MN/m2,许用挤压应力口,=100 MN/m2,试求键的长度I。 (a) (c) 解:(1)受力分析 键的受力(图3-1b) P= M 2×4×103 d/280x10-3 -100kN (2)键的长度 由剪切强度条件 所以 100×103 1e0410x网52m
(3)物理关系 由胡克定律 sin 1 1 1 1 EA N H EA N l l = = tan 2 2 2 2 EA N H EA N l l = = sin 3 3 3 3 EA N H EA N l l = = 将物理关系代入变形相容条件,整理后得补充方程 2 1 3 2 N − N = 2N cos ③ 联立方程①②③,解得各杆轴力为 2sin 1 3 P N = N = , N3 = 0 要点与讨论 在本题中,由于结构的对称性,在铅垂载荷 P 的作用下,不难判断杆 BD 的轴力 N2 = 0 (节点 D没有水平位移)。这样,杆 AD与 CD的轴力 N1 和 N3 就可直接由静力平衡条件求得, 从而将问题简化为静定问题。因此,在解决实际问题时,利用结构或载荷的对称性,往往能使 解题过程大为简化。 例 3-1 图 3-1 所示传动轴,齿轮与轴用平键联接,传递转矩 M = 4 kNm。若键的尺寸 b = 24 mm、 h =14 mm,材料的许用剪应力 = 80 NNmm2,许用挤压应力 jy = 100 NNmm2,试求键的长度 l 。 解:(1)受力分析 键的受力(图 3-1b) 100 80 10 2 4 10 2 3 3 = = = − d M P kN (2)键的长度 由剪切强度条件 = = bl P A Q 所以 ( )( ) 52 24 10 80 10 100 10 3 6 3 = = − b P l mm

由挤压强度条件 Om-Am pslon 2P 2×100×10 1产花]产04i00网x10网129m 故键的长度应取I≥143mm。在工程实际中,键为标准件,应按有关规定选用。这里可选用 平键24×12x160。 要点与讨论 1.从上述计算可见,当键的挤压应力达到其许用值时,键的工作剪应力远低于许用剪应 力。 2.一般来说,对于标准键(或花键),其挤压强度是主要矛盾,而其剪切强度一般都是足 够的,因此,在实际工作中通常仅需核算其挤压强度。对于铆钉、螺栓等联接件,其剪切强度 往往是主要的,挤压强度通常都能得到满足,因而仅需核算其剪切强度。 例3-2图3-2所示桁架支座处的榫接节点。已知水平杆为b=20cm的正方形截面,斜杆 传递的压力N=7OkN,木材的顺 纹许用拉应力[g]=l0MN/m2, 顺纹许用剪应力[]=12 MN/m?,垂直木纹方向的许用挤 压应力口n=2.5MNWm,与 为 木纹成30°角的许用挤压应力 (a) 口=5MNWm2。试求节点的 (c) 各部分尺寸h及I,和支座垫块的宽度c。 解:(1)接头尺寸 斜杆轴力N=70kN,水平杆内力S与支座反力R,汇交于点D(图3-2a),其值由节点 D(图3-2c)的平衡条件,可得 S=Ncosa,R=Nsina 由斜杆与水平杆接触面的挤压强度条件 h =Ncosa sa hh cosa 所以 h2 Ncosa_70x103cos30° 0n20x10-5x10的-6.1m 由水平杆的剪切强度条件
由挤压强度条件 jy jy jy l h P A P = = 2 则 ( )( ) 142.9 14 10 100 10 2 2 100 10 3 6 3 = = − h jy P l mm 故键的长度应取 l 143 mm。在工程实际中,键为标准件,应按有关规定选用。这里可选用 平键 2412160。 要点与讨论 1.从上述计算可见,当键的挤压应力达到其许用值时,键的工作剪应力远低于许用剪应 力。 2.一般来说,对于标准键(或花键),其挤压强度是主要矛盾,而其剪切强度一般都是足 够的,因此,在实际工作中通常仅需核算其挤压强度。对于铆钉、螺栓等联接件,其剪切强度 往往是主要的,挤压强度通常都能得到满足,因而仅需核算其剪切强度。 例 3-2 图 3-2 所示桁架支座处的榫接节点。已知水平杆为 b = 20 cm 的正方形截面,斜杆 传递的压力 N = 70 kN,木材的顺 纹许用拉应力 =10 NNmm2 , 顺 纹 许 用 剪 应 力 =1.2 NNmm2,垂直木纹方向的许用挤 压应力 2.5 90 jy = NNmm2,与 木纹成 30°角的许用挤压应力 5 30 jy = NNmm2。试求节点的 各部分尺寸 h 及 l ,和支座垫块的宽度 c 。 解:(1)接头尺寸 斜杆轴力 N = 70 kN,水平杆内力 S 与支座反力 RA 汇交于点 D (图 3-2a),其值由节点 D (图 3-2c)的平衡条件,可得 S = Ncos , RA = Nsin 由斜杆与水平杆接触面的挤压强度条件 30 cos cos jy jy bh N h b N = = 所以 ( ) ( )( ) 6.1 20 10 5 10 cos 70 10 cos30 2 6 3 30 = = − b jy N h cm 由水平杆的剪切强度条件

号" 所以 (70×103)cos30 20x1022x10网=25.3m 校核水平杆的拉伸强度 Ncosa (70x103)cos30 a-月6-价-E0x1020-6ix10=218Nm<问 故取h=7cm,1=26cm能满足强度和构造上的要求。 (2)垫块宽度 由挤压强度条件 RNsin a slo =bc bc 所以c Nsin a (70×103)sin30° 6on20x10-25x10=7cm 要点与讨论 1.木材的机械性能与作用力和木纹所夹的角度有关,也就是说,木材不是各向同性的材 料(为正交各向异性材料)。 2.有些只适用于各向同性材料的性质或关系,对于木材就不能适用。在强度计算中,应 根据受力与木纹间的夹角来选用相应的许用应力。 例41设有一实心圆轴与一内径为其二外径的空心圆轴,两轴材料及长度相同。承受转 矩均为m(例图41),已知两轴的最大剪应力相等,试比较两轴的重量。 解:设实心轴的直径为d,空心轴的外 径为D。 (1)实心轴直径d与空心轴外径D之间 的关 两轴各横截面上的扭矩相同,均为 =m 例图4-1 由最大剪应力公式,可得 实心轴 2 d 16 所以
= = bl N A Q cos30 所以 ( ) ( )( ) 25.3 20 10 1.2 10 cos 70 10 cos30 2 6 3 = = − b N l cm 校核水平杆的拉伸强度 ( ) ( ) ( ) ( )( ) 2.18 20 10 20 6.1 10 cos 70 10 cos30 2 4 3 = − = − = − = − − b h N b b h S NNmm2 故取 h = 7 cm,l = 26 cm 能满足强度和构造上的要求。 (2)垫块宽度 由挤压强度条件 90 sin jy A jy bc N bc R = = 所以 ( ) ( )( ) 7 20 10 2.5 10 sin 70 10 sin 30 2 6 3 90 = = − b jy N c cm 要点与讨论 1.木材的机械性能与作用力和木纹所夹的角度有关,也就是说,木材不是各向同性的材 料(为正交各向异性材料)。 2.有些只适用于各向同性材料的性质或关系,对于木材就不能适用。在强度计算中,应 根据受力与木纹间的夹角来选用相应的许用应力。 例 4-1 设有一实心圆轴与一内径为其 4 3 外径的空心圆轴,两轴材料及长度相同。承受转 矩均为 m (例图 4-1),已知两轴的最大剪应力相等,试比较两轴的重量。 解:设实心轴的直径为 d ,空心轴的外 径为 D 。 (1)实心轴直径 d 与空心轴外径 D 之间 的关系 两轴各横截面上的扭矩相同,均为 T = m 由最大剪应力公式,可得 实心轴 3 max 16 d T W T t = = 所以 3 max 16 d T =

空心轴 T T i064D 则 乙-无os4p Tm 由于两轴得扭矩T和最大剪应力tm分别相等,故得 24P-无o684p 所以D=1.135d (2)两轴的重量比 重量比= 04375D2_043750135d-0.564 即空心轴的重量仅为实心轴重量的56.4%。 要点与讨论 1.空心轴要较实心轴能有效地利用材料。 2.从横截面上的剪应力分布分析,由于扭转剪应力与离圆心的距离成正比,故把靠近圆 心处剪应力较小的材料移到轴的外缘处,就能充分利用材料的强度,从而节省了原材料。 3。在工程实际中,制诰空心轴是用话当外径的实心圆杆通讨钻孔加工来得到的,因此 除非在要求减轻重量为主要考虑因素的设计中(如飞机中的各种轴),或有使用要求时(如机 床主轴)采用空心轴,否则,制造空心轴并不总是值得的。 例4-2例图4-2a所示传动轴,主动轮I输入功率N,=500马力,从动轮Ⅱ、Ⅲ的输出功 率分别为N2=200马力,N,=300马力。试求(1)当AB和BC两段轴内的最大剪应力相等 时,两段轴的直径山,和d2之比和单位扭转角9,和p,之比:(2)主动轮和从动轮应如何安排 比较合理。若轴的转速n=500rm,材料的[t]=70MNm2,[o]=1°m,G=80GN/m2 并把轴设计成等截面,这时轴的直径应为多大。 解:(1)直径之比和单位扭转角之比 7024 h 024 (b) 例图4-2
空心轴 ( ) 3 4 3 max 0.684 16 4 3 1 16 D T D T W T t = − = = 则 ( ) 3 max 0.684 16 D T = 由于两轴得扭矩 T 和最大剪应力 max 分别相等,故得 ( ) 3 3 0.684 16 16 d D = 所以 D =1.135d (2)两轴的重量比 重量比 ( ) 0.564 0.4375 0.4375 1.135 4 4 3 4 2 2 2 2 2 2 2 = = = − = d d d D d D D 即空心轴的重量仅为实心轴重量的 56.4%。 要点与讨论 1.空心轴要较实心轴能有效地利用材料。 2.从横截面上的剪应力分布分析,由于扭转剪应力与离圆心的距离成正比,故把靠近圆 心处剪应力较小的材料移到轴的外缘处,就能充分利用材料的强度,从而节省了原材料。 3.在工程实际中,制造空心轴是用适当外径的实心圆杆通过钻孔加工来得到的,因此, 除非在要求减轻重量为主要考虑因素的设计中(如飞机中的各种轴),或有使用要求时(如机 床主轴)采用空心轴,否则,制造空心轴并不总是值得的。 例 4-2 例图 4-2a 所示传动轴,主动轮Ⅰ输入功率 N1 = 500 马力,从动轮Ⅱ、Ⅲ的输出功 率分别为 N2 = 200 马力, N3 = 300 马力。试求(1)当 AB 和 BC 两段轴内的最大剪应力相等 时,两段轴的直径 1 d 和 2 d 之比和单位扭转角 1 和 2 之比;(2)主动轮和从动轮应如何安排 比较合理。若轴的转速 n =500r/m ,材料的 MN/m2 = 70 , 1 /m = , 2 G = 80GN/m , 并把轴设计成等截面,这时轴的直径应为多大。 解:(1)直径之比和单位扭转角之比

所以 悟展得 由 所以 会八得 (2)传动轮合理排列,且设计成等截面时的轴径 将主动轮排在两个从动轮之间较为合理(例图42b),此时,轴的扭矩图如图42c所示 轴内的最大扭矩将较原排列时减小,为 m=m,=7024 =7024×300=4214Nm 500 设计成等截面轴时的轴径,由强度条件 16T 16×4214 d00674m 由刚度条件 32T×180 32×4214×180 d2元G阿=280×10k1 =74.5m 轴的直径应取d=74.5mm。 要点与讨论 传动轴上主动轮和从动轮安置的位置不同,轴所承受的最大扭矩也不同。 车曲,则度条件往在物 般机器的轴 件来选用轴的尺寸,再校核其是否满足刚度条件:对 例4-3一直径为8cm的安全阀,上面用平均直径 D=l60mm的弹簧压住,弹簧的预压量为 δ=30m,为保证在蒸气压力p=1.5MN/m2时开启 活塞,试求簧丝的直径和弹簧的圈数。设弹簧材料的 [t=150MN/m2,G=80GNm2。 解:(1)簧丝直径 例43 弹簧压力
由 3 2 2 3 1 1 max 16 16 d T d T W T t = = = 所以 3 3 3 1 3 2 1 2 1 3 5 = = = N N T T d d 由 4 1 1 1 1 1 32 G d T GI T p = = , 4 2 2 2 32 G d T = 所以 3 4 1 2 2 1 2 1 5 3 = = d d T T (2)传动轮合理排列,且设计成等截面时的轴径 将主动轮排在两个从动轮之间较为合理(例图 4-2b),此时,轴的扭矩图如图 4-2c 所示, 轴内的最大扭矩将较原排列时减小,为 4214 N m 500 300 max = 3 = 7024 = 7024 = n N m m 设计成等截面轴时的轴径,由强度条件 ( ) 67.4mm 70 10 16 16 4214 3 6 3 = = T d 由刚度条件 ( ) 74.5mm 80 10 1 32 180 32 4214 180 3 2 9 4 2 = = G T d 轴的直径应取 d = 74.5mm 。 要点与讨论 1.传动轴上主动轮和从动轮安置的位置不同,轴所承受的最大扭矩也不同。 2.设计一般机器的轴,常按强度条件来选用轴的尺寸,再校核其是否满足刚度条件;对 于精密机器的轴,则刚度条件往往控制设计。 例 4-3 一直径为 8cm 的安全阀,上面用平均直径 D =160mm 的弹簧压住,弹簧的预压量为 = 30mm ,为保证在蒸气压力 MN/m2 p =1.5 时开启 活塞,试求簧丝的直径和弹簧的圈数。设弹簧材料的 MN/m2 =150 , 2 G = 80GN/m 。 解:(1)簧丝直径 弹簧压力

P=p四=5x10r)8x10-=7540N 4 4 由强度条件 8PD8×7540×0.16 d≥而-50x109) =27.4mm 这时,弹簧指数 c=160 5.84 d -27.4 k-+965-126 曲度系数k并不很小,故修正设计。取d=30mm,校核强度 30=5.33 160 c= k=453-1+0615129 4×5.33-45.3 2=1298×7540x0.16=146.8MN/m2< d π×(0.03j 故取簧丝直径d=30mm是合适的。 (2)弹簧圈数 由刚度条件得 n-Gd*6.0x10k003x00-7.87 8PD 8×7540×(0.163 取n=8圈。 要点与讨论 如果要求弹簧有较好的减振和缓冲作用,即要求弹簧有较大变形和比较柔软时,应使 簧丝直径d尽可能小一些。 2.要增加入的效果,就必须增加圈数n和加大平均直径D。 例44一厚度为1,长度为1的薄板,卷成直径为D的圆筒,并承受转矩m。试求:(1) 在板边为自由的情况下(图4-4),薄壁筒的应力与扭转角:(2)在将板边焊在一起后(图4 4b),薄壁筒的应力与扭转角。 (a) 例图4-4 (b) 解:(1)开口环形薄壁杆的应力和变形 在板边为自由的情况下,可把环形展直,看作狭长矩形。于是,由矩形截面杆的扭转公式, 得最大剪应力
( ) ( ) 7540N 4 8 10 1.5 10 4 2 2 6 2 1 = = = − D P p 由强度条件 ( ) 27.4mm 150 10 8 8 7540 0.16 3 6 3 = = PD d 这时,弹簧指数 5.84 27.4 160 = = = d D c 1.26 5.84 0.615 4 5.84 4 4 5.84 1 + = − − k = 曲度系数 k 并不很小,故修正设计。取 d = 30mm ,校核强度 5.33 30 160 c = = 1.29 5.33 0.615 4 5.33 4 4 5.33 1 + = − − k = ( ) = = = 2 max 3 3 146.8MN/m 0.03 8 7540 0.16 1.29 8 d PD k 故取簧丝直径 d = 30mm 是合适的。 (2)弹簧圈数 由刚度条件得 ( ) ( ) ( ) ( ) 7.87 8 7540 0.16 80 10 0.03 0.03 8 3 4 9 4 = = = PD Gd n 取 n = 8 圈。 要点与讨论 1.如果要求弹簧有较好的减振和缓冲作用,即要求弹簧有较大变形和比较柔软时,应使 簧丝直径 d 尽可能小一些。 2.要增加 的效果,就必须增加圈数 n 和加大平均直径 D 。 例 4-4 一厚度为 t ,长度为 l 的薄板,卷成直径为 D 的圆筒,并承受转矩 m 。试求:(1) 在板边为自由的情况下(图 4-4a),薄壁筒的应力与扭转角;(2)在将板边焊在一起后(图 4- 4b),薄壁筒的应力与扭转角。 解:(1)开口环形薄壁杆的应力和变形 在板边为自由的情况下,可把环形展直,看作狭长矩形。于是,由矩形截面杆的扭转公式, 得最大剪应力