
有限元理论与建模方法 FEA&M 第十七章, 模型检查与处理 Model Checking and Processing 单元库 实际结构 设计方案 分析问题定义 几何模型建立 单元类型选择 单元特性定义 网格划分 模型检查与处理 边界条件定义 有限元模型 计算 结果比较← 模型修正
有限元理论与建模方法 FEAM Model Checking and Processing 第十七章 模型检查与处理 分 析 问 题 定 义 实际结构 有限元模型 设计方案 几 何 模 型 建 立 单 元 类 型 选 择 单 元 特 性 定 义 网 格 划 分 模 型 检 查 与 处 理 边 界 条 件 定 义 单元库 计算 结果比较 模型修正

有限元理论与建模方法 FEA&M 第一节网格质量检查 第二节重合节点检查 第三节重合与遗漏单元检查 第四节带宽优化 第五节波前处理
有限元理论与建模方法 FEAM 第三节 重合与遗漏单元检查 第一节 网格质量检查 第二节 重合节点检查 第四节 带宽优化 第五节 波前处理
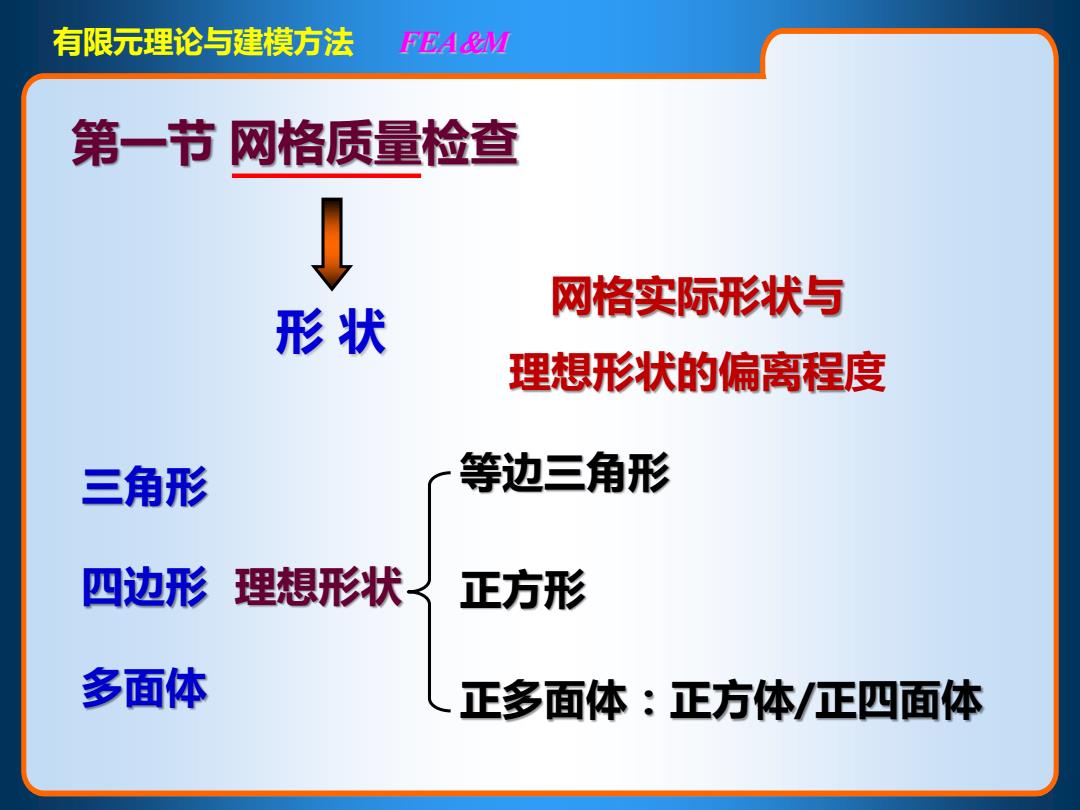
有限元理论与建模方法 FEA&M 第一节网格质量检查 网格实际形状与 形状 理想形状的偏离程度 三角形 等边三角形 四边形 理想形状〈 正方形 多面体 正多面体:正方体/正四面体
有限元理论与建模方法 FEAM 形 状 第一节 网格质量检查 理想形状 等边三角形 正方形 正多面体:正方体/正四面体 网格实际形状与 理想形状的偏离程度 三角形 四边形 多面体

有限元理论与建模方法 FEA&M 网格形状可以偏离理想形状 有限元法的优点,但有一定的“度” 越接近理想形状,质量越好。 越偏离理想形状,质量越差
有限元理论与建模方法 FEAM 网格形状可以偏离理想形状 有限元法的优点,但有一定的“度” 越接近理想形状,质量越好。 越偏离理想形状,质量越差
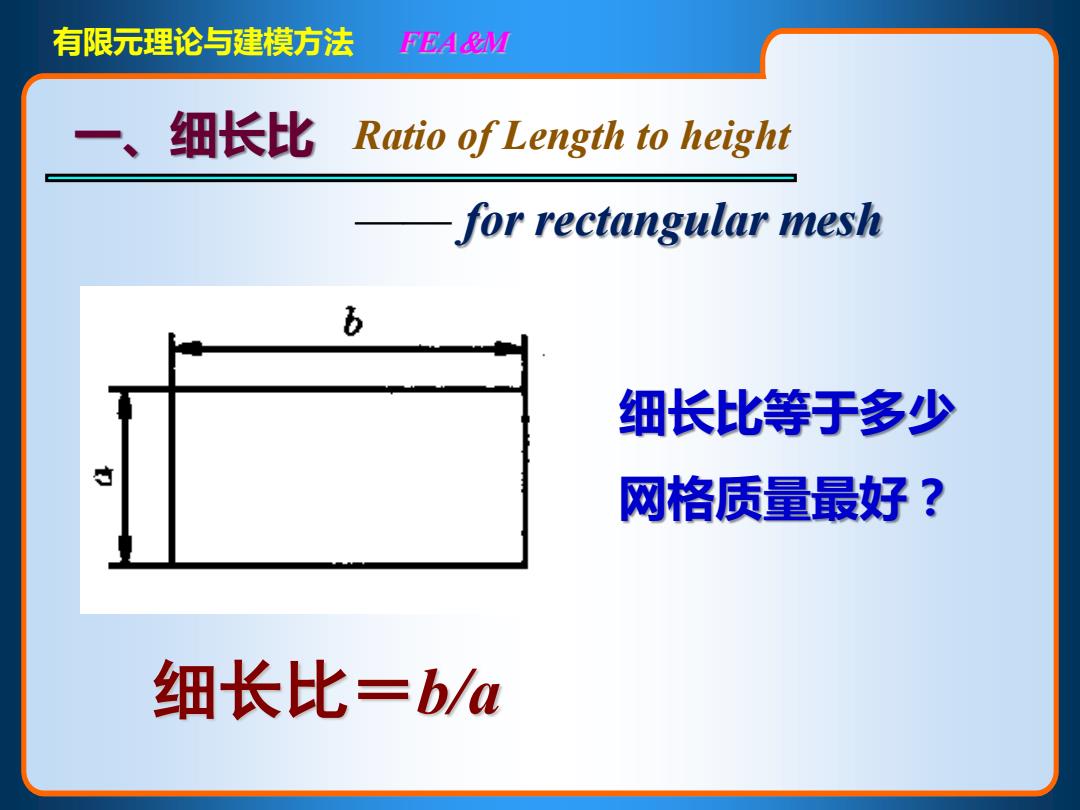
有限元理论与建模方法 FEA&M 一、 细长比Ratio of Length to height for rectangular mesh b 细长比等于多少 网格质量最好? 细长比=b/a
有限元理论与建模方法 FEAM Ratio of Length to height —— for rectangular mesh 细长比=b/a 一、细长比 细长比等于多少 网格质量最好?
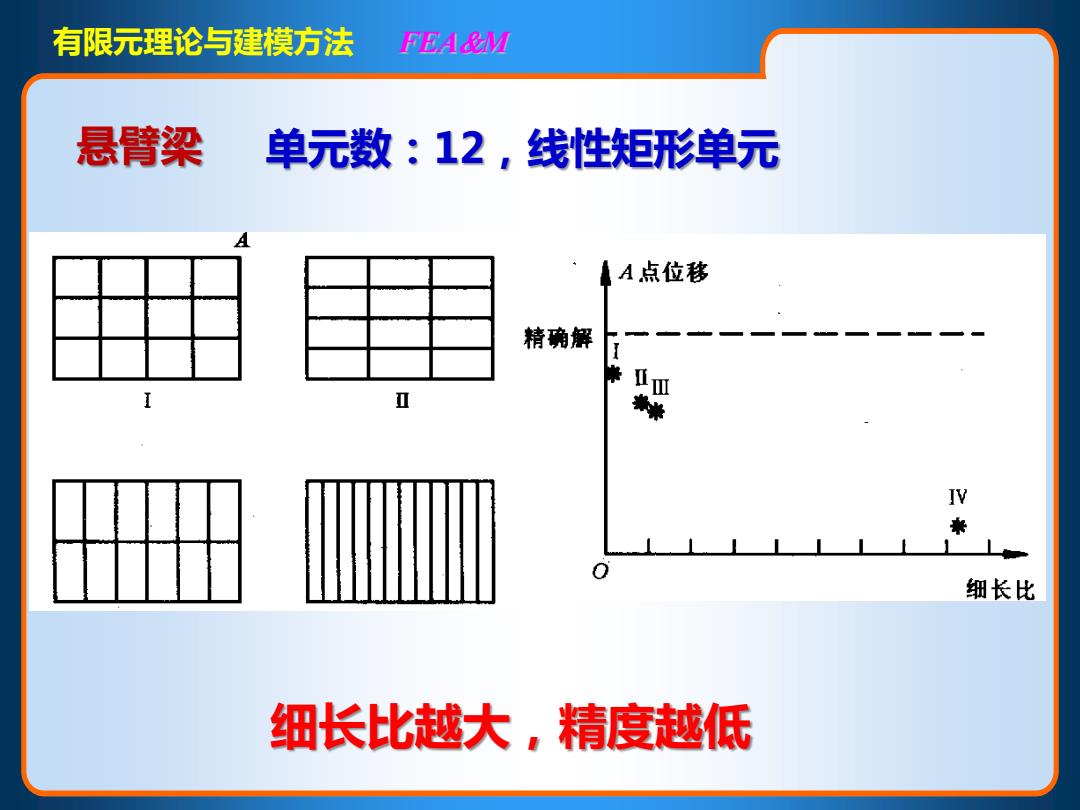
有限元理论与建模方法 FEA&M 悬臂梁 单元数:12,线性矩形单元 A点位移 精确解 I Ⅱ IV 细长比 细长比越大,精度越低
有限元理论与建模方法 FEAM 细长比越大,精度越低 悬臂梁 单元数:12,线性矩形单元
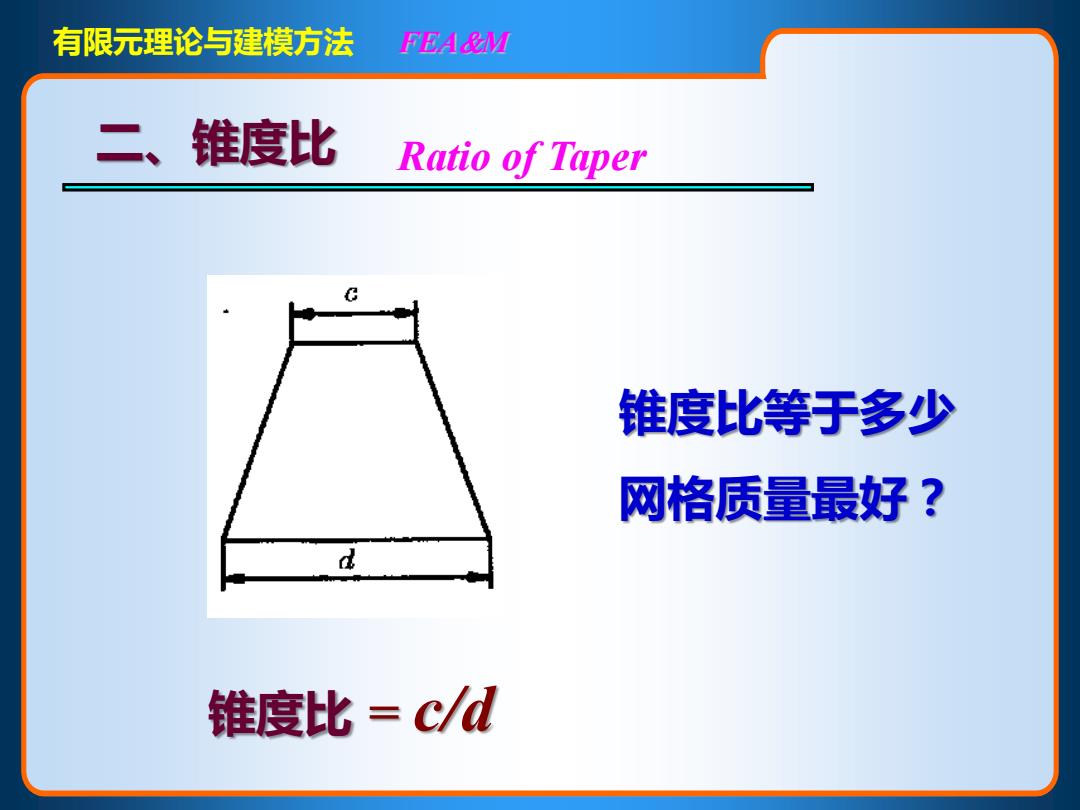
有限元理论与建模方法 FEA&M 二、锥度比 Ratio of Taper 锥度比等于多少 网格质量最好? d 锥度比=c/d
有限元理论与建模方法 FEAM Ratio of Taper 锥度比 = c/d 二、锥度比 锥度比等于多少 网格质量最好?
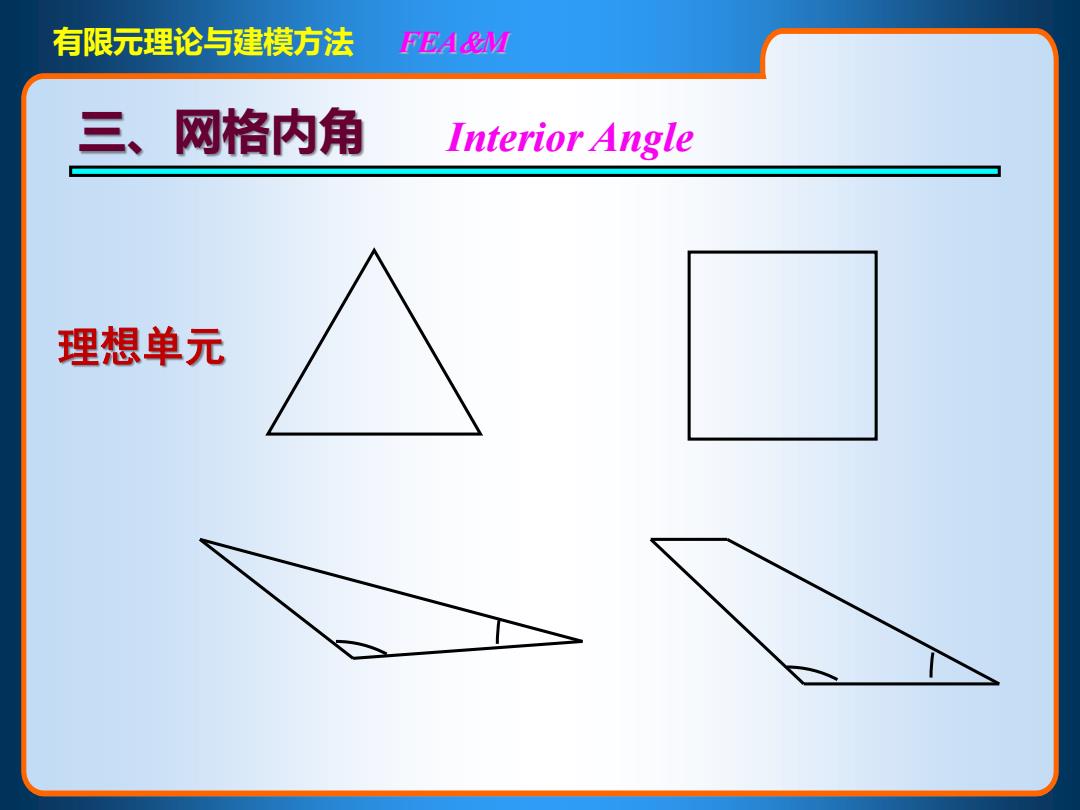
有限元理论与建模方法 FEA&M 三、网格内角 Interior Angle 理想单元
有限元理论与建模方法 FEAM 三、网格内角 Interior Angle 理想单元

有限元理论与建模方法 FEA&M 三、网格内角 Interior Angle 锥度比 顶端位移 根部应力 1.000 0.950 0.995 0.200 0.926 1.133 0.020 0.790 1.189 0.002 0.631 1.219 内角 顶端位移 根部应力 6 1.000 0.995 45 0.729 0.840 30° 0.521 0.683 150 0.282 0.270
有限元理论与建模方法 FEAM 三、网格内角 Interior Angle 60
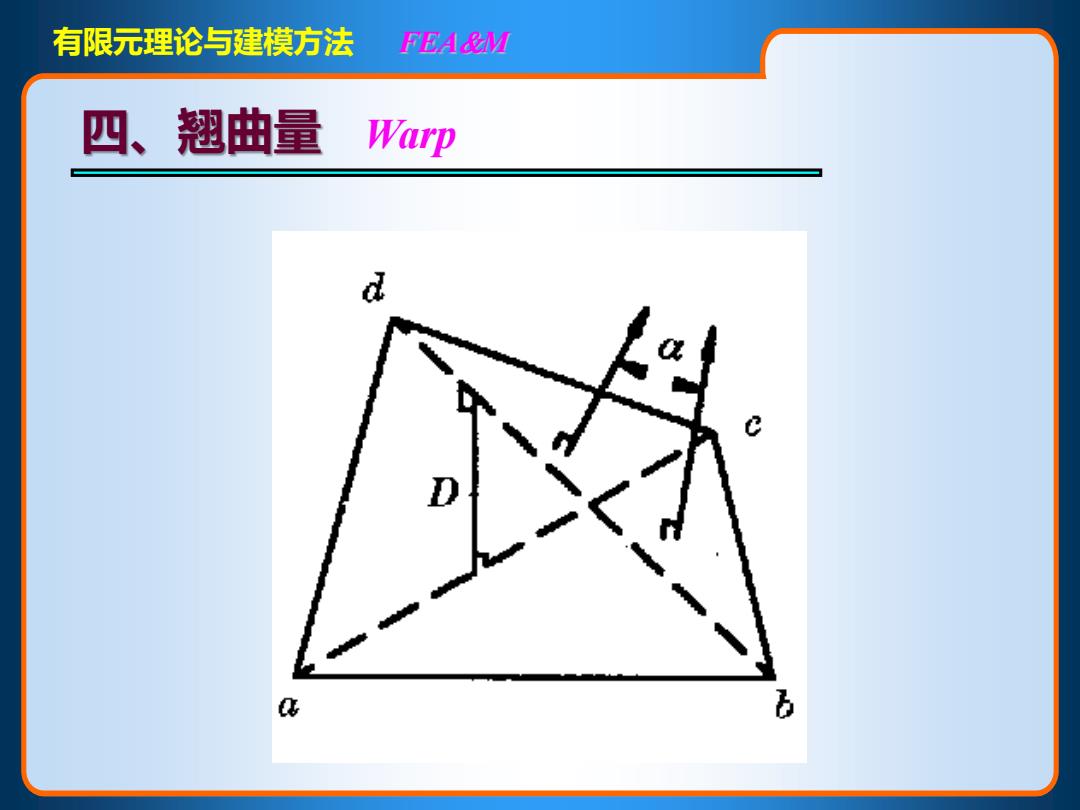
有限元理论与建模方法 FEA&M 四、翘曲量 Warp d 6
有限元理论与建模方法 FEAM 四、翘曲量 Warp