
有限元理论与建模方法 Finite Element Analysis and Modeling 第13章 有限元建模的基本原则 Basic Principles of Finite Element Modeling 保证精度原则 规模 精度 控制规模原则
有限元理论与建模方法 Finite Element Analysis and Modeling 有限元建模面临的两个问题 Basic Principles of Finite Element Modeling 第13章 有限元建模的基本原则 规 模 精 度 保 证 精 度 原 则 控 制 规 模 原 则
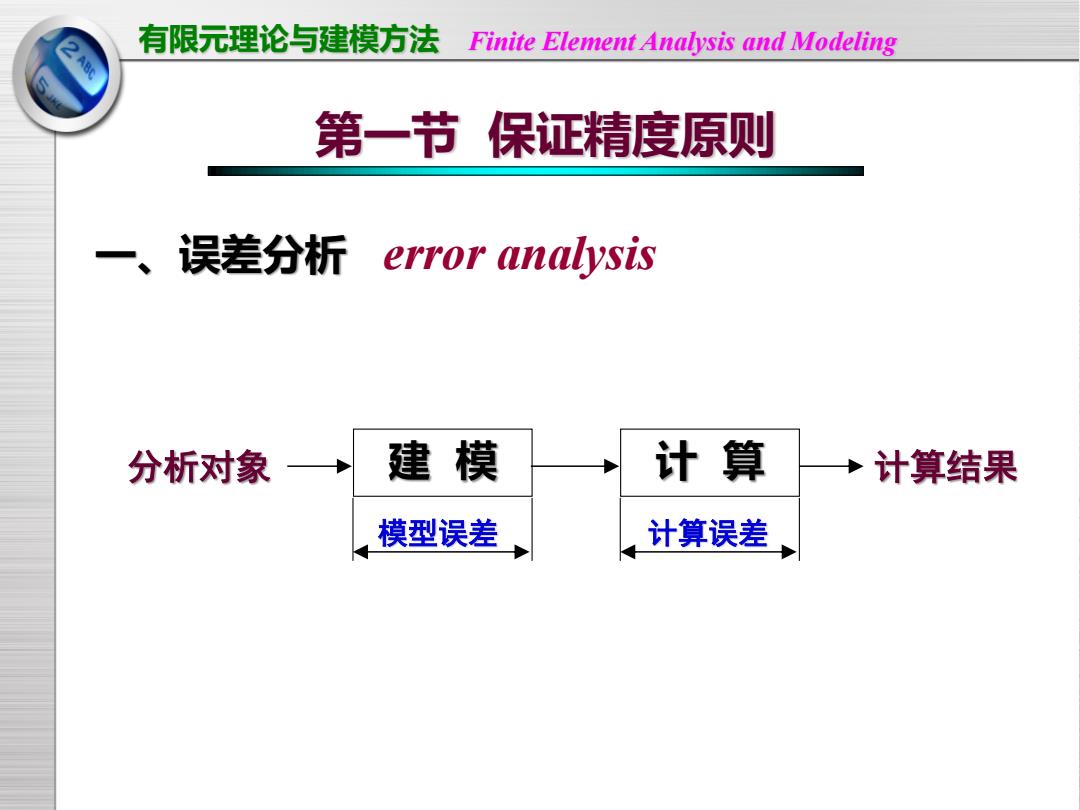
有限元理论与建模方法 Finite Element Analysis and Modeling 第一节保证精度原则 一、误差分析 error analysis 分析对象 ,+建模 计算 +计算结果 模型误差 计算误差
有限元理论与建模方法 Finite Element Analysis and Modeling 一、误差分析 模型误差 计算误差 分析对象 建 模 计 算 计算结果 第一节 保证精度原则 error analysis

有限元理论与建模方法 Finite Element Analysis and Modeling 物理离散误差 离散误差 几何离散误差 模型误差 边界条件误差 结果误差 单元形状误差 舍入误差 计算误差 截断误差 Classification of Error
有限元理论与建模方法 Finite Element Analysis and Modeling 模型误差 边界条件误差 离散误差 单元形状误差 舍入误差 截断误差 计算误差 结果误差 几何离散误差 物理离散误差 Classification of Error

有限元理论与建模方法 Finite Element Analysis and Modeling 1、模型误差 物理离散误差 原理性误差 Difference between interpolation function and actual function 如何减小物理离散误差? on function u=a+azx+a3y Unknown v=a4+a5x+av
有限元理论与建模方法 Finite Element Analysis and Modeling Difference between interpolation function and actual function u x y v x y 1 2 3 4 5 6 actual function interpolation function Unknown 物 理 离 散 误 差 1、模型误差 原理性误差 如何减小物理离散误差?

2A8 有限元理论与建模方法 Finite Element Analysis and Modeling E=O(hp+l-m h- 单元特征长度尺寸; p 单元插值多项式的最高阶次: m 函数在泛函中出现的最高阶导数。 u=1+a2x+0 u=a1+02x+43y+a4x2+0y+06y2 v=a4+asx+a6v v=a]+asx+aoy+ajox+ax+2y2 Three-node triangle: p=1,=0,O(h2) Six-node triangle: p=2,t=0,O(h3)
有限元理论与建模方法 Finite Element Analysis and Modeling ( ) p 1 m E O h Three-node triangle: p=1 , m=0 , O(h 2 ) Six-node triangle: p=2 , m=0 , O(h 3 ) h —— 单元特征长度尺寸; p —— 单元插值多项式的最高阶次; m —— 函数在泛函中出现的最高阶导数。 u x y v x y 1 2 3 4 5 6 2 1 1 1 2 2 7 8 9 1 0 2 5 6 2 1 2 3 4 v x y x xy y u x y x xy y

2 ABC 有限元理论与建模方法 Finite Element Analysis and Modeling E=O(hp+l-m) h-0 E↓ h收敛 E↓ p收敛
有限元理论与建模方法 Finite Element Analysis and Modeling h 收敛 p 收敛 h 0 E p E ( ) p 1 m E O h

有限元理论与建模方法 Finite Element Analysis and Modeling 实际位移分布 物理离散误差 单元插值函数 维单元长度 a) b】 c) h收敛 p收敛 Geometric Description
有限元理论与建模方法 Finite Element Analysis and Modeling Geometric Description h 收敛 p 收敛

2 ABC 有限元理论与建模方法 Finite Element Analysis and Modeling 几何离散误差 Difference between the shapes ≠
有限元理论与建模方法 Finite Element Analysis and Modeling —— Difference between the shapes 几何离散误差
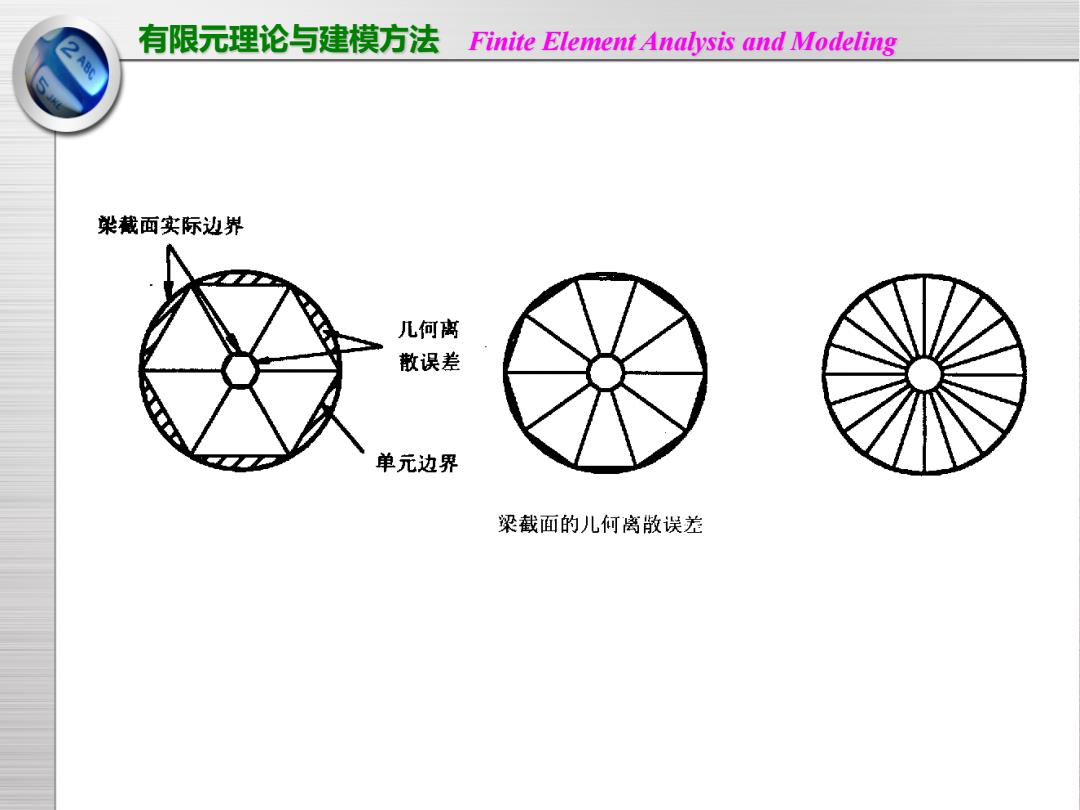
有限元理论与建模方法 Finite Element Analysis and Modeling 樂裁面实际边界 几何离 散误差 单元边界 梁截面的儿何离散误差
有限元理论与建模方法 Finite Element Analysis and Modeling

2 ABC 有限元理论与建模方法 Finite Element Analysis and Modeling 边界条件误差 Actual working 量化 Boundary condition on environment model
有限元理论与建模方法 Finite Element Analysis and Modeling Actual working environment Boundary condition on model 量 化 边界条件误差