
第二章有限元法的基本原理 平面问题有限元法 第一节弹性力学有关知识 位移场 应力场 第二节平面问题有限元法 6学时 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 第二章 有限元法的基本原理 第一节 弹性力学有关知识 第二节 平面问题有限元法 —— 平面问题有限元法 6学时 位移场 应力场

Review 数值计算方法 近似解 微分方程边值问题 差分法、变分法 离散、分片插值 非均匀网格:适应性,精度 简化插值函数 单元、节点 单元通过节点连接 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 数值计算方法 近似解 差分法、变分法 微分方程边值问题 离散、分片插值 单元、节点 非均匀网格:适应性,精度 简化插值函数 Review 单元通过节点连接

基本思路 物理问题 弹性力学: 平衡、几何、物理方程 0 传热学: 控制方程 微分方程 热传导微分方程 流体力学: 离散、分片插值 质量、动量、能量守恒方程 有限元方程 代数方程 电磁学: 麦克斯韦方程 数值算法 数值求解 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 基本思路 控制方程 物理问题 弹性力学: 平衡、几何、物理方程 传 热 学: 热传导微分方程 流体力学: 质量、动量、能量守恒方程 电 磁 学: 麦克斯韦方程 微分方程 有限元方程 代数方程 离散、分片插值 数值求解 数值算法

第一节弹性力学有关知识 一、弹性力学中的基本物理量 与材料力学相同 空间结构(块体) 杆件结构 薄壁结构(薄板/薄壳) 载荷(Ioad) 研究对象不同 ◆应力(Stress) 研究内容相同 应变(Strain) ◆位移(Displacement) 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 第一节 弹性力学有关知识 载荷 (load) 应力 (Stress) 应变 (Strain) 位移 (Displacement) 一、弹性力学中的基本物理量 与材料力学相同 空间结构(块体) 杆件结构 薄壁结构(薄板/薄壳) 研究对象不同 研究内容相同

载荷 网 外界作用在弹性体上的力,又称为外力 Concentrated force load Surface force Volume force 转置 PPer Poy Pe Ps)=Psx Psy Ps Pypw Pw pr 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 load Concentrated force Surface force Volume force {P v }={pvx pvy pvz } T {P c }={ pcx pcy pcz } T {P s }={ psx psy psz } T 外界作用在弹性体上的力,又称为外力 载 荷 转置
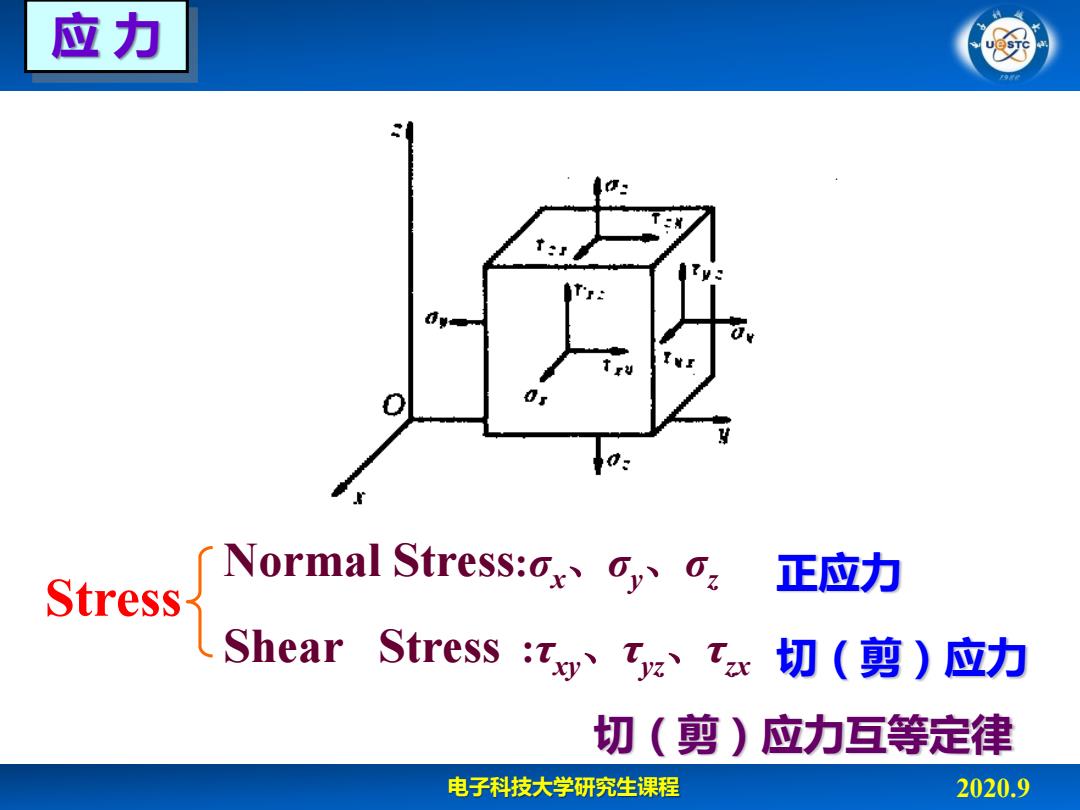
应力 呀 Normal Stress:ox. 正应力 Stress Shear Stress :tyyat 切(剪)应力 切(剪)应力互等定律 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 Stress Normal Stress:σx、σy、σz Shear Stress :τxy、τyz、τzx 应 力 正应力 切(剪)应力 切(剪)应力互等定律

例 6个独立应力分量 {o}={0x0y 0 T T XV YZ 应力状态 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 {σ}={σ x σ y σ z τ xy τ yz τ zx } T 6个独立应力分量 应力状态

应变 咧 d d. Normal Strain:xy 82 ← 正应力 Strain Shear Strain:"g、"z'x←t切应力 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 Strain Normal Strain: εx、εy、εz Shear Strain : νxy 、νyz 、νzx 应 变 dz ydy dz yz O dy dy dx dx O y y z z x x 正应力 切应力
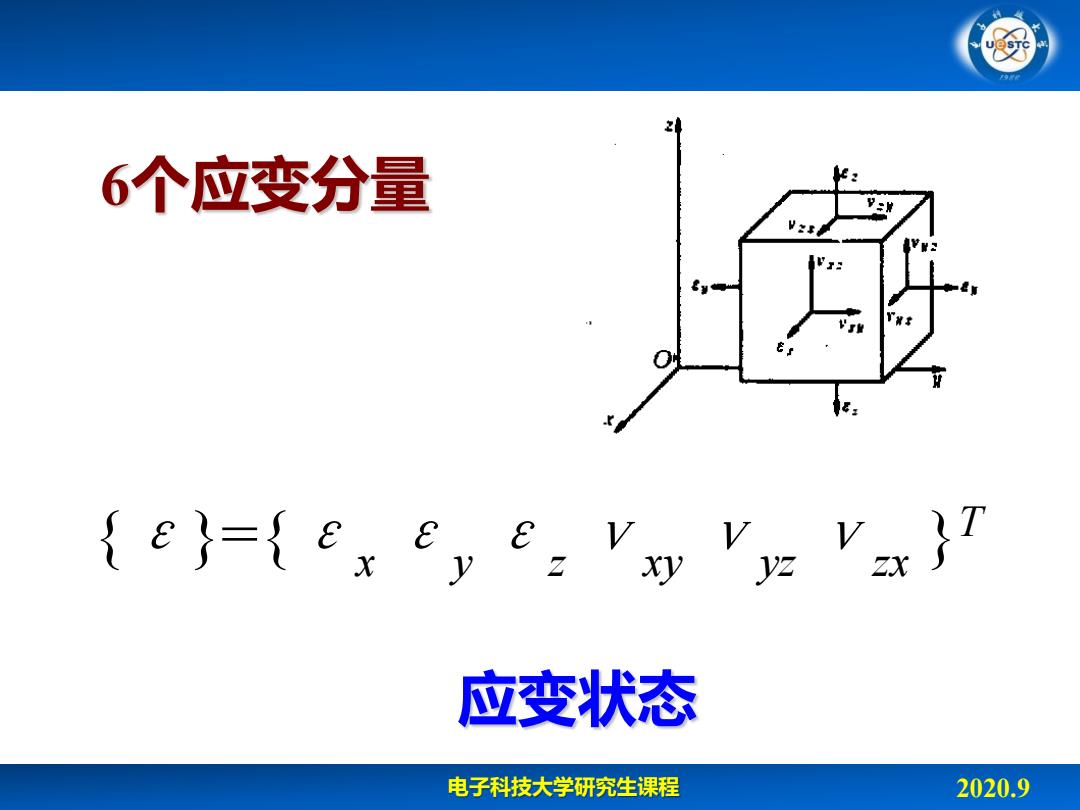
呀 6个应变分量 k e3={ex ex E E V xy z x}7 应变状态 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 {ε}={ε x ε y ε z ν xy ν yz ν zx } T 6个应变分量 应变状态

位移 呀 弹性体内质点位置的移动 x axis:/u Displaeceneat y axis;v z axis: {d;=fu v wyr 所有质点的位移—— 位移场 变形(deform,deformation) 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 Displacement x axis: u y axis: v z axis: w {d}={u v w} T 位 移 变形(deform,deformation) 弹性体内质点位置的移动 所有质点的位移——位移场