
第一章绪论 第一节有限元法的产生与基本思想 第二节有限元法的应用 第三节有限元法在产品开发中的作用 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 第一节 有限元法的产生与基本思想 第一章 绪 论 第二节 有限元法的应用 第三节 有限元法在产品开发中的作用
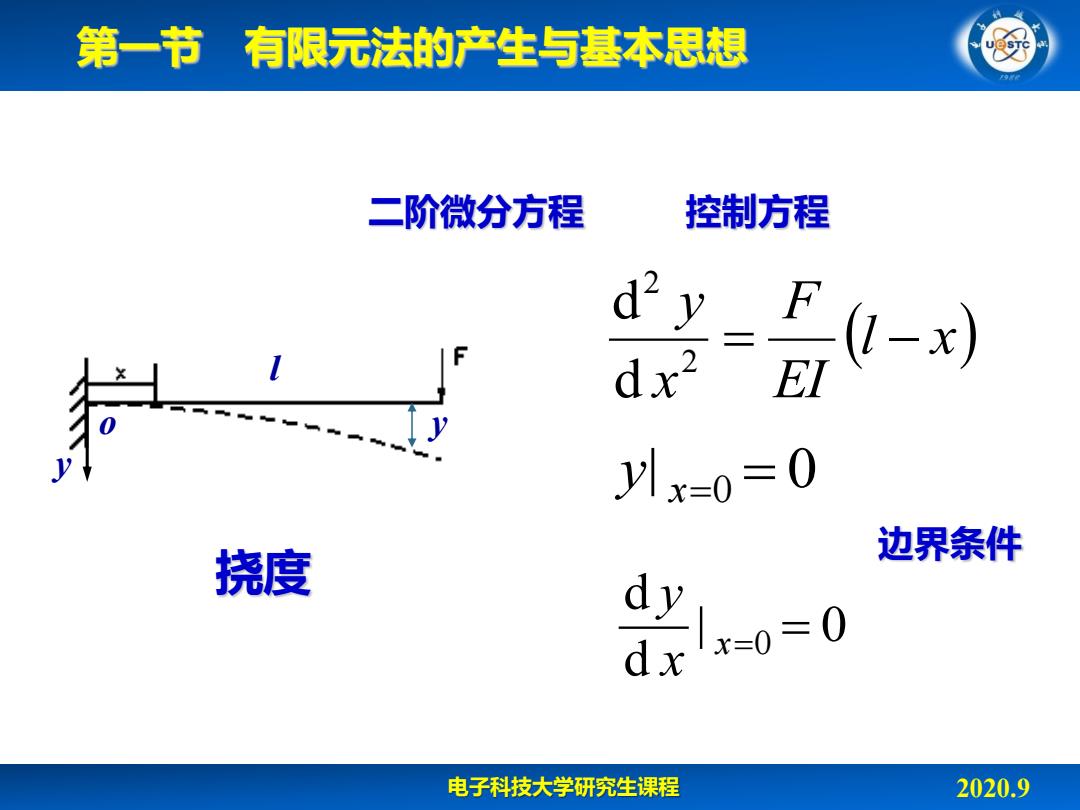
第一节有限元法的产生与基本思想 呀 二阶微分方程 控制方程 d2 dx2 - y y川x=0=0 边界条件 挠度 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 l x EI F x y 2 2 d d y x0 0 d d y x x0 0 第一节 有限元法的产生与基本思想 o y l y 挠度 二阶微分方程 控制方程 边界条件

呀 热传导微分方程 ∂2T 62T X =0 &2 22 温度分布 +a1.0 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 0 2 2 2 2 2 2 z T y T x T 0 T Tm n T Tm 温度分布 热传导微分方程

例 微分方程 (differential equation) 微分方程边值问题 边界条件 (boundary condition) 微分方程 (differential equation) 微分方程初值问题 初始条件 (initial condition) 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 微分方程 (differential equation) 边界条件 (boundary condition) 微分方程边值问题 微分方程初值问题 微分方程 (differential equation) 初始条件 (initial condition)

d2y dx2 0-x) EI y川x=0=0 1=0 Mathematical Mathematical model modeling Physical Mathematical problem problem F x3 y= 10= (Lx- max 3EI solve 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 Physical problem Mathematical problem Mathematical model solve Mathematical modeling ` l x EI F x y 2 2 d d y x0 0 d d y x x0 0 ` 2 6 2 3 lx x EI F y 3 max 3 Fl y EI ) 2 ( 2 x lx EI F
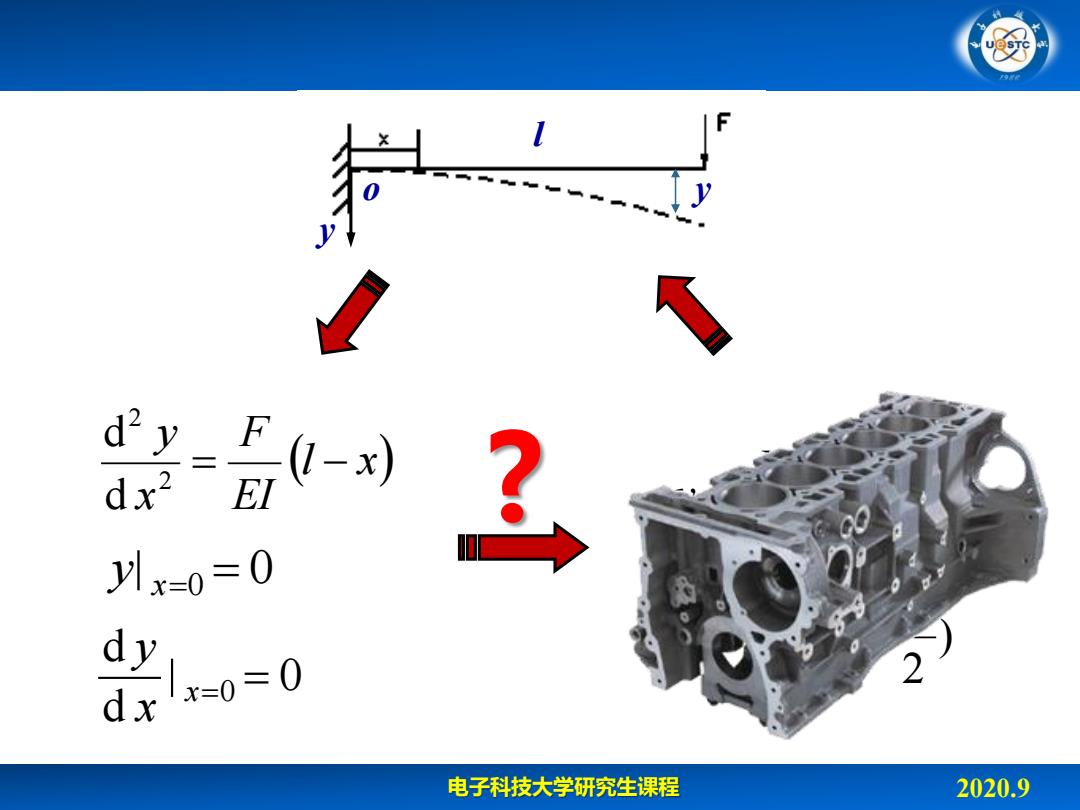
例 。 1 d2y 、 dx2 3 yx=0 =0 y 2 x=0=0 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 l x EI F x y 2 2 d d y x0 0 d d y x x0 0 o y l y ) 2 6 ( 2 3 lx x EI F y ) 2 ( 2 x lx EI F ?

严格的数学推导; 精确的解的表达式 唯一的 Analytical method解析方法 F Solve methody= EI Numerical method数值方法 利用数值算法 在计算机上 有限元法 计算近似解 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 Solve method Analytical method 解析方法 Numerical method 数值方法 有限元法 ) 2 6 ( 2 3 lx x EI F y ) 2 ( 2 x lx EI F 利用数值算法 在计算机上 计算近似解 严格的数学推导 精确的解的表达式 唯一的

阿 有限元法的来源? 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 有限元法的来源?
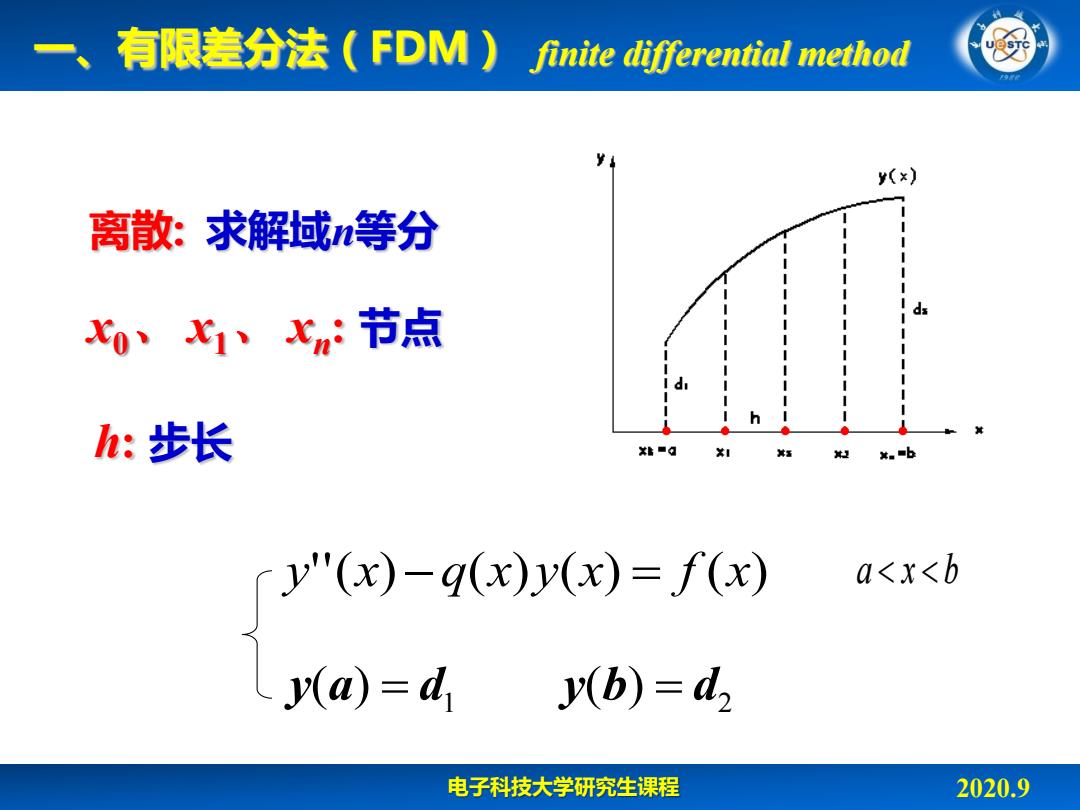
一、有限差分法(FDM)finite differential method y(x) 离散:求解域等分 X0、X1、心n:节点 h:步长 t■q 。■ y"'(x)-q(x)y(x)=f(x) a<x<b y(a)=d y(b)=d 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 finite differential method y''(x) q(x)y(x) f (x) a x b 1 2 y(a) d y(b) d 一、有限差分法(FDM) 离散: h: 步长 x0、 x1、 xn : 节点 求解域n等分
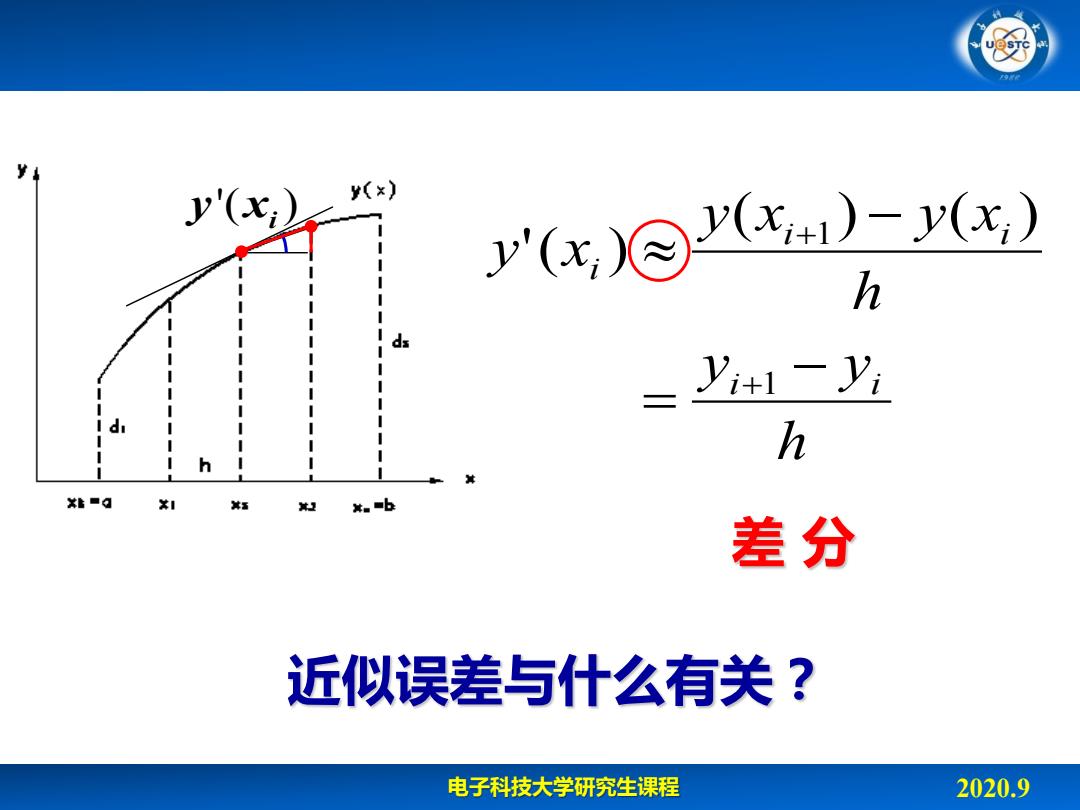
y'(x:) (x) ()-(x) h yi+y I d h h 其 X6■q 其五 #。■b 差分 近似误差与什么有关? 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 差 分 h y y h y x y x y x i i i i i 1 1 ( ) ( ) '( ) '( )i y x 近似误差与什么有关?