
第四节事故预测与预防 一、事故预测方法 ·预测--是指预测者根据有关的历史资料和现实资料,运用 适当的方法和技巧,对研究对象的未来状态进行科学的分析、 估算和推断,并对预测结果进行验证评价和应用的活动过程。 ·事故预测--也称为安全性预测,是对系统将来的安全状况 进行的预测。伤亡事故预测包括事故发生可能性预测和事故 发生趋势预测 ·常用的伤亡事故发生预测方法 。回归预测法、指数平滑法、灰色系统预测法、卡尔曼滤波器预 测法等。在此只介绍灰色系统预测法
◼ 一、事故预测方法 ◼ 预测----是指预测者根据有关的历史资料和现实资料,运用 适当的方法和技巧,对研究对象的未来状态进行科学的分析、 估算和推断,并对预测结果进行验证评价和应用的活动过程。 ◼ 事故预测----也称为安全性预测,是对系统将来的安全状况 进行的预测。伤亡事故预测包括事故发生可能性预测和事故 发生趋势预测 ◼ 常用的伤亡事故发生预测方法 ◼ 回归预测法、指数平滑法、灰色系统预测法、卡尔曼滤波器预 测法等。在此只介绍灰色系统预测法。 第四节 事故预测与预防

灰色系统预测法 创建 。 灰色系统理论邓聚龙教授在1982年创立的,它以“部分信息已知,部 分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象,要 通过对“部分”已知信息的生成、开发,提取有价值的信息,实现对系 统运行规律的正确认识和确切描述,并据以进行科学预测。 ■定义 ·把内部信息已知的系统称为白色系统;信息未知的或非确知的系统称为 黑色系统;而把信息不完全确知的系统称为灰色系统。 ·灰色系统的基本特征是构成系统的因素有些是清楚的,而另一些则不太 清楚,于是系统既不“白”也不“黑”,呈“灰色”。 ·应用 。有些事故致因因素及其对事故发生的作用很清楚,有些则不清楚。因此, 可以借助灰色系统理论来研究
◼ 创建 ◼ 灰色系统理论邓聚龙教授在1982年创立的,它以“部分信息已知,部 分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象,要 通过对“部分”已知信息的生成、开发,提取有价值的信息,实现对系 统运行规律的正确认识和确切描述,并据以进行科学预测。 ◼ 定义 ◼ 把内部信息已知的系统称为白色系统;信息未知的或非确知的系统称为 黑色系统;而把信息不完全确知的系统称为灰色系统。 ◼ 灰色系统的基本特征是构成系统的因素有些是清楚的,而另一些则不太 清楚,于是系统既不“白”也不“黑” ,呈“灰色”。 ◼ 应用 ◼ 有些事故致因因素及其对事故发生的作用很清楚,有些则不清楚。因此, 可以借助灰色系统理论来研究。 灰色系统预测法

数据生成 灰色系统的一个基本观点是把一切随机变量都看作是在一定范 围内变化的灰色量。根据灰色系统理论,处理灰色量不是采用 通常的数理统计方法,而是采用数据生成的方法来寻求其中的 规律性。灰色系统数据生成方式有三种: (1)累加生成。通过数据列中各数据依次累加得到新的数据列。 累加前的数据列称为原数据列,累加后生成的数据列称为生成 数据列。 (2)累减生成。通过数据列中各数据相减得到新的数据列。累 减是累加的逆运算。 (3)映射生成。除了累加和累加、累减之外的其他生成
◼ 灰色系统的一个基本观点是把一切随机变量都看作是在一定范 围内变化的灰色量。根据灰色系统理论,处理灰色量不是采用 通常的数理统计方法,而是采用数据生成的方法来寻求其中的 规律性。灰色系统数据生成方式有三种: (1)累加生成。通过数据列中各数据依次累加得到新的数据列。 累加前的数据列称为原数据列,累加后生成的数据列称为生成 数据列。 (2)累减生成。通过数据列中各数据相减得到新的数据列。累 减是累加的逆运算。 (3)映射生成。除了累加和累加、累减之外的其他生成。 1.数据生成

在伤亡事故发生趋势预测中主要采用累加生成的 方式进行数据处理。 设有原始数据列XO x0=(k0kk=12,3,n x( =(xo(),xo(2),xo3),,xon) 显然,生成数据列与原始数据列之间有如下关系: x0)=∑x间 i-1 经过累加生成得到的生成数据列比原始数据列的 随机波动性减弱了,内在的规律性显现出来了
在伤亡事故发生趋势预测中主要采用累加生成的 方式进行数据处理。 设有原始数据列 (0) x ( ) ( ) x (x (k)k 1,2,3,...,n) 0 0 = = ( ) ( ) ( ) ( ) ( ) ( ) ( ) (x 1 , x 2 , x 3 ,...,x (n)) 0 0 0 0 = 显然,生成数据列与原始数据列之间有如下关系: (1) x (0) x ( ) ( ) ( ) ( ) = = k i 1 1 0 x k x i 经过累加生成得到的生成数据列比原始数据列的 随机波动性减弱了,内在的规律性显现出来了

2.建立灰色模型 对于生成数据列x可以建立白化形式的微分方程, 它称为一阶灰色微分方程记为 GM,即一阶一个 变量的微分方程: dx( +ax()=u dt 其中a和u是待定参数。 该方程的解为: k+)-(0-8e+日 该式称为时间反应方程。记参数列为a a 或a=(a,u)r 可以利用最小二乘法求解a:a=(BTB尸BTyN
对于生成数据列 可以建立白化形式的微分方程, 它称为一阶灰色微分方程记为 , 即一阶一个 变量的微分方程: GM(1,1) ( ) ( ) ax u dt dx 1 1 + = 其中 a 和 u 是待定参数。 该方程的解为: ( ) ( ) ( ) ( ) a u e a u xˆ k 1 x 1 1 1 ak + + = − − 该式称为时间反应方程。记参数列为 ( ) N T 1 T a ˆ B B B y − = = u a aˆ ( ) T 或 a ˆ = a,u 可以利用最小二乘法求解 a ˆ : a ˆ 2.建立灰色模型 (1) x

其中, 号(k@)+x0(2) B= -,(02)+x0B) 1 -ka-+xoa》1 yN=(x0(2),x(3),,xon
( ) ( ) ( ) ( ( )) ( ) ( ) ( ) ( ( )) ( ) ( ) ( ) ( ( )) − − + − + − + = x n 1 x n 1 2 1 ... ... x 2 x 3 1 2 1 x 1 x 2 1 2 1 B 1 1 1 1 1 1 其中, ( ) ( ) ( ) ( ) ( ) ( ( )) T 0 0 0 y N = x 2 , x 3 ,..., x n

3.后验差检验 为检验按灰色模型预测的可信性,需要进行后验差检验。 原始数据列的实际数据的平均值x和方差S,分别为: x=2x6) n s2-2k)-刘 1.1 把第k项数据的原始数据值xO(k)与计算的估计值o(k)之差q) 称作第K项残差 q(k)=x(k)-(k) 则整个数据列所有数据项的残差的平均值和方差S,分别为: -}2a)s,-2a个-动
3.后验差检验 为检验按灰色模型预测的可信性,需要进行后验差检验。 原始数据列的实际数据的平均值 x 和方差 分别为: 2 S1 ( ) ( ( ) ) 2 n k 1 2 0 1 x k x n 1 S = = − ( ) ( ) = = n k 1 0 x k n 1 x 把第 项数据的原始数据值 与计算的估计值 之差 称作第K项残差 k ( ) x (k) 0 ( ) x ˆ (k) 0 q(k) ( ) ( ) ( ) ( ) q k x k x ˆ (k) 0 0 = − 则整个数据列所有数据项的残差的平均值 和方差 分别为: 2 q S2 ( ) = = n k 1 q k n 1 q ( ( ) ) 2 n k 1 2 2 q k q n 1 S = = −

通过计算后验差比值C和小误差频率P来进行 后验差检验。 (1)后验差比值。按定义,后验差比值为 C= S 后验差比值C越小越好。C小则意味着$小而$2大,即尽管原 始数据很离散,按灰色模型计算的估计值与实际值很接近。 (2)小误差频率。按定义,小误差频率为残差与残差平均值 之差小于给定0.6745S的频率: P=Pqk)-可<0.6745S} 小误差频率越大越好。 根据后验差比值和小误差频率可以综合评价模型的精度,见表15-3
通过计算后验差比值 和小误差频率 来进行 后验差检验。 (1)后验差比值。按定义,后验差比值为 1 2 S S C = 后验差比值 越小越好。 小则意味着 小而 大,即尽管原 始数据很离散,按灰色模型计算的估计值与实际值很接近。 C S1 S2 (2)小误差频率。按定义,小误差频率为残差与残差平均值 之差小于给定值 6745S 的频率: 1 0. P = Pq(k)− q 0.6745S1 小误差频率越大越好。 根据后验差比值和小误差频率可以综合评价模型的精度,见表15-3。 C P C C
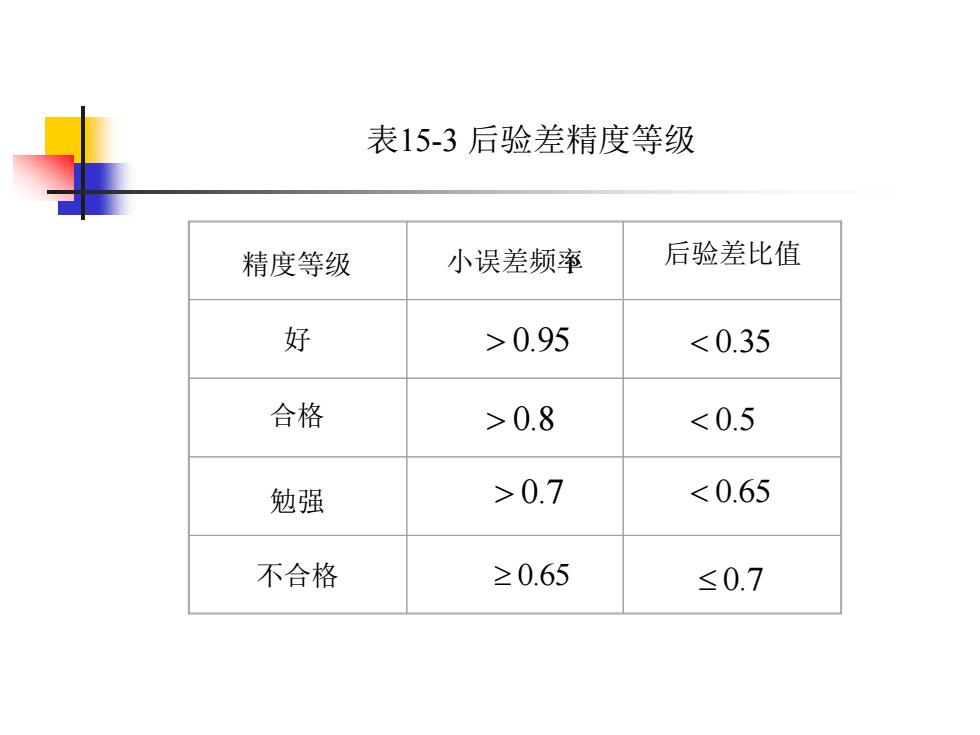
表15-3后验差精度等级 精度等级 小误差频率 后验差比值 好 >0.95 0.8 0.7 <0.65 不合格 ≥0.65 ≤0.7
表15-3 后验差精度等级 P 0.95 0.35 0.8 0.5 0.7 0.65 0.65 0.7 精度等级 小误差频率 后验差比值 好 合格 勉强 不合格

4.7 残差模型 如果经过后验差检验根据原始数据列建立的灰色模型不合格, 可以建立残差模型对原模型修正。 对累加生成的数据列的数据顼计算残差: q0(k)=x0(k)-0(k) 组成残差数据列g四 g0=q00,g0(2),g03).…,g06n》 一般只用部分残差而不是全部残差建立残差模型,即m<n。 将残差数据列进行累加生成得到残差累加生成数据列,建立一阶 微分方程: +ag0=4 dt 该方程的解为: 9e+-g0-受et-e 0①)=g0①
4.残差模型 如果经过后验差检验根据原始数据列建立的灰色模型不合格, 可以建立残差模型对原模型修正。 对累加生成的数据列的数据项计算残差: ( ) ( ) ( ) ( ) ( ) q k x k x ˆ (k) 1 1 1 = − 组成残差数据列 (1) q ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ( )) 1 1 1 1 1 1 q = q 1 ,q 2 ,q 3 ,...,q n 一般只用部分残差而不是全部残差建立残差模型,即 n1 n 。 将残差数据列进行累加生成得到残差累加生成数据列,建立一阶 微分方程: ( ) ( ) 1 1 1 1 a q u dt dq + = 该方程的解为: ( ) ( ) ( ) ( ) ( ) ( ) a k a k e e a u q k q 1 1 1 1 1 1 1 ˆ 1 1 − + − − + = − ( ) ( ) ( ) ˆ 1 (1) 1 1 q = q