
第六章投影变换 6-01 6-09 6-15解法三 6-20 6-28 6-02○ 6-10● 6-15解法 46-21D 6-29》 6-03 6-11 6-15解法四 @6-22 6-30 6-04 6-12解法→ 6-16 6-23 6-05● 6-12解法三 6-17 6-24 6-06 6-13 6-18解法→→ e6-25D 6-07 6-14 6-18解法三 6-26 6-08 6-15解法→ 6-19 6-27 阿
第六章 投影变换 6-13 6-14 6-12解法二 6-10 6-11 6-09 6-16 6-17 6-28 6-06 6-07 6-08 6-05 6-02 6-03 6-04 6-01 6-25 6-26 6-19 6-24 6-21 6-22 6-23 6-20 6-29 6-30 6-12解法一 6-15解法三 6-15解法二 6-15解法一 6-18解法二 6-15解法四 6-18解法一 6-27 退出
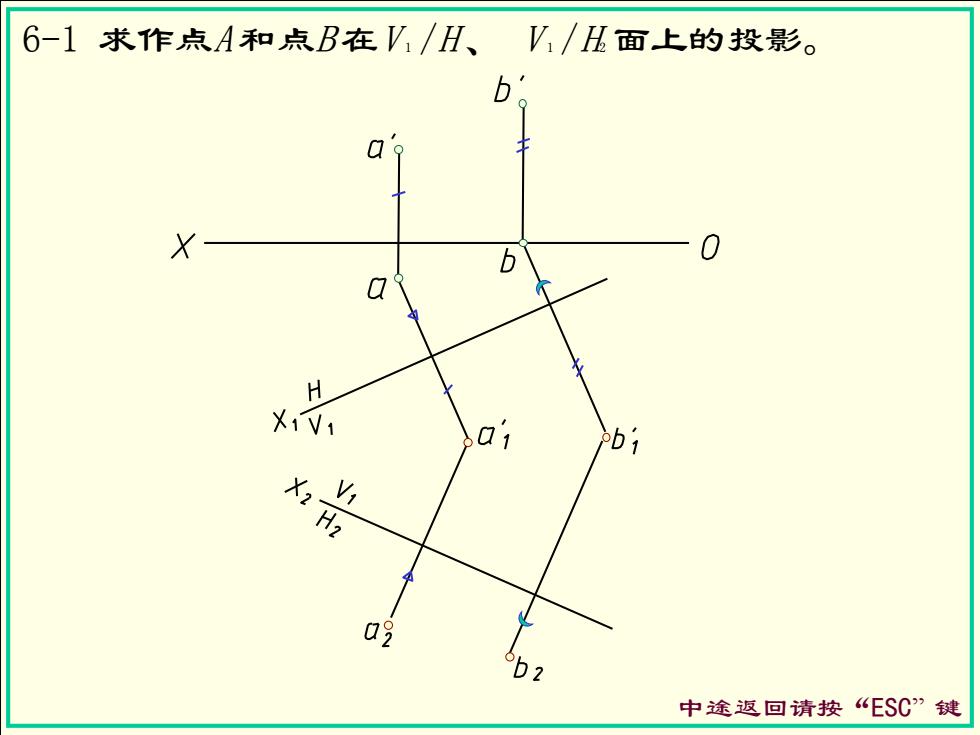
6-1求作点A和点B在V1/H、V/B面上的投影。 b X b H XiV 01 b1 X2 02 6b2 中途返回请按“ESC”键
6-1 求作点A 和点B 在V 1 /H 、 V 1 /H2 面上的投影。 中途返回请按“ESC” 键
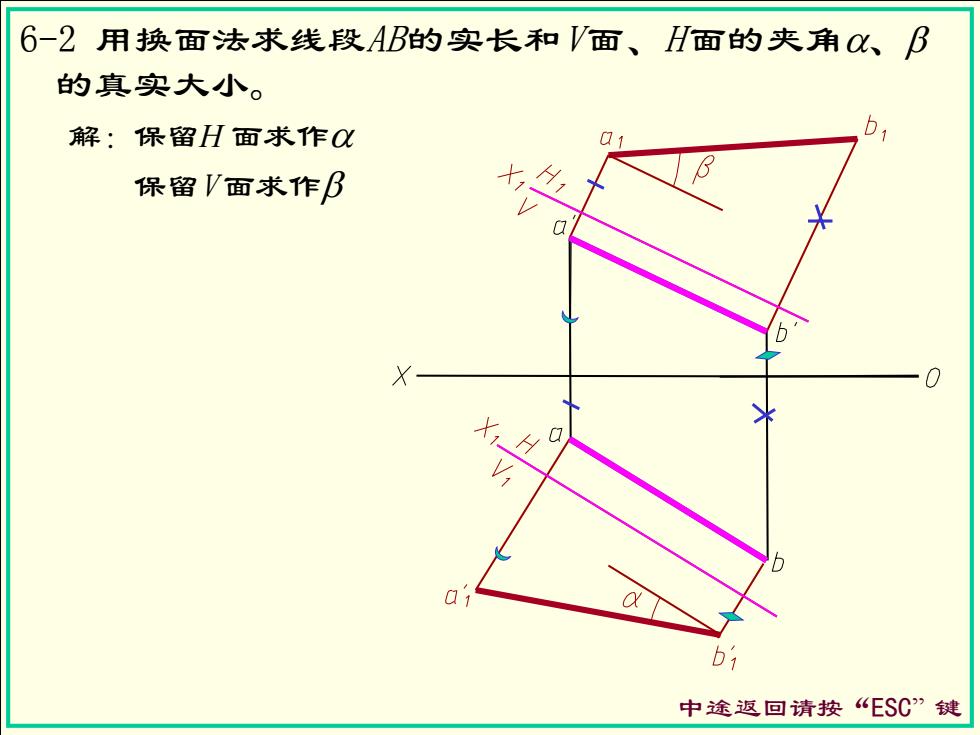
6-2用换面法求线段AB的实长和V面、H面的夹角、B 的真实大小。 解:保留H面求作0 保留V面求作B X <I 0 x bi 中途返回请按“ESC”键
6-2 用换面法求线段AB的实长和V面、H面的夹角a、b 的真实大小。 中途返回请按“ESC” 键 保留V 面求作b 解:保留H 面求作a
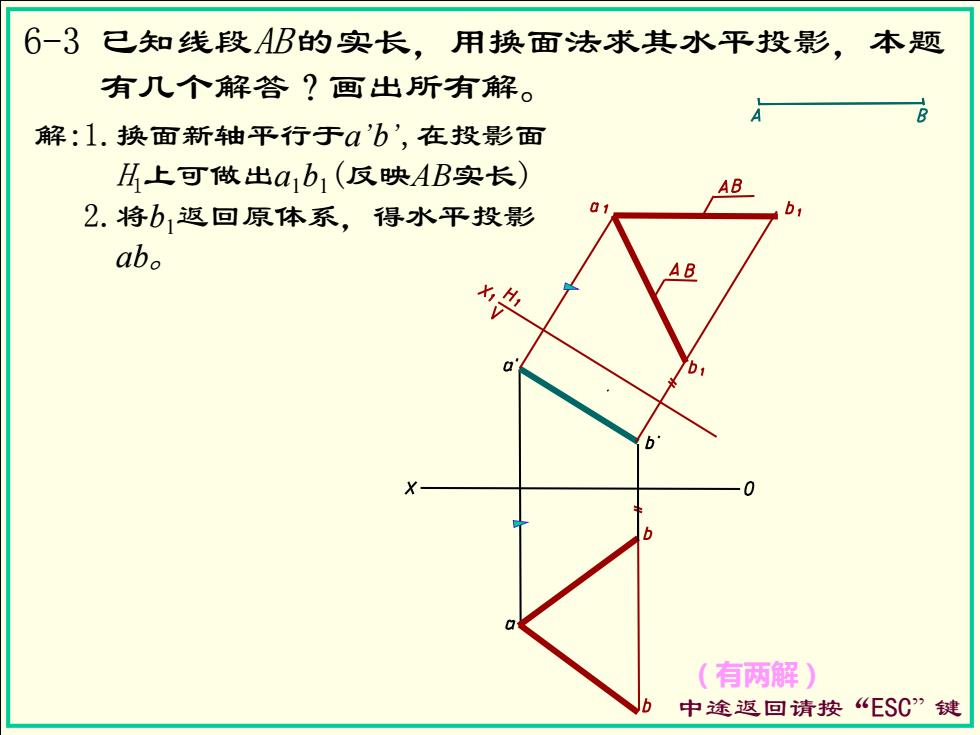
6-3已知线段AB的实长,用换面法求其水平投影,: 本题 有几个解答?画出所有解。 解:1.换面新轴平行于a'b',在投影面 以上可做出☑1b1(反映AB实长) AB 2.将b,返回原体系,得水平投影 abo AB (有两解) 中途返回请按“ESC”键
(有两解) 6-3 已知线段AB 的实长,用换面法求其水平投影,本题 有几个解答?画出所有解。 中途返回请按“ESC” 键 解:1.换面新轴平行于a’b’,在投影面 H1上可做出a1b1(反映AB实长) 2.将b1返回原体系,得水平投影 ab
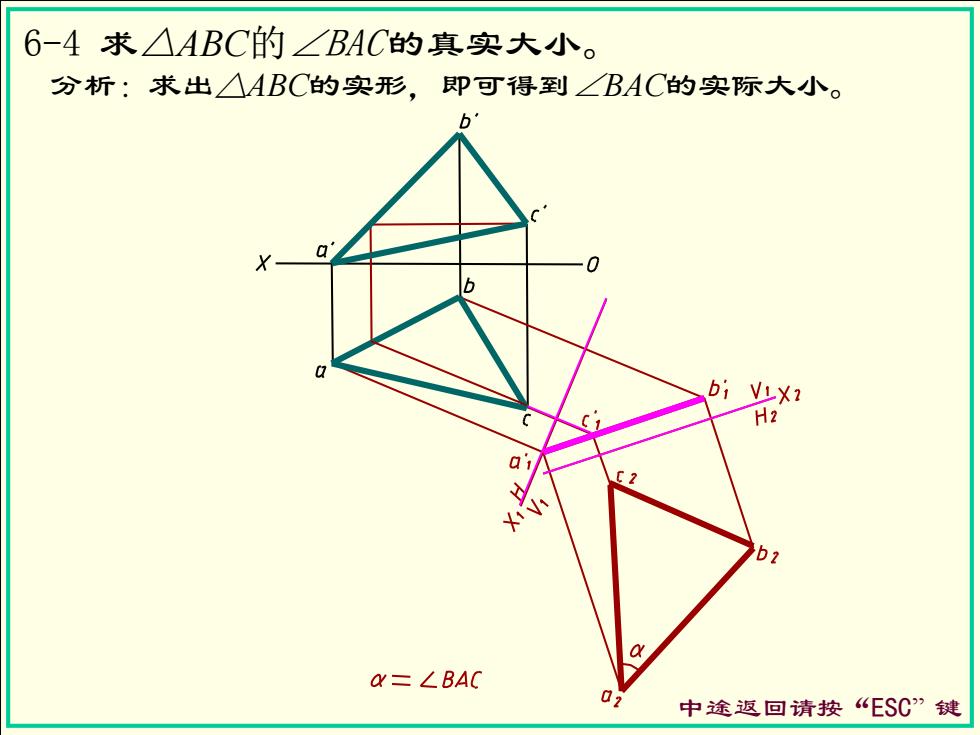
6-4求△ABC的∠BAC的真实大小。 分析:求出△ABC的实形,即可得到∠BAC的实际大小。 6 b bi VLX2 H2 b2 QX=∠BAC 中途返回请按“ESC”键
6-4 求△ABC的∠BAC的真实大小。 中途返回请按“ESC” 键 分析:求出△ABC的实形,即可得到∠BAC的实际大小
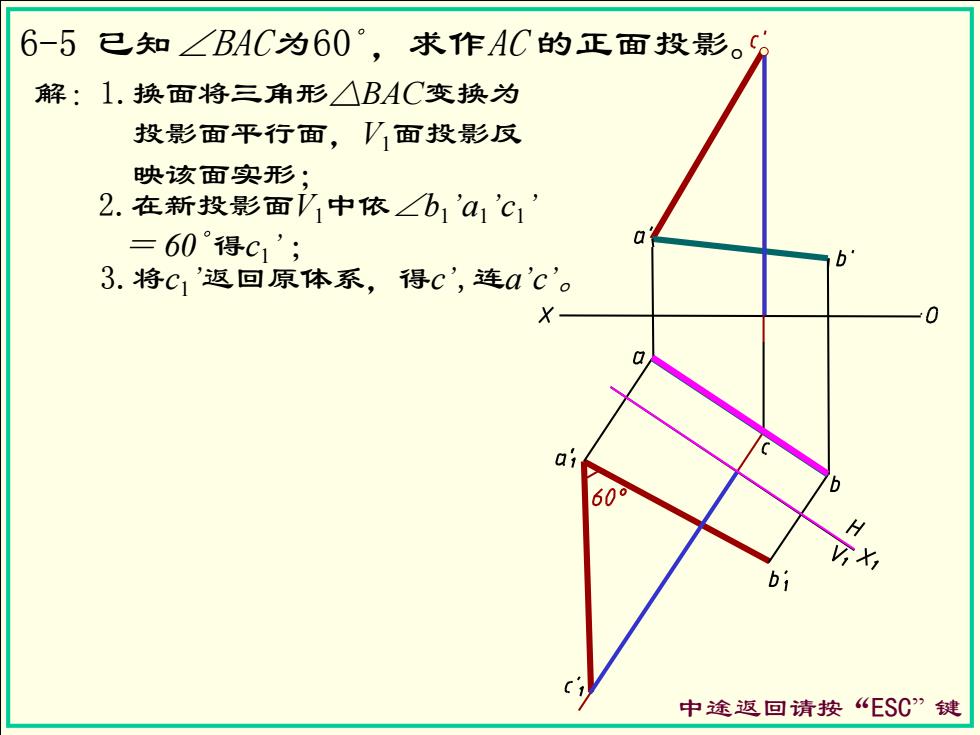
6-5已知∠BAC为60°,求作AC的正面投影。 解:1.换面将三角形△BAC变换为 投影面平行面,V面投影反 映该面实形; 2.在新投影面V1中依∠b1a1'c1 =60°得C1'; 3.将C1'返回原体系,得c',连a'c'。 0 ai 60 b 中途返回请按“ESC”键
6-5 已知∠BAC为60 ,求作AC 的正面投影。 中途返回请按“ESC” 键 解:1.换面将三角形△BAC变换为 投影面平行面,V1面投影反 映该面实形; 3.将c1 ’返回原体系,得c’,连a’c’。 2.在新投影面V1中依∠b1 ’a1 ’c1 ’ = 60 得c1 ’ ;

6-6已知点K到平面ABC的距离为15m,求作点K的水平 投影。 解:将△ABC变换成投影面垂直面a1b1'℃1’. 距面41'b,'℃1'15mm作平行线,按投影变换规律求出 k',由此求出水平投影k。 0 有两解 中途返回请按“ESC”键
6-6 已知点K 到平面ABC 的距离为15 mm ,求作点K 的水平 投影。 有两解 中途返回请按“ESC” 键 解:将△ABC变换成投影面垂直面a1 ’b1 ’c1 ’. 距面a1 ’b1 ’c1 ’15mm作平行线,按投影变换规律求出 k1 ’,由此求出水平投影k
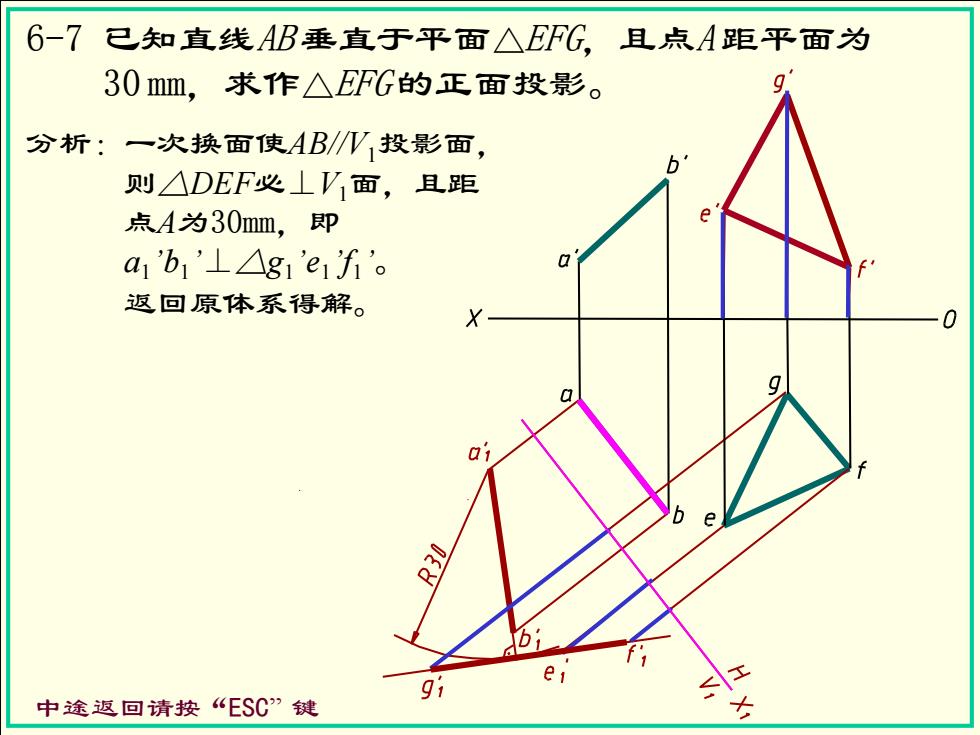
6-7已知直线AB垂直于平面△EFG,且点A距平面为 30mm,求作△EFG的正面投影。 分析:一次换面使ABW投影面, 则△DEF必⊥V,面,且距 点A为30mm,即 e a1'b1'⊥△g1'e1f。 返回原体系得解。 0 9 e e 中途返回请按“ESC”键
6-7 已知直线AB 垂直于平面△EFG,且点A 距平面为 30 mm,求作△EFG 的正面投影。 中途返回请按“ESC” 键 分析:一次换面使AB//V1投影面, 则△DEF必⊥V1面,且距 点A为30mm,即 a1 ’b1 ’⊥△g1 ’e1 ’f1 ’ 。 返回原体系得解
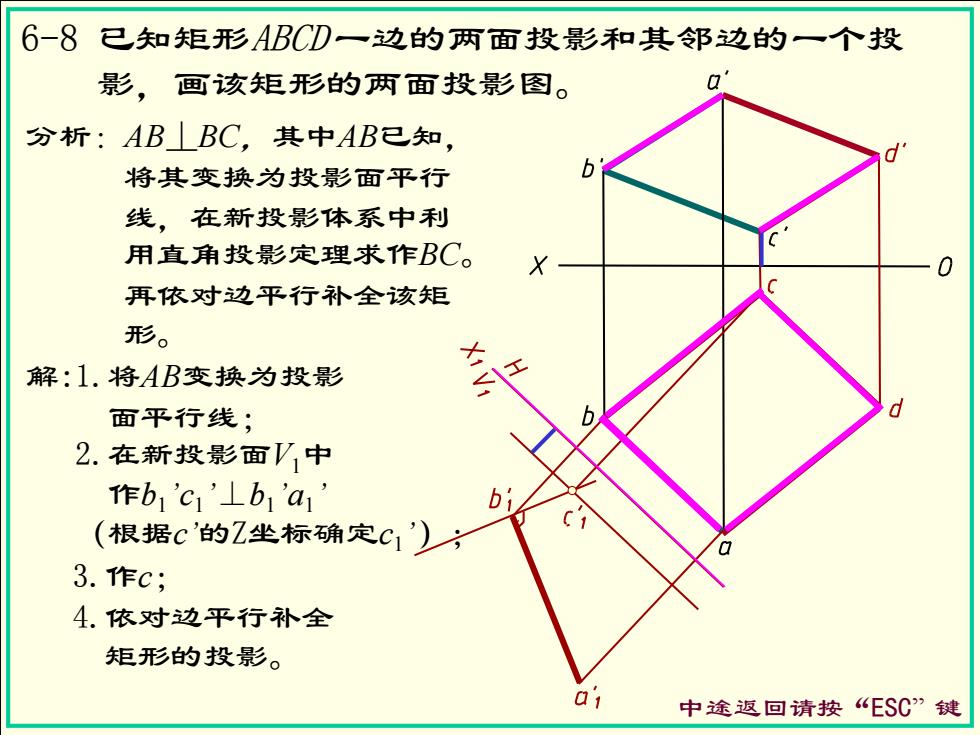
6-8已知矩形ABCD一边的两面投影和其邻边的一个投 影,画该矩形的两面投影图。 a 分析:AB⊥BC,其中AB已知, 将其变换为投影面平行 线,在新投影体系中利 用直角投影定理求作BC。 0 再依对边平行补全该矩 形。 解:1.将AB变换为投影 面平行线; 2.在新投影面V,中 作b1'C1'⊥b1'a1 bi (根据c'的Z坐标确定C1’) 3.作c; 4.依对边平行补全 矩形的投影。 01 中途返回请按“ESC”键
6-8 已知矩形ABCD 一边的两面投影和其邻边的一个投 影,画该矩形的两面投影图。 中途返回请按“ESC” 键 分析:AB⊥BC,其中AB已知, 将其变换为投影面平行 线,在新投影体系中利 用直角投影定理求作BC。 再依对边平行补全该矩 形。 解:1.将AB变换为投影 面平行线; 3.作c; 2.在新投影面V1中 作b1 ’c1 ’⊥b1 ’a1 ’ (根据c’的Z坐标确定c1 ’); 4.依对边平行补全 矩形的投影
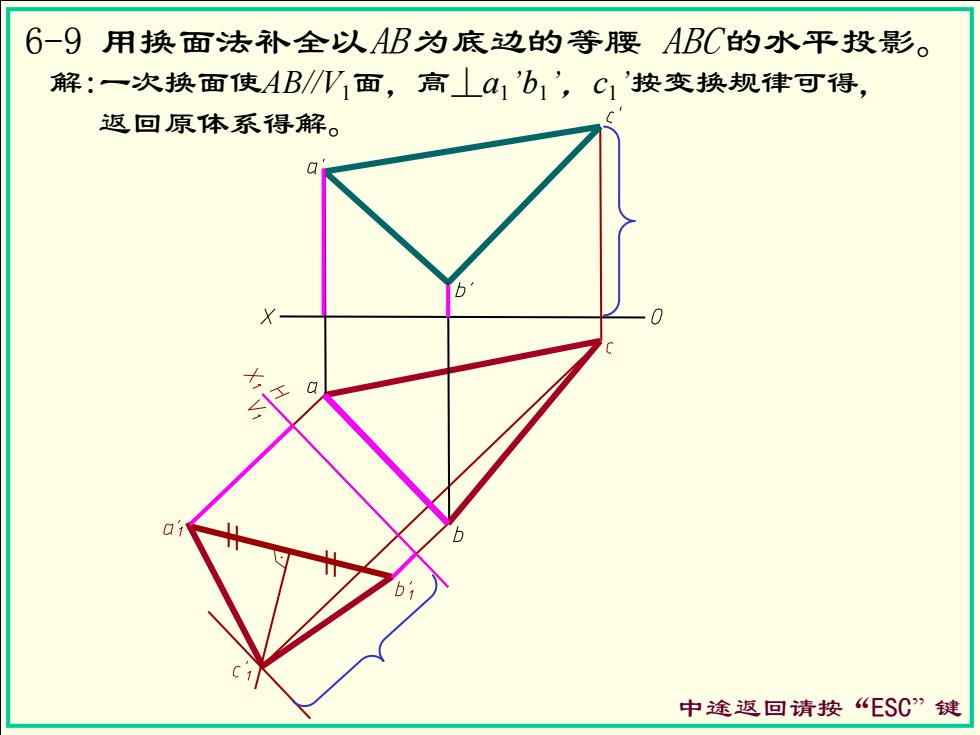
6-9用换面法补全以AB为底边的等腰ABC的水平投影。 解:一次换面使AB∥W面,高⊥41b1',C1'按变换规律可得, 返回原体系得解。 Q b 中途返回请按“ESC”键
6-9 用换面法补全以AB 为底边的等腰 ABC 的水平投影。 中途返回请按“ESC” 键 解:一次换面使AB//V1面,高⊥a1 ’b1 ’ ,c1 ’按变换规律可得, 返回原体系得解