Chemical Reaction Engineering 第六章混合过程与非理想反应器 6.1混合现象分类 按混合对象: •相同停留时间(年龄)物料之间的混合一同龄混合 •不同停留时间(年龄)物料之间的混合一返混 Batch Reactor CSTR
Chemical Reaction Engineering 第六章混合过程与非理想反应器 6.1混合现象分类 按混合对象: •相同停留时间(年龄)物料之间的混合—同龄混合 •不同停留时间(年龄)物料之间的混合—返混 Batch Reactor CSTR
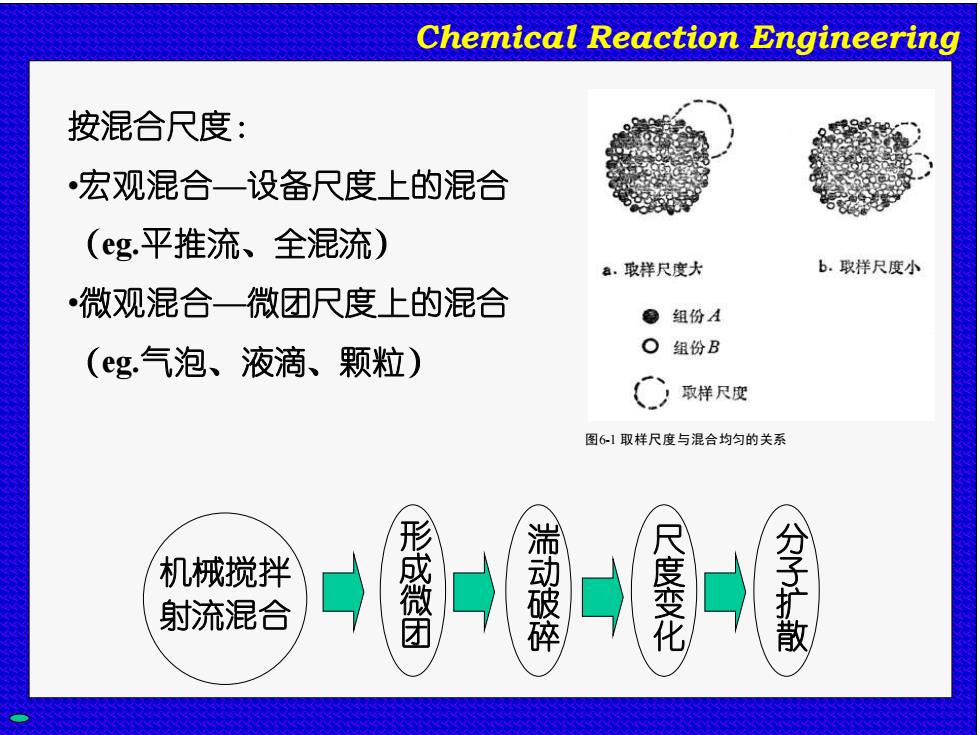
Chemical Reaction Engineering 按混合尺度: •宏观混合一设备尺度上的混合 (eg.平推流、全混流) a.取样尺度大 b.取样尺度小 ·微观混合一微团尺度上的混合 ●组份A (eg.气泡、液滴、颗粒) O组份B ) 取样尺度 图61取样尺度与混合均匀的关系 机械搅拌 射流混合 形成微团 满动破碎 尺度变化 分子扩散
Chemical Reaction Engineering 形 成 微 团 分 子 扩 散 湍 动 破 碎 尺 度 变 化 机械搅拌 射流混合 按混合尺度: •宏观混合—设备尺度上的混合 (eg.平推流、全混流) •微观混合—微团尺度上的混合 (eg.气泡、液滴、颗粒) 图6-1 取样尺度与混合均匀的关系

Chemical Reaction Engineering 6.2停留时间分布(RTD) Residence Time Distribution 一、 RTD概念 RTD一物料在反应器内(或出口)的停留时间分布 停留时间一物料质点的停留时间,是随机变量 处理方法一统计学,概率论方法 「几率一单个事件实验 概率实验 分率一大量事件实验(大数法则) 停留时间分布一年龄分布、寿命分布
Chemical Reaction Engineering 6.2 停留时间分布(RTD) Residence Time Distribution 一、RTD概念 RTD—物料在反应器内(或出口)的停留时间分布 停留时间—物料质点的停留时间,是随机变量 处理方法—统计学,概率论方法 概率实验 几率—单个事件实验 分率—大量事件实验(大数法则) 停留时间分布—年龄分布、寿命分布
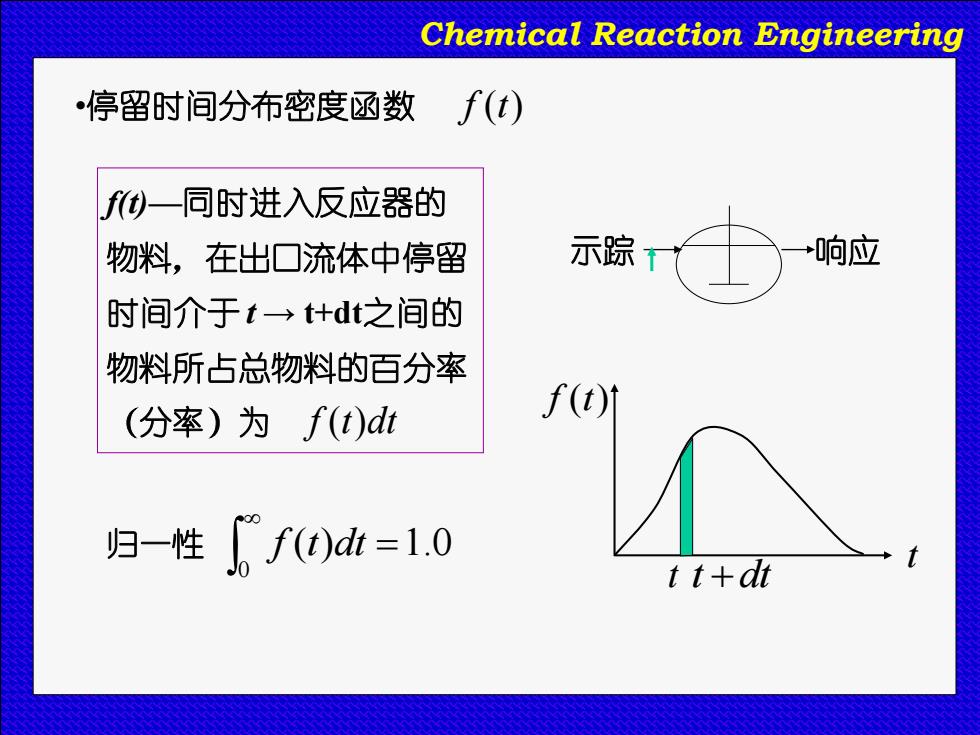
Chemical Reaction Engineering ·停留时间分布密度函数∫(t) f)一同时进入反应器的 物料,在出口流体中停留 示踪 响应 时间介于t→+dt之间的 物料所占总物料的百分率 (分率)为f(t)dt f(t)1 归-性广f)=1.0 t t+dt
Chemical Reaction Engineering f(t)—同时进入反应器的 物料,在出口流体中停留 时间介于 t → t+dt之间的 物料所占总物料的百分率 (分率)为 f (t)dt •停留时间分布密度函数 f (t) f (t) t t t +dt 归一性 = 0 f (t)dt 1.0 示踪 响应

Chemical Reaction Engineering ·停留时间分布(RTD)函数F(t) F(t)一停留时间分布函数 含义:同时进入反应器的物料,在出口流体中停留 时间小于t的物料所占总物料的百分率(分率)。 F(-[f(d= f(t)开 F(zt)=["f(t)dt=1-F(t) F(t) f0)= dF(t) dt 1.0 F()=f(t)dt=1.0
Chemical Reaction Engineering •停留时间分布(RTD)函数 F(t) F(t) —停留时间分布函数 含义:同时进入反应器的物料,在出口流体中停留 时间小于t 的物料所占总物料的百分率(分率)。 f (t) t t t 1.0 F(t) = = t F t f t dt 0 ( ) ( ) ( ) ( ) 1.0 0 = = F f t dt F( t) f (t)dt 1 F(t) t = = − ( ) dt dF t f t ( ) =

Chemical Reaction Engineering 二、 RTD的数字特征 数学期望t一RTD对原点的一阶矩(重心) 一意义:物料的平均停留时间 (t)dt [f(d -[Yadr f() 加权平均值 对PR、CSTR,等容时,7=VE Vo
Chemical Reaction Engineering 二、RTD的数字特征 •数学期望 t —RTD对原点的一阶矩(重心) —意义:物料的平均停留时间 = = 0 0 0 ( ) ( ) ( ) tf t dt f t dt tf t dt t 对PFR、CSTR,等容时, 0 v v t R = f (t) t 加权平均值 t

Chemical Reaction Engineering ·方差o?一RTD对数学期望的二阶炬 一意义:RTD对的偏离程度 -5a-iy f f() k- ffod f(t) 6-}≠0 有偏离 (-}=0无偏离 不同的分布一t接近
Chemical Reaction Engineering f (t) t t t −t − = 0 0 2 2 ( ) ( ) ( ) f t dt t t f t dt t ( ) ( ) 0 0 2 2 − = − t t t t 有偏离 无偏离 •方差 2 t —RTD对数学期望的二阶矩 —意义:RTD对 t 的偏离程度 f (t) t 不同的分布—t 接近

Chemical Reaction Engineering .-f0M f(d -f"(a-iYfO)dr =[(P-2t+i")f(O)dr -[Ef(Odi-2i[((dt+?["f()dr =[Pf(odi-22
Chemical Reaction Engineering 2 0 2 0 0 0 2 2 0 2 2 0 2 0 0 2 2 ( ) ( ) 2 ( ) ( ) ( 2 ) ( ) ( ) ( ) ( ) ( ) ( ) t f t dt t t f t dt t t f t dt t f t dt t tt t f t dt t t f t dt f t dt t t f t dt t = − = − + = − + = − − =

Chemical Reaction Engineering PFR(柱塞流,平推流): 0 t≠t f()= 00 t=1 0 F01 t<t t≥t 2=0 那么CSTR(全混流反应器)的RTD是如何的呢?
Chemical Reaction Engineering PFR(柱塞流,平推流): = = t t t t f t 0 ( ) = t t t t F t 1 0 ( ) 0 2 t = 那么CSTR(全混流反应器)的RTD是如何的呢? l=0 l=L

Chemical Reaction Engineering 三、停留时间分布的测定 示踪法一脉冲示踪法、阶跃示踪法 示踪剂一流动性相近、便于检测、惰性. A.咏冲法一测得停留时间分布密度函数 总量0=vC)dt 响应 在t→t+d的分率 f(t)dt=C()dt c(t) Q →f(t)= C(t) fcod tt+dt
Chemical Reaction Engineering 三、停留时间分布的测定 示踪法—脉冲示踪法、阶跃示踪法 示踪剂—流动性相近、便于检测、惰性. A.脉冲法—测得停留时间分布密度函数 c(t) t t t +dt 总量 = 0 Q vC(t)dt 响应 Q v Q vC t dt f t dt t t dt ( ) ( ) = 在 → + 的分率 = 0 ( ) ( ) ( ) C t dt C t f t