
历些毛子种枝大学 XIDIAN UNIVERSITY 键盘输入55,计算机怎么识别此数? 微机原理与系统设计 绪论 董明皓 dminghao@xidian.edu.cn
键盘输入55,计算机怎么识别此数? 微机原理与系统设计 绪论 董明皓 dminghao@xidian.edu.cn

历安毛子代枝大” 基础知识回顾 XIDIAN UNIVERSITY 位:bit,1个二进制位,0、1,计算机存储信息的最小单 元 ·字节:byte,8个二进制位,存储8个二进制数,0~255,- 128~127 字:word,16个二进制位,2个字节,存储16个二进制数 。 双字:double word,32个二进制位,4个字节,存储32个 二进制数 ·字长:基本数据单元所包含的二进制位数,8086-8/16。 存储器是按字节组织,即存储器存放的数位字节数 微机原理与系统设计 绪论 董明皓 dminghao@xidian.edu.cn
基础知识回顾 • 位:bit,1个二进制位,0、1,计算机存储信息的最小单 元 • 字节:byte,8个二进制位,存储8个二进制数,0~255,- 128~127 • 字:word,16个二进制位,2个字节,存储16个二进制数 • 双字:double word,32个二进制位,4个字节,存储32个 二进制数 • 字长:基本数据单元所包含的二进制位数,8086-8/16。 微机原理与系统设计 绪论 董明皓 dminghao@xidian.edu.cn 存储器是按字节组织,即存储器存放的数位字节数

历安毛子种枝大学 目录(2课时) XIDIAN UNIVERSITY 数制表示与转换 二进制数的运算规则 有符号数的表示 有符号数的运算及其溢出规则 BCD编码方法及其运算 ASCI编码方法 微机原理与系统设计 绪论 茧明皓 dminghao@xidian.edu.cn
1 数制表示与转换 2 二进制数的运算规则 3 有符号数的表示 4 有符号数的运算及其溢出规则 6 ASCII编码方法 5 BCD编码方法及其运算 微机原理与系统设计 绪论 董明皓 dminghao@xidian.edu.cn 目录(2课时)

历安毛子绑牧大学 1.1数制表示-常用表示法 XIDIAN UNIVERSITY 表征-Representation 常用数制:二、十、十六进制 ·二级制表示: 符号0、1集合,尾符B(Binary),110111B 、十进制表示: 符号0~9集合,尾符D(Decimal)或缺省,55D或55 。十六进制表示: 符号0~9、A~F集合,尾符H(Hexadecimal),37H 微机原理与系统设计 绪论 董明皓 dminghao@xidian.edu.cn
1.1数制表示-常用表示法 常用数制:二、十、十六进制 • 二级制表示: 符号 0、1 集合,尾符 B(Binary) , 110111B • 十进制表示: 符号 0 ~ 9 集合,尾符 D(Decimal) 或缺省,55D或55 • 十六进制表示: 符号 0 ~ 9、A ~ F 集合,尾符H(Hexadecimal) ,37H 微机原理与系统设计 绪论 董明皓 dminghao@xidian.edu.cn 表征-Representation

历些毛子种枝大” 1.1数制表示-常用表示法 XIDIAN UNIVERSITY 计算机中的数均用二进制表示(高低电平); 。 人们最熟悉、最常用的是十进制数; ·为书写方便,微机中的二进制数用十六进制数表 示; 微机原理与系统设计 绪论 茧明皓 dminghao@xidian.edu.cn
1.1数制表示-常用表示法 • 计算机中的数均用二进制表示(高低电平); • 人们最熟悉、最常用的是十进制数; • 为书写方便,微机中的二进制数用十六进制数表 示; 微机原理与系统设计 绪论 董明皓 dminghao@xidian.edu.cn
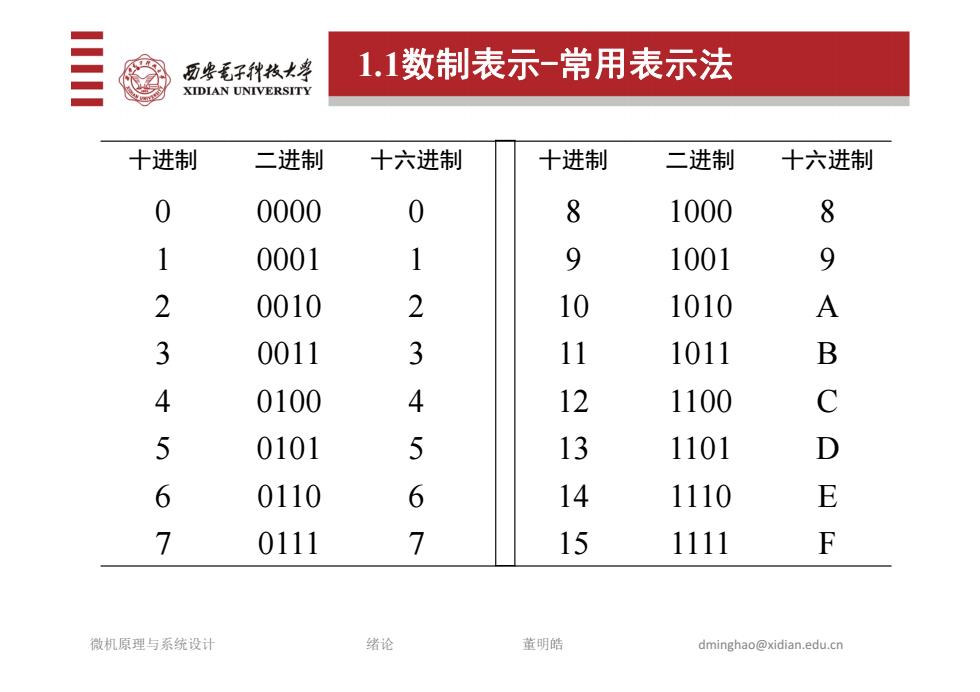
三 历些毛子种枝大” 1.1数制表示-常用表示法 XIDIAN UNIVERSITY 十进制 二进制 十六进制 十进制 二进制 十六进制 0 0000 0 8 1000 8 1 0001 1 9 1001 9 2 0010 2 10 1010 A 3 0011 3 11 1011 B 4 0100 4 12 1100 C 5 0101 5 13 1101 D 6 0110 6 14 1110 E 7 0111 7 15 1111 F 微机原理与系统设计 绪论 茧明皓 dminghao@xidian.edu.cn
十进制 二进制 十六进制 十进制 二进制 十六进制 0 0000 0 8 1000 8 1 0001 1 9 1001 9 2 0010 2 10 1010 A 3 0011 3 11 1011 B 4 0100 4 12 1100 C 5 0101 5 13 1101 D 6 0110 6 14 1110 E 7 0111 7 15 1111 F 1.1数制表示-常用表示法 微机原理与系统设计 绪论 董明皓 dminghao@xidian.edu.cn

历安毛子代枚大学 1.1数制表示-权值表示法 XIDIAN UNIVERSITY 任意一个数X可以表示成b进制数: X=∑k,b=kb”+.+kb-1+k。+kb+kb” b-基数;m-小数位的位数;n整数位的位数-1 255=2×102+5×10+5×100 369.2D=3×102+6×101+9×100+2×101 1010B=0X2+1X2+0×2+1X2+1X2 11010B=1×24+1X23+0×22+1×21+0×20 3C.4H=3×161+12×160+4×16-1 微机原理与系统设计 绪论 茧明皓 dminghao@xidian.edu.cn
任意一个数X可以表示成b进制数: n n m m n i m i k i k b k b k b k b 0 1 - 1 - 1 x b k b-基数;m-小数位的位数;n-整数位的位数-1 1.1数制表示-权值表示法 255 = 2×102 + 5×101 + 5×100 369.2D = 3×102 + 6×101 + 9×100 + 2×10-1 11010B 11010B = 1×24 + 1×23 + 0×22 + 1×21 + 0×20 11010B = 0×24 + 1×23 + 0×22 + 1×21 + 1×20 3C.4H = 3×161+12×160+4×16-1 微机原理与系统设计 绪论 董明皓 dminghao@xidian.edu.cn

历要毛子种枝大学 1.2数制转换-其他>十进制 XIDIAN UNIVERSITY 权值表示法 110111B=1×25+1×24+0×23+1×22+1×21+1×21 =32+16+0+4+2+1=55 3C.4H=3×16+12×16+4×16-1 =48+12+0.25=60.25/60.25D 微机原理与系统设计 绪论 董明皓 dminghao@xidian.edu.cn
1.2数制转换-其他十进制 权值表示法 110111B = 1×25 + 1×24 + 0×23 + 1×22 +1×21 + 1×21 =32 + 16 + 0 + 4 + 2 +1 = 55 3C.4H = 3×161+12×160+4×16-1 = 48 + 12 + 0.25 = 60.25/60.25D 微机原理与系统设计 绪论 董明皓 dminghao@xidian.edu.cn

历安毛子种枝大学 1.2数制转换-十进制→>其他(整数) XIDIAN UNIVERSITY (1)整数部分:除基取余法 例.十进制数55转换为十六进制数 转换过程如下: 低位 1655 16 余数为: 7= Ko t 1 . 0. .余数为: 3= K 高位 则:55=37H 十进制转其他进制,整数除基取余法,直至商为0,下高上低 微机原理与系统设计 绪论 董明皓 dminghao@xidian.edu.cn
(1)整数部分:除基取余法 16 3 .余数为:7= K0 16 0 .余数为:3= K1 16 55 转换过程如下: 低位 高位 1.2数制转换-十进制其他(整数) 例. 十进制数55转换为十六进制数 则:55 = 37H 十进制转其他进制,整数除基取余法,直至商为0,下高上低 微机原理与系统设计 绪论 董明皓 dminghao@xidian.edu.cn

历要毛子种枝大学 1.2数制转换-十进制→其他(整数) XIDIAN UNIVERSITY (1)整数部分: 除基取余法 例.十进制数55转换为二进制数 转换过程如下: 22 55 余数为: 1= 低位 示数为: 1= K 余数为: 1二 2222 2 .余数为: 0= 余数为: 1= .余数为: 1=K 高位 则: 55=110111B 十进制转其他进制,整数除基取余法,直至商为0,下高上低 微机原理与系统设计 绪论 董明皓 dminghao@xidian.edu.cn
2 55 2 27 .余数为:1= K0 2 13 .余数为:1= K1 2 6 .余数为:1= K2 2 3 .余数为:0= K3 2 1 .余数为:1= K4 2 0 .余数为:1=K5 低位 高位 1.2数制转换-十进制其他(整数) 例. 十进制数55转换为二进制数 转换过程如下: 则:55 = 110111B (1)整数部分:除基取余法 十进制转其他进制,整数除基取余法,直至商为0,下高上低 微机原理与系统设计 绪论 董明皓 dminghao@xidian.edu.cn