《高等数学》课程教学资源（课件讲稿）第十一章_11-3格林公式

第三节格林公式及其爱用 ·一、格林公式 ·二、年面上曲钱积分写路校无关的条件 ·三、二元西数的会微分求积 ·四、小结练习题

第三节 格林公式及其应用 • 一、格林公式 • 二、平面上曲线积分与路径无关的条件 • 三、二元函数的全微分求积 • 四、小结 练习题

一、格林公式 1、区域连通性的分类 设D为平面区域，如果D内任一闭曲线所围成 的部分都属于D,则称D为平面单连通区域，否 则称为复连通区域 单连通区域 复连通区域

一、格林公式 设D为平面区域, 如果D内任一闭曲线所围成 的部分都属于D, 则称D为平面单连通区域, 否 则称为复连通区域. 单连通区域 复连通区域 D D 1、区域连通性的分类

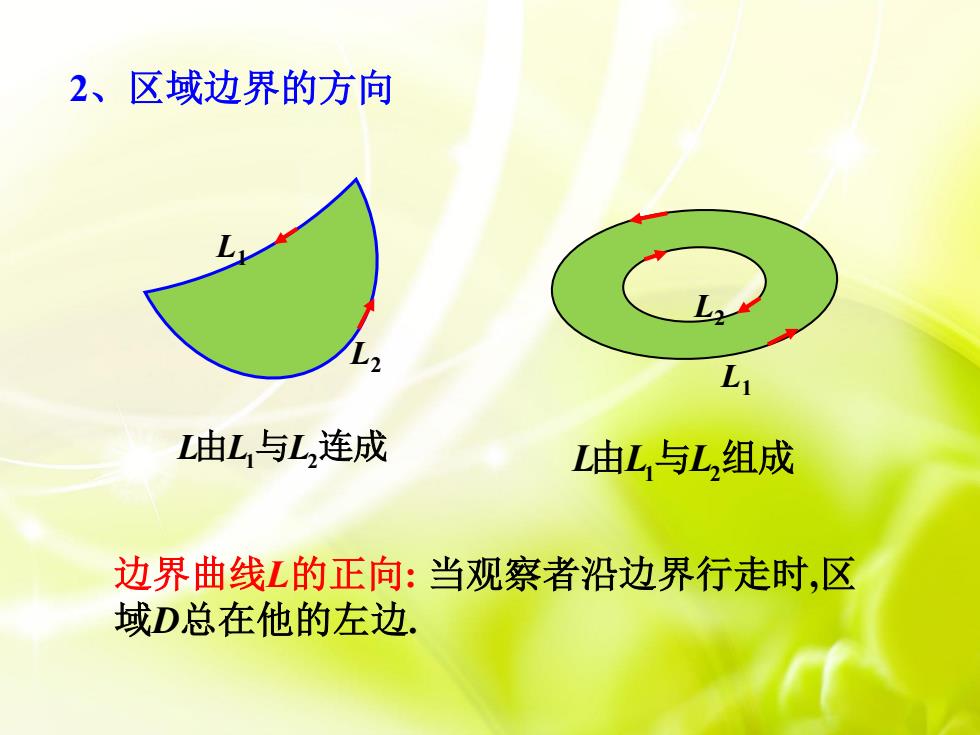
2、区域边界的方向 由L与L,连成 L由L,与L组成 边界曲线L的正向：当观察者沿边界行走时，区 域D总在他的左边

边界曲线L的正向: 当观察者沿边界行走时,区 域D总在他的左边. 2、区域边界的方向 L L L 由 1 2 与 组成 L2 L1 L L L 由 1 2 与 连成 L2 L1

3、格林公式 定理设闭区域D油分段光滑的曲线L围成， 函数P(x,Jy)及Q(x,y)在D上具有一阶连续的 偏导数，则有 那)d=∮.P+0 (1) 其中L是D的取正向的边界曲线. 公式(1)叫作格林公式. 注意：(1)P、Q在闭区域D上一阶偏导数的连续性； (2)曲线L是封闭的，并且取正向

3、格林公式 ( , ) ( , ) ( ) (1) . L D D L P x y Q x y D Q P dxdy Pdx Qdy x y L D          设闭区域 由分段光滑的曲线 围成， 函数 及 在 上具有一阶连续的 偏导数，则有 其中 是 的取正向的边界曲线 公式(1)叫作 定理 格林公式. 注意：(1) P、Q在闭区域D上一阶偏导数的连续性; (2) 曲线L是封闭的,并且取正向

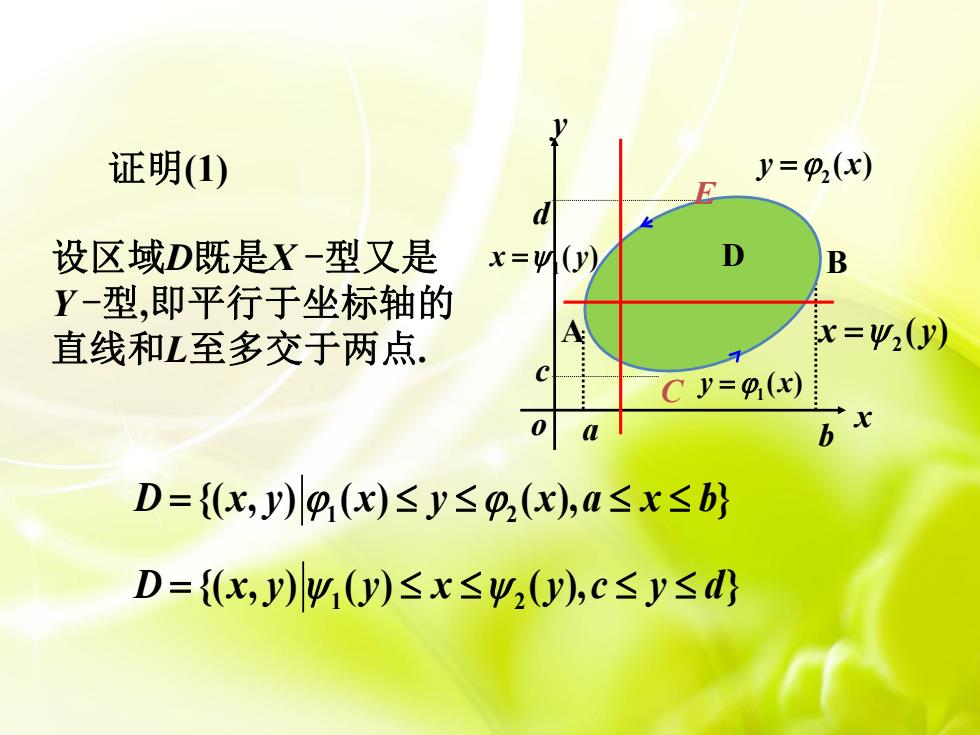
证明(1) y=0(x) 设区域D既是X-型又是 x=0y) B Y-型，即平行于坐标轴的 直线和L至多交于两点. x=42(0y) Cy=0(x) 0 b D={x,y)m,(x)≤y≤p(x,n≤x≤b} D={x,y)y)≤x≤2y),c≤y≤

1 2 D x y x y x a x b      {( , ) ( ) ( ), }   证明(1) 1 2 D x y y x y c y d      {( , ) ( ) ( ), }   y o x a b cd 1 y x   ( ) 2 y x   ( ) D A B C E 2 x y  ( ) 1 设区域D既是X -型又是 x y  ( ) Y - 型 ,即平行于坐标轴的 直线和 L至多交于两点

器- =0g,0wd-∫0g,0w) =∫ae(x,J4-厂e0(x,Jd -J+d A =∮ex,J x=420) 0 同理可正器=5严x临

D Q dxdy x   2 1 ( ( ), ) ( ( ), ) d d c c   Q y y dy Q y y dy     ( , ) ( , ) CBE CAE   Q x y dy Q x y dy   ( , ) ( , ) CBE EAC   Q x y dy Q x y dy   ( , ) L  Q x y dy  同理可证 ( , ) L D P dxdy P x y dx y       y x od 2 x y  ( ) D c CE 1 x y  ( ) B A 2 1 ( ) ( ) d y c y Q dy dx x      

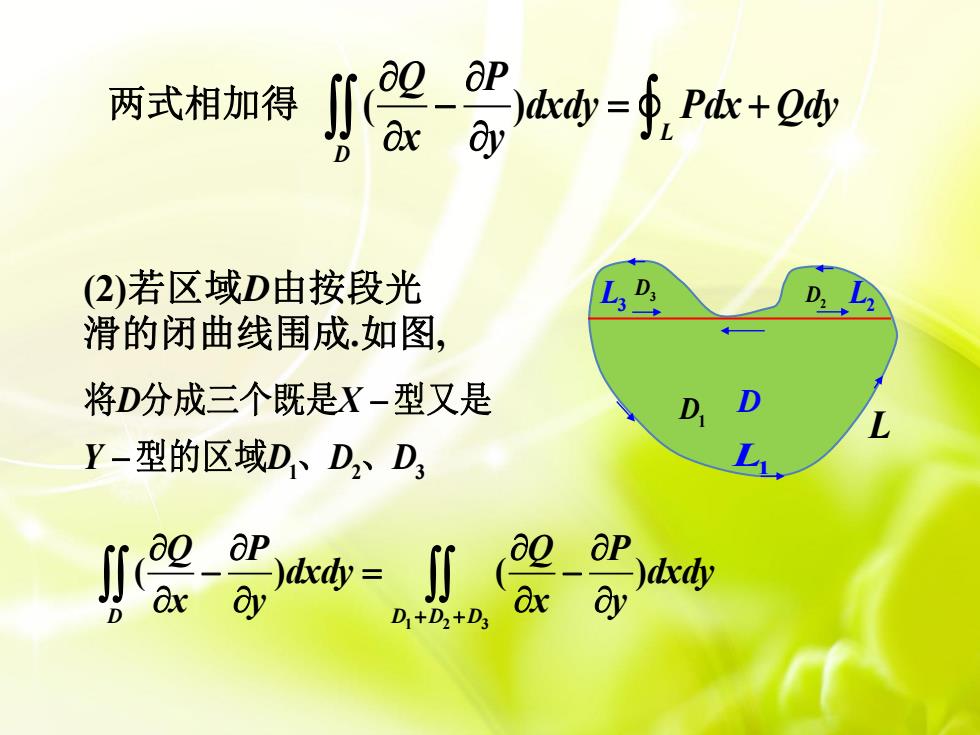
两式相加得 小架h-+ (2)若区域D由按段光 D 滑的闭曲线围成如图， 将D分成三个既是X-型又是 Y-型的区域DD2D3 小架器-儿是等a D1+D2+D3

L D (2)若区域D由按段光 滑的闭曲线围成.如图, L1 L3 L2 D1 D2 D3 两式相加得 ( ) L D Q P dxdy Pdx Qdy x y          1 2 3 ( ) ( ) D D D D Q P Q P dxdy dxdy x y x y                1 2 3 D X Y D D D   将 分成三个既是 型又是 型的区域 、

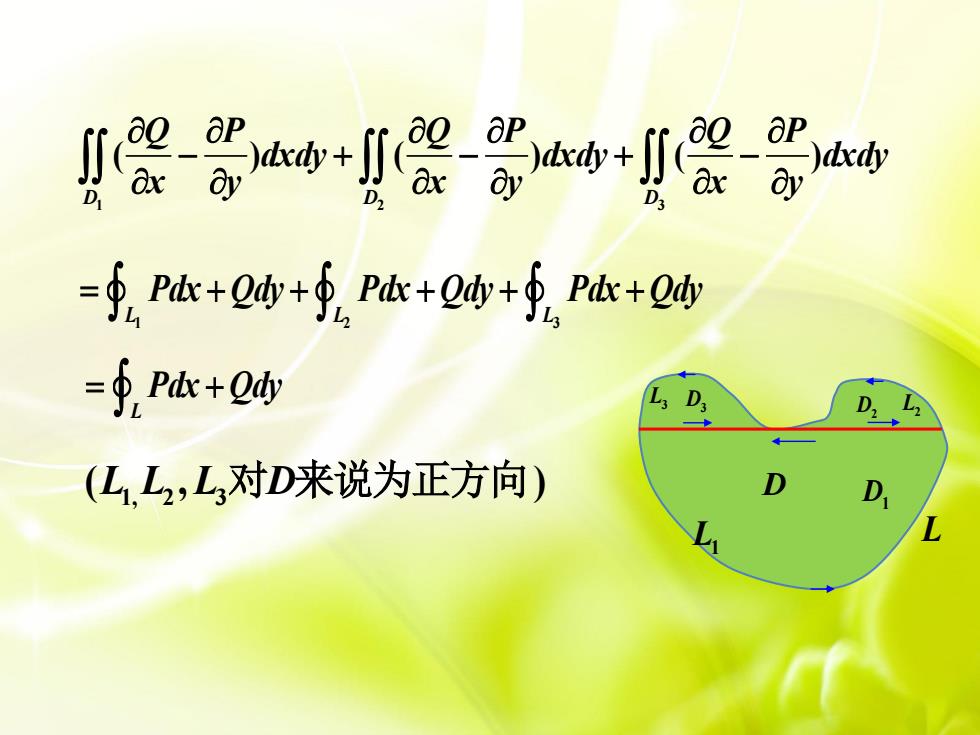
=∮P肱+Q+∮，P本+Q+∮P肱+O购 =∮Pt+Q (LL2,L对D来说为正方向)

1 2 3 ( ) ( ) ( ) D D D Q P Q P Q P dxdy dxdy dxdy x y x y x y                     L L L 1 2 3       Pdx Qdy Pdx Qdy Pdx Qdy    L   Pdx Qdy  1, 2 3 ( , ) L L L D 对 来说为正方向 L L1 L2 L3 D D1 D2 D3

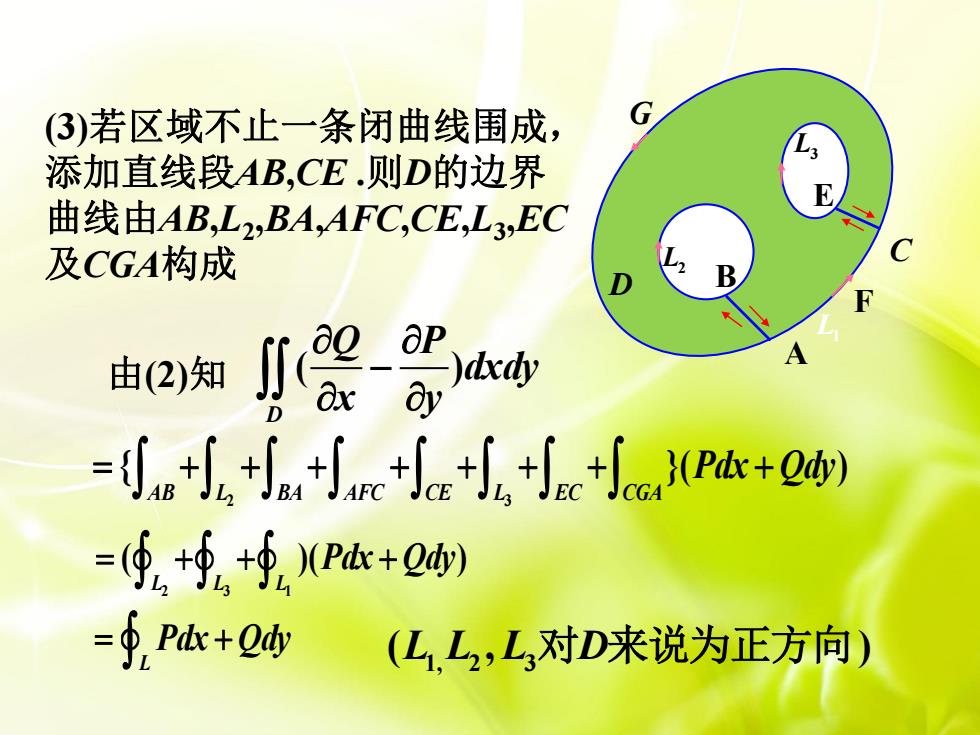
(3)若区域不止一条闭曲线围成， G 3 添加直线段AB,CE.则D的边界 E 曲线由AB,L2,BA,AFC,CE,L3,EC 及CGA构成 C F e斑r兴-Swa =可++∫4+m+etec+jcP+ =(⑨+∮+∮P肱+Q =∮Pt+ (LL2,L对D来说为正方向)

GD L 3 L 2 F C E L1 A B 由(2) 知 ( ) D Q P dxdy x y       2 3 { }( ) AB L BA AFC CE L EC CGA          Pdx Qdy         L   Pdx Qdy  2 3 1 ( )( ) LLL     Pdx Qdy  1, 2 3 ( , ) L L L D 对 来说为正方向 (3)若区域不止一条闭曲线围成， 添加直线段AB ,CE . 则 D的边界 曲线由AB , L 2 ,BA ,AFC,CE , L 3 ,EC 及CGA构成

4、简单应用 叮器器a-.体+Q财 (1).简化曲线积分 例1计算1=∮e'dc+(g3+xe-2y), 其中L为圆周x2+y2=2x的正向. 解P=e',2=y3+xe'-2y =e,00-ye ay Ox 80 OP ax ay 2=y 由格林公式有I=八yd=0

解 , y P  e Q xy xe y y 2 3    , y e y P    y y e x Q     3 3 y y P x Q       由格林公式有 ( ) L D Q P dxdy Pdx Qdy x y          3 d d D I y x y    2 . 1 例1 3 d ( 2 )d , y y L I e x xy xe y y     计算  其中L为圆周 x y 2x 2 2   的正向. O x y 0 (1). 简化曲线积分 4、简单应用